0 引 言
在海绵城市规划建设时,雨水径流总量控制是一个重要的控制指标。确定雨水径流流量,将为建设海绵城市提供科学的数据支持[1]。但由于雨水径流的流量不稳定,测量场地条件复杂多变等特点,使得雨水径流流量测量比较困难,因此研发雨水径流流量计量装置十分必要[2]。
目前量水设施主要有量水构筑物、量水仪表和堰槽三大类。量水构筑物一般应用于大流量的测量,对于测量小流量的雨水径流不适用。量水仪表对测量的水质要求较高,且雨水中的杂质会影响测量[3]。堰槽量水是一项较为古老的技术,应用广泛,其适应水流条件范围大,具有一定测流精度、耐久经济等特点。并且经过多年研究,堰槽量水的技术已经非常成熟[4-11]。在堰槽量水的方法中,巴歇尔槽对于施工的要求较高,施工的偏差会降低测量精度[12-13]。量水堰按出口的形状分为矩形堰、梯形堰和三角形堰,结构简单且流量的适应计量范围广,常用的为三角形堰。三角形堰又分为多种, 如三角形薄壁堰、三角形剖面堰等。对于一些流量小、水头低的流量测量常采用三角形薄壁堰进行测量[14]。
本研究设计的薄壁堰式智能流量监测装置基于三角形薄壁堰测量流量的原理,结合水位实时检测模块,进行流量测量。水位实时监测装置内置浮筒,将浮筒所受的浮力依据公式转化为水头高度,推算流量,精确可靠,并且结合物联网技术能将实时所测流量上传网站,可满足海绵城市建设中的小流量雨水的在线监测,为海绵城市规划提供科学数据。
1 装置设计原理
1.1 流量测量原理
流量测量是利用阿基米德原理,将1个标准尺寸的圆柱体浮筒连接力传感器,浮筒底端与堰口最底端平齐。当堰口出流时,浮筒会受到1个与堰口出流相同水位高度向上的浮力,力传感器可以测量出浮力大小,经过浮力公式计算转化为薄壁堰的上游水头高度,结合三角形薄壁堰公式,可计算出流量。原理如图1所示。
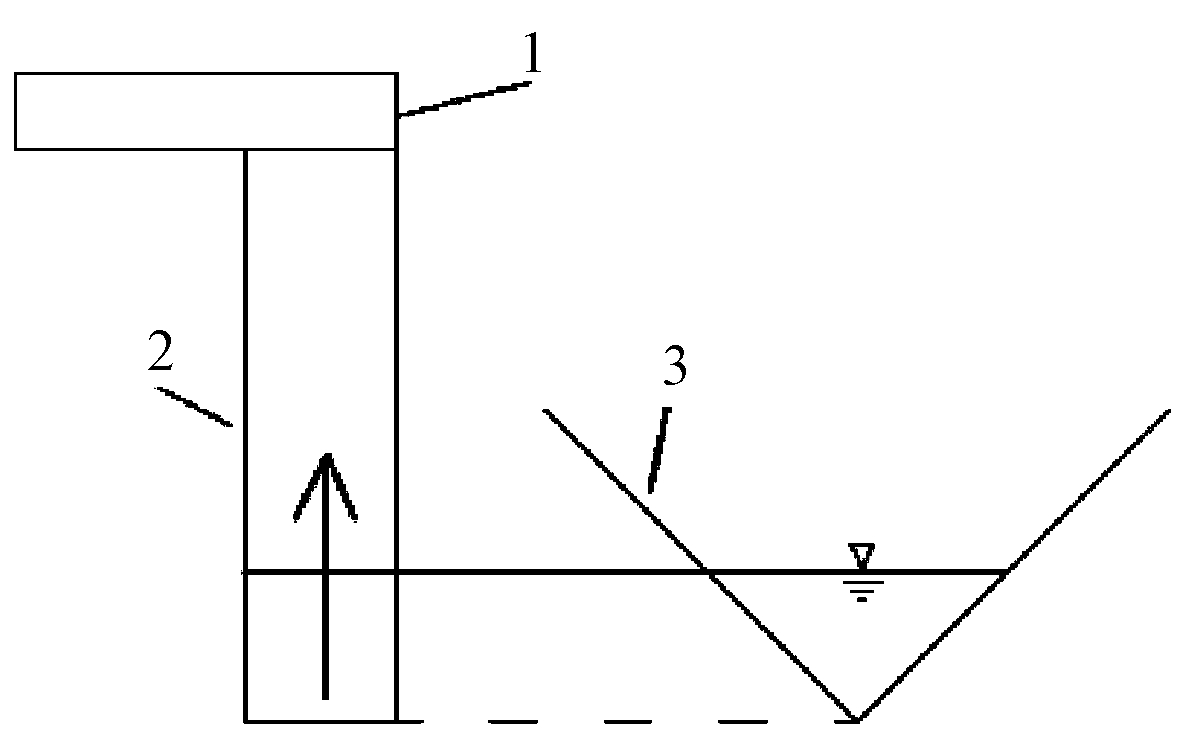
1—力传感器; 2—圆柱体浮筒; 3—三角形薄壁堰。
图1 流量测量原理示意
Fig.1 Design principle for the flow rate measurement
三角形薄壁堰的流量公式如式(1)所示:
式中:Q为流量,m3/s;C为流量系数;θ为三角形缺口角度,(°);g为重力加速度,9.8 m/s2;he为上游水头,m。
当θ=90°时,可将式(1)简化为经验公式:
可以明显看出:式(2)反映的是上游水头he和流量Q之间的函数关系,即Q=f(he)。若已知上游水头he,则可求出对应的流量Q。
浮力公式如式(3)所示:
P=ρgShe
(3)
式中:P为压力,Pa;ρ为水密度,kg/m3;g为重力加速度,9.8 m/s2;S为圆筒底面积,m2;he为上游水头,m。
根据式(3),可将测得的压力P数值转化为上游水头he,再结合式(1),可推导出压力P与流量Q的函数关系式,即:
通过测量压力P值,可计算出流量Q,满足Q=f(P)。将每个时刻的流量Q进行积分,可得到总流量Q总,即:
Q总![]()
上述推导建立了三角形薄壁堰流量Q与压力P之间的函数关系。
1.2 装置设计
薄壁堰式智能流量监测装置主要由2部分组成(图2),分别是三角形薄壁堰和水位实时监测模块。三角形薄壁堰参照行业标准JJG(水利)004—2015《明渠堰槽流量计计量检定规程》[15]的要求制作。整个堰槽采用不锈钢金属制作,以保证堰的强度和表面光滑。三角形薄壁堰制作尺寸为堰板厚1 mm,底边长550 mm,高250 mm。堰开孔角度为90°,堰口宽度为400 mm,堰口垂直高度为190 mm。采用矩形渠道进水,保持水流稳定。在矩形渠道旁边外接1个方形盒子,作为静水井。静水井底部与矩形渠道连通,以保证静水井内水位与矩形渠道水位一致,静水井用于安放水位实时监测模块,并可消除水流扰动带来的测量值波动。
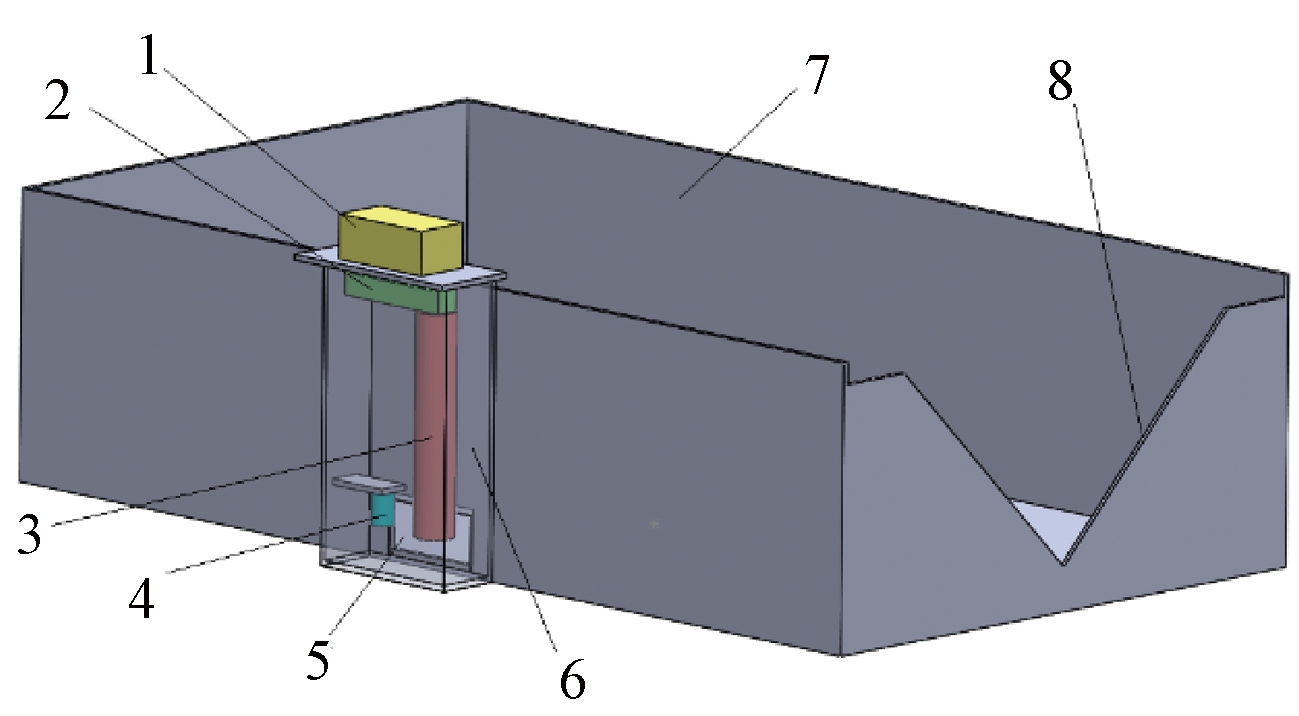
1—通信部分; 2—力传感器; 3—圆柱体浮筒; 4—浮球阀;5—连通孔; 6—静水井; 7—堰箱; 8—堰口。
图2 薄壁堰式智能流量监测装置示意
Fig.2 Structure of the thin-wall weir intelligent measure and control system
水位实时监测模块整体尺寸略小于方形静水井,可以方便放入静水井中进行固定。水位实时监测模块主要由启动部分、力传感器部分和通信部分组成。启动部分为浮球阀,浮球阀高度与堰口底端平齐,当水位达到堰口出流时,浮球阀开启,将装置激活。力传感器位置高于堰口,防止水位过高影响测量。力传感器一端固定在平板上,另一端接有1个直径为75 mm的圆柱体浮筒,浮筒长度大于堰口的整体高度,浮筒的底端与堰口底部平齐,保证测量的液位高度为堰的上游水头高度。通信部分位于平板上方,保证信号不被遮挡,传输稳定。通信部分将力传感器测得的数据传输到网站,并且接收网站的指令,双向交互,实现实时在线监测。通信部分在日常情况下将设备处于待机状态,节省电力。当水位高于堰口发生出流时,浮球阀开启,通信部分接收到开启信号,将装置激活进行流量监测,并将数据实时传输到网站。当水位低于堰口时,浮球阀关闭,通信部分重新回到待机状态。
2 流量率定实验
为验证三角形薄壁堰的实际测量值的准确性,在实验室对该装置进行了实际流量率定实验,率定实验装置如图3所示。
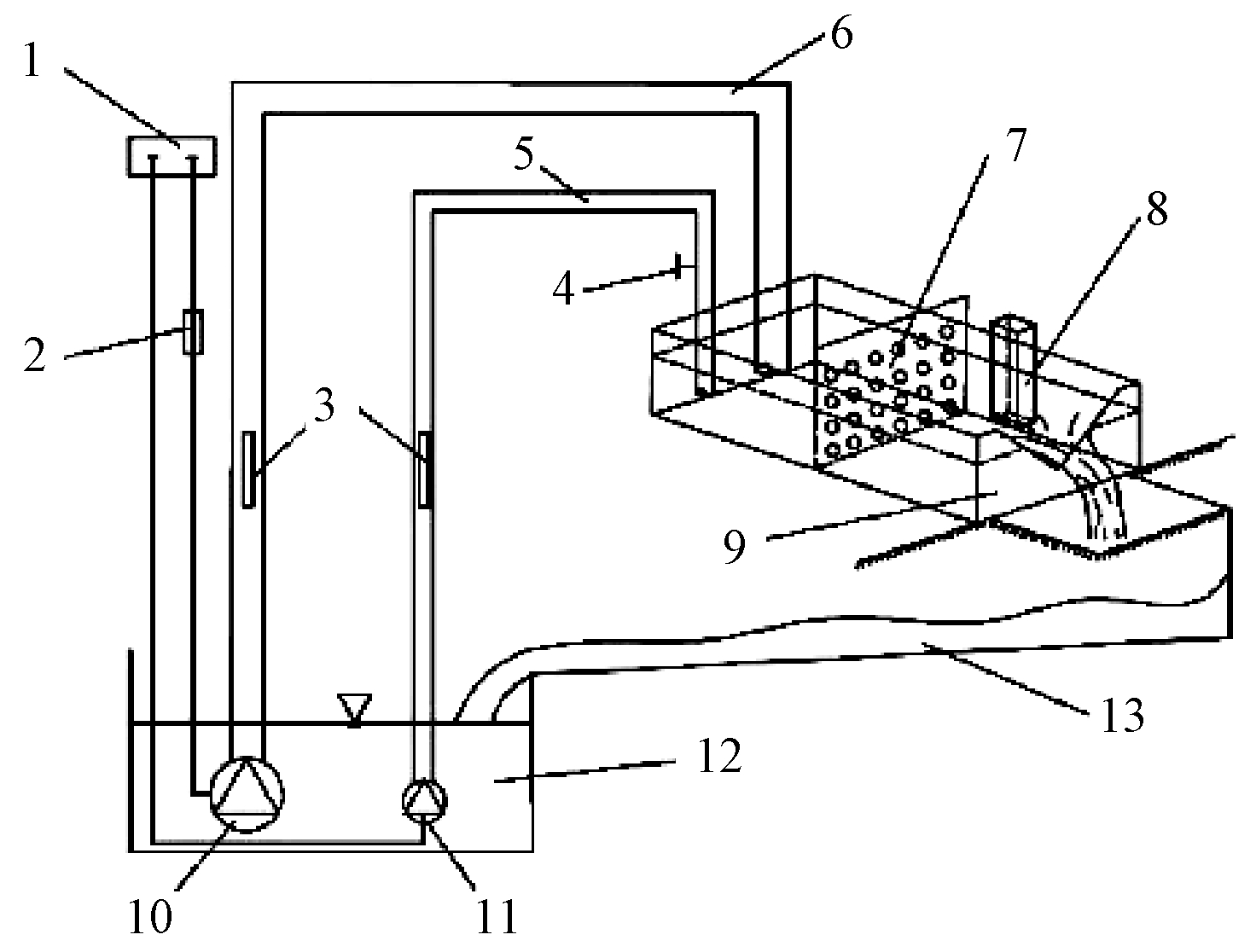
1—电源; 2—变频器; 3—超声波流量计; 4—球阀; 5—63 mm PVC管; 6—110 mm PVC管; 7—多孔稳流板; 8—静水井; 9—三角形薄壁堰;10—大潜水泵; 11—小潜水泵; 12—地下水库; 13—渠道。
图3 实际流量率定实验装置
Fig.3 Device for flow rate calibration experiments
在实验过程中,由于水泵的量程范围有限,故使用一大一小2台潜水泵对装置进行供水。在使用较小流量时用小潜水泵供水,小潜水泵最大流量为3.5 L/s。在使用较大流量时用大潜水泵供水,大潜水泵最大流量可以满足实验流量上限。小潜水泵接连1根直径为63 mm的PVC管,使用球阀控制出水流量。大潜水泵连接1根直径为110 mm的PVC管,使用变频器控制水泵转速,调节出水流量。使用超声波流量计计量的流量为真实流量,将超声波流量计安装在管道的上升段,确保管道内为满管流,保证计量的准确性。在管道出口处,放置多孔稳流板来削减水流的波动,稳定水流。在静水井处安装水位实时监测模块,记录被测流量水位。打开水泵调节好流量后,每次记录时让水流在整个装置内运行10~15 min,以减小计量误差。水流通过装置跌入渠道内,保证堰口处自由出流不被水位淹没。水流经渠道流入地下水库,实现循环供水。
3 率定结果与分析
3.1 率定实验结果
在率定实验中,由于直接使用水泵供水,使实测数据具有一定的离散性,故需采集多组数据,并求其平均数消除误差。在实验中,将超声波流量计的电流转化成电压,采用DC电压记录器每隔0.1 s采集1次数值。水流稳定后,选取一段时间内所有数据的平均值记为实际流量。
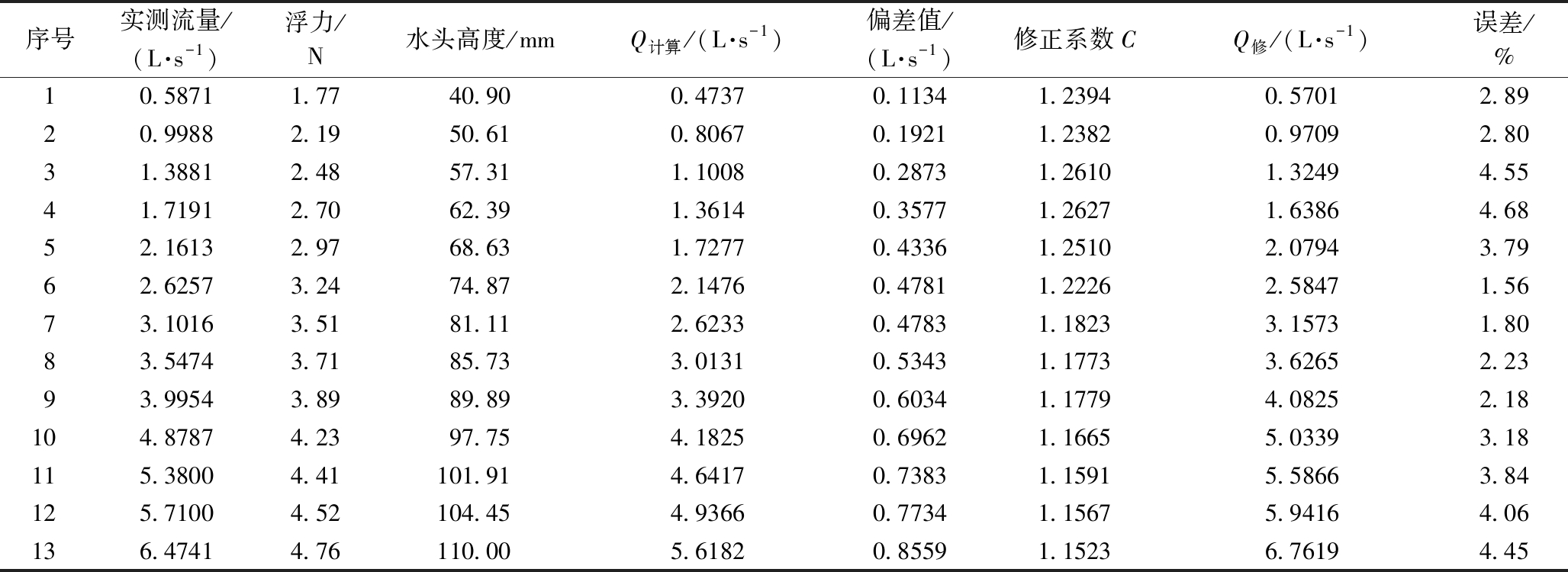
实验分2组进行,分别记录了小泵和大泵不同情况下的流量数值,其中小泵8组,大泵5组。用超声波流量计测得的流量范围为0.5871~6.4741 L/s。测量数据包括实测流量、浮筒所受浮力,具体数据如表1所示。
由表1可看出:实测流量与通过浮力转化计算的流量具有一定的偏差,并且偏差随着流量的增大而增大。将偏差值与浮力进行线性拟合,如图4所示。可知:浮力与偏差值之间满足一次函数关系,如式(6)所示。
Y=0.2385X-0.311
(6)
表1 不同条件下泵的流量实验数据
Table 1 Experimental data of pump flow under different work comdition
序号实测流量/(L·s-1)浮力/N水头高度/mmQ计算/(L·s-1)偏差值/(L·s-1)修正系数CQ修/(L·s-1)误差/%10.58711.7740.90 0.4737 0.1134 1.2394 0.5701 2.89 20.99882.1950.61 0.8067 0.1921 1.2382 0.9709 2.80 31.38812.4857.31 1.1008 0.2873 1.2610 1.3249 4.55 41.71912.7062.39 1.3614 0.3577 1.2627 1.6386 4.68 52.16132.9768.63 1.7277 0.4336 1.2510 2.0794 3.79 62.62573.2474.87 2.1476 0.4781 1.2226 2.5847 1.56 73.10163.5181.11 2.6233 0.4783 1.1823 3.1573 1.80 83.54743.7185.73 3.0131 0.5343 1.1773 3.6265 2.23 93.99543.8989.89 3.3920 0.6034 1.1779 4.0825 2.18 104.87874.2397.75 4.1825 0.6962 1.1665 5.0339 3.18 115.38004.41101.91 4.6417 0.7383 1.1591 5.5866 3.84 125.71004.52104.45 4.9366 0.7734 1.1567 5.9416 4.06 136.47414.76110.00 5.6182 0.8559 1.1523 6.7619 4.45
注:1~8为小泵组; 9~13为大泵组;水头高度、Q计算与Q修分别由式(3),(2),(7)计算得出。

![]() 偏差值; ——拟合曲线。
偏差值; ——拟合曲线。
图4 实测流量与浮力转化计算流量的偏差值与浮力的拟合曲线
Fig.4 Formula fitting results of buoyantcy, and D-value between measured flow values and the calculated values
将实测流量与计算流量进行求商计算,得到修正系数C。修正系数C平均值为1.2036,方差R2=0.9983。即实测流量与计算流量之间存在比例关系,Q实测=MQ计算,系数M=1.2036。将式(2)进行修正,修正后新流量如式(7)所示:
通过式(7)计算得到修正后流量。将修正后流量与实测流量进行误差计算如式(8)所示,得出所有误差值均<4.7%。当流量为2.5~3 L/s时误差<2%,流量偏大或偏小误差均较大。实验数据表明,该装置具有良好的测量效果。
误差![]()
3.2 误差分析
由实验数据可以看出,流量小时,修正系数C偏差较大。随着流量逐渐变大,修正系数C越来越小。造成这一现象的原因主要有两点:一是由堰流基本特点决定的,流量小时,水流受表面张力的影响较大。二是因为小流量下管道流速分布不均匀,实验使用超声波流量计计量管道流量误差较大。
4 应用案例
某园区为海绵城市试点工程,在海绵城市建设中,需要计量雨水经屋顶流入绿化带的流量。按照文献[15]的要求,将装置水平安放在混凝土基座上。堰口距下游尾水≥0.1 m。由于雨落管动能较大,故在雨落管出口处对雨落管的水流进行消能处理。屋顶为铁皮屋顶,因此水中不含泥沙碎石和漂浮物,水质较为清洁。
对该地区2018年8月20日的降雨进行监测,装置完整地记录了整个降雨过程中雨水径流的变化,并将信息传送到网站。降雨流量监测界面如图5所示。可知:降雨初期,流量随着降雨的进行而逐渐变大。经历一段时间后,流量达到峰值,随后流量减小,最终趋于0。整个过程中,流量计有效记录了降雨屋顶流量的过程,故该方法在流量计量领域有良好的适用性。
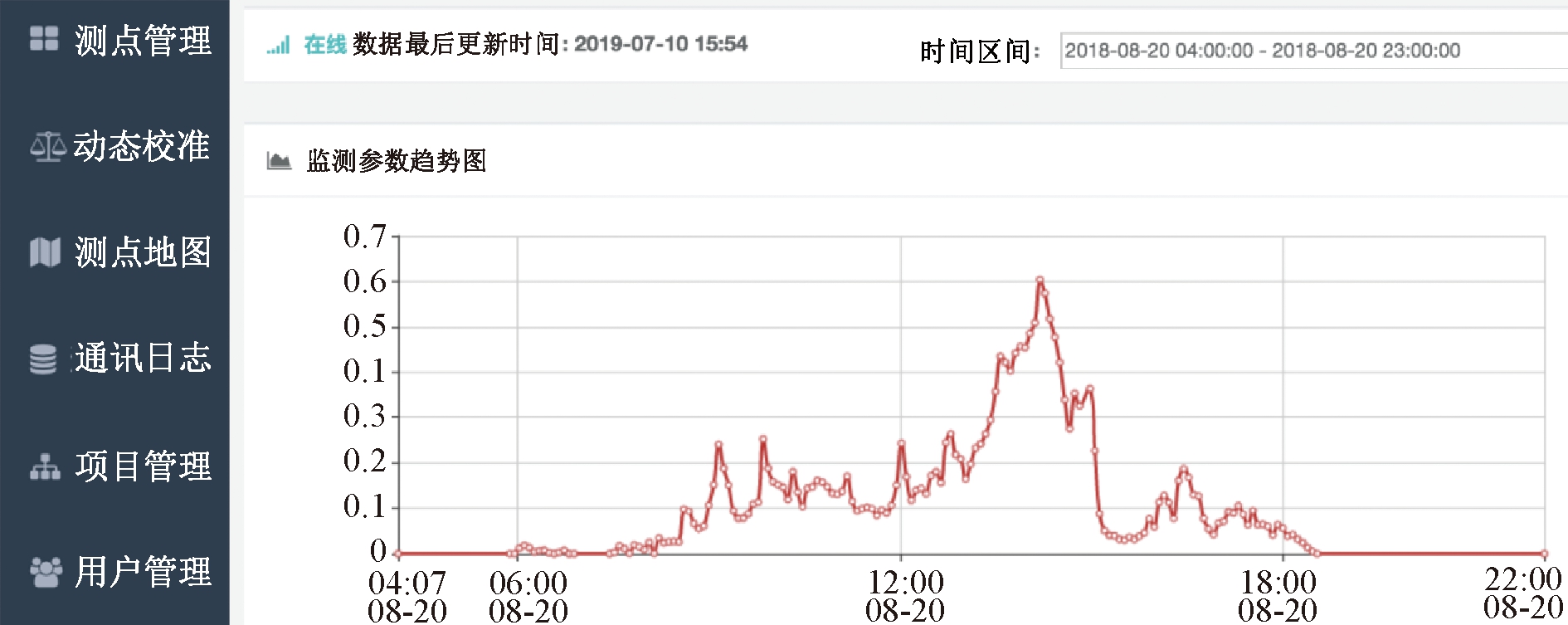
图5 降雨流量监测界面
Fig.5 The work interface of rainwater runoff monitoring
5 结束语
薄壁堰式智能流量监测装置基于三角形薄壁堰测量流量的原理,具有简便、可靠和精确的特点。与量水构筑物和量水仪表相比较,三角形薄壁堰更适合进行雨水径流流量测量。
通过测量浮筒的浮力进而转化为上游水头来计算流量,是一种十分有效的雨水径流测量方法。经过水力特性的率定实验,其模型计算流量与实测流量基本一致,误差<4.7%,精确度良好。特别针对水头低,流量小的明渠流流量具有较好的测量效果。
作为一种新型的流量监测装置,该流量计可以实现在线精确测量雨水流量,误差小,实时性强,在服务科研工作和实际工程中,均具有较高的应用和推广价值。
[1] 王文亮, 李俊奇, 车伍, 等. 雨水径流总量控制目标确定与落地的若干问题探讨[J]. 给水排水, 2016, 52(10):61-69.
[2] 田欢, 王文海, 李芸, 等. 巴歇尔槽测量雨水径流流量方法及其改进研究[J]. 环境监测管理与技术, 2016,28(6):9-13.
[3] 甄晶博, 吕宏兴, 彭向岐,等. 水头可调薄壁堰式渠道流量智能测控系统研究[J]. 节水灌溉, 2014,28(6):89-92.
[4] 王长德. 量水技术与设施[M]. 北京:中国水利水电出版社, 2006.
[5] 田欢, 王文海, 李芸,等. 雨水明渠流量测量常用设备及其选型[J]. 环境与可持续发展, 2016, 41(2):60-63.
[6] Samani Z. Three simple flumes for flow measurement in open channels[J]. Journal of Irrigation & Drainage Engineering,2017,143(6): 04017010.
[7] 白静,谢崇宝,黄斌,等.基于水动力学模型的灌溉渠道水流量水方法研究[J].中国农村水利水电,2019(3):119-121,126.
[8] Yeung H. An examination of BS3680 4C (ISO/DIS 4369) on the measurement of liquid flow in open channels flumes[J]. Flow Measurement and Instrumentation, 2007, 18(3/4):175-182.
[9] Azimi H, Bonakdari H, Ebtehaj I. Sensitivity analysis of the factors affecting the discharge capacity of side weirs in trapezoidal channels using extreme learning machines[J]. Flow Measurement and Instrumentation, 2017, 54:216-223.
[10] 曹湧. 明渠流量测量系统的研究与开发[D]. 合肥:合肥工业大学, 2002.
[11] 严晓军. 我国灌区量水技术现状及发展趋势[J]. 中国科技信息, 2010(17):89-90.
[12] 杨林胜. 浅谈巴歇尔量水槽及其设计参数确定的一般方法[J]. 甘肃农业, 2010(9):74-75.
[13] 李杰, 吕宏兴, 胥维纤. 巴歇尔量水槽水力特性试验研究[J]. 节水灌溉, 2009(12):45-47.
[14] 杨琳, 黎裕文, 张文涛. 三角形薄壁堰流量测验方法在山溪性小河中的应用[J]. 人民珠江, 2008, 29(3):65-67.
[15] 中华人民共和国水利部. 明渠堰槽流量计计量检定规程:JJG(水利)004—2015[S].北京:中国水利水电出版社.