0 引 言
水源地安全问题日益引起国内外的重视。水源水质风险除了面源、点源污染外,还存在突发水污染事件的可能。以长江下游为例,目前其拥有化学工业园区、新材料工业园区和现代物流园区等一批工业基地,此外,每年进出沿江各港口危险货物船舶超过6万艘次,年吞吐量超过8000万t[1],一旦发生事故,沿江城市水源地将受到严重威胁,所产生的供水危机后果难以估量。
自来水公司对水源水质安全风险建立应急预案,一般采取对污染原水在进厂前预处理、进厂后强化处理或启用备用水源等措施。但直接在水源地取水的水厂往往在发现事故时污染物已经进厂,不能及时应对,造成供水事故。因此预警时间非常关键。建设前置调蓄池,延缓污染水体进厂时间,给应急处置留出空间,是解决突发水污染事件的创新性举措。
在确定前置调蓄设计参数方面,目前无成熟的技术可直接利用,只能根据流速估算预警时间,不够精确。而水环境数值模拟可以对污染物在水力、化学、生物和气候等因素的作用下随时间和空间的迁移转化过程及其规律进行准确的描述[2]。代表性水质模型有WASP和EFDC等。EFDC在水动力学计算方面具有突出优势的三维数模,可精确模拟出动态的一维、二维、三维水流条件污染物迁移变化规律。
本文以镇江市自来水公司水源安全保障工程前置调蓄池为对象,采用EFDC水环境模拟软件,开展水动力与污染物扩散数值模拟,预测了不同工况下污染物进入调蓄池后的变化状态、到达取水口时间及影响因素,为管理者处理水源突发水污染事件提供技术支撑,研究结果对同类工程设计具有参考价值。
1 前置调蓄池概况
镇江市水源安全保障工程前置调蓄池位于征润洲水源地一级保护区内,总库容为30万m3,设计取水规模为60万m3/d,全长为1800 m。主要由长江进水涵闸、长江取水泵房、原水前置调蓄池、配套原水检测系统、应急处置系统和导试水厂等项目组成。调蓄池绝大部分为土底土边坡,前端衬砌混凝土方砖,中间设置钢筋混凝土方形桥柱加橡胶膜组合建成导流墙,将调蓄池分为2个廊道[3]。具体几何尺寸如表1所示。
表1 调蓄池设计参数
Table 1 Design parameters of the storage basin

总库容/万m3取水规模/(万m3·d-1)斜壁坡度池底平均标高/m设计水位标高/m调蓄池前端长度/m第1廊道长度/m第2廊道长度/m平均流速/(m·s-1)30601∶2.5-1.93.51008009000.03~0.05
长江原水经取水涵闸和取水泵房,从调蓄池东北角进水口进入调蓄池。原水沿导流墙先向西南方向经第1廊道流动,再向东北方向经第2廊道流动,最后由出水口流出,由设置在调蓄池东南角的取水泵站输送到金山和金西水厂[3],如图1所示。
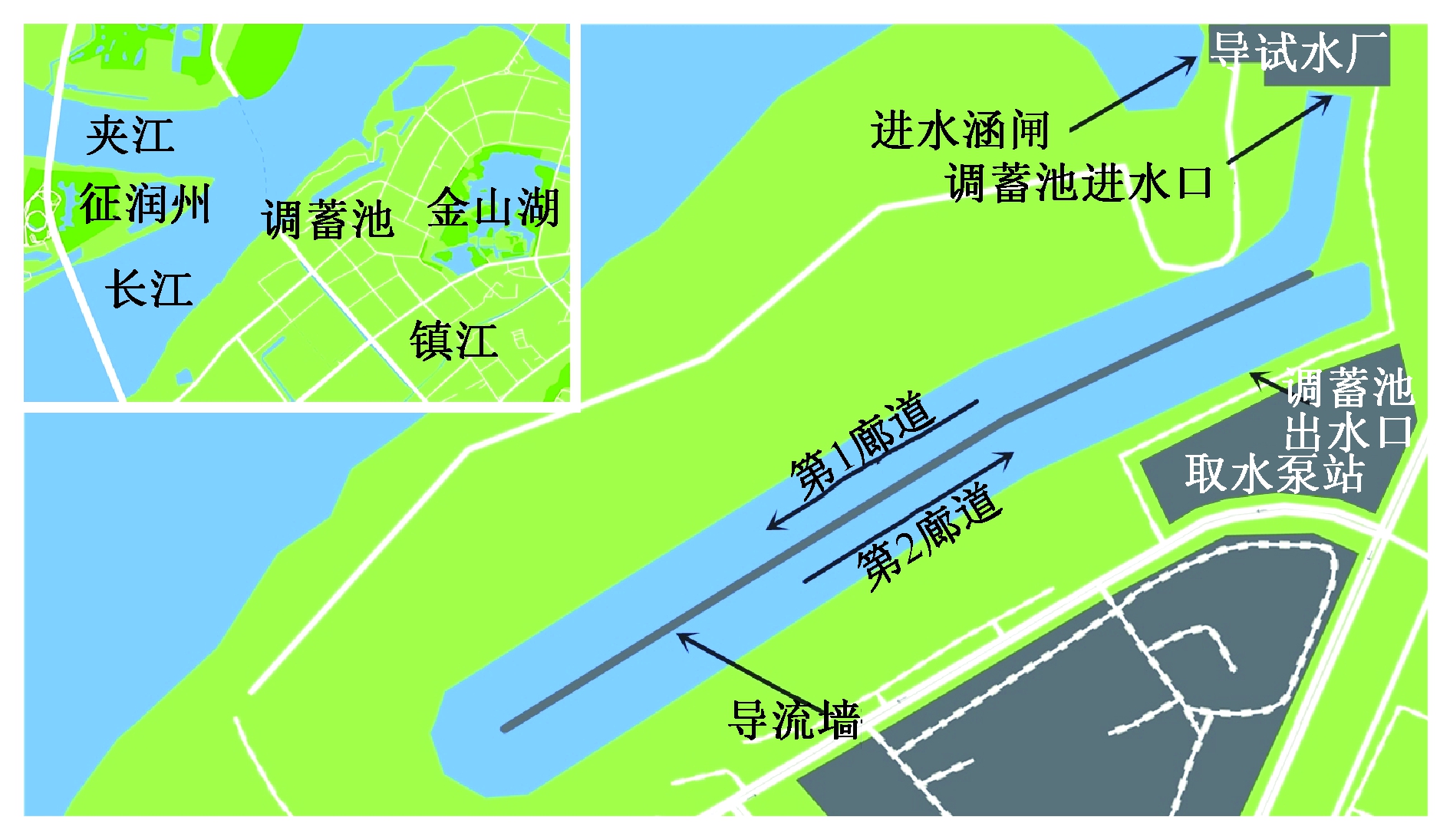
图1 调蓄池地理位置及环境背景信息示意
Fig.1 The location and background information of the storage basin
2 模型构建
2.1 EFDC简介
EFDC全称为环境流体动力学模型,是由John Hamrick根据多个数学模型集成开发研制的综合环境流体动力学软件[4]。EFDC可以模拟河流、湖泊、河口、水库、湿地、近海海域等地表水系统中的一维、二维或三维的流场、物质传输(温度、盐度、泥沙等)及生化过程(TN、TP、藻类等)的模型[4-6]。
与其他水质模型相比,EFDC模型的优势有:边界处理技术较灵活,文件输入格式通用;整合了水动力、泥沙与水质模块,无需再次耦合,操作便捷;同时整合完整的前、后处理软件,采用可视化操作界面能直接快速生成时间、空间网格数据,处理图像文件。
经过约20年的发展和完善,该模型在我国已被成功应用于云南滇池、北京密云水库、重庆两江汇流、长江流域、太湖等多个水域的数值模拟研究中[4-7]。
2.2 控制方程
EFDC采用在水平方向曲线正交坐标转换和垂直方向σ坐标变换下不可压缩的Boussinnesq假定和静水压强假定,满足质量守恒、动量守恒及能量守恒等基本规律,且能较好地拟合复杂的岸线和地形。其连续性方程、动量方程如下[6-8]:
∂t(mζ)+∂x(myHu)+∂y(mxHv)+∂z(mw)=0
(1)
∂t(mHu)+∂x(myHuu)+∂y(mxHuu)+∂z(mwu)-
(mf+v∂xmy-u∂ymx)Hv=-myH∂x(gζ+p)-
my(∂xh-z∂xH)∂zp+∂z(mH-1Av∂zu)+Qu
(2)
∂t(mHv)+∂x(myHuv)+∂y(mxHvv)+∂z(mwv)+
(mf+v∂xmy-u∂ymx)Hu=-mxH∂y(gζ+p)-
mx(∂yh-z∂yH)∂zp+∂z(mH-1Av∂zv)+Qv
(3)
式中:u、v分别为曲线正交坐标系下x、y方向的水平速度分量,w为σ坐标下z方向上的垂向速度分量,m/s;mx、my和m为Jacobian曲线正交坐标转换系数,m=mxmy;H为总水深,h为平均水深,ζ为自由水面波动位移,H=h+ζ,m;Av为垂向紊动黏滞系数;Qu、Qv为动量方程在x、y方向上的源汇项;p为压力,Pa;f为柯氏力参量;g为重力加速度,m/s2[6-8]。
EFDC污染物扩散模型建立在水动力模型的基础上,其本质为物质输运方程:
∂tC+∂x(uC)+∂y(vC)+∂z(wC)=∂x(Dx∂xC)+
∂y(Dy∂yC)+∂z(Dz∂zC)-kpC+CsS
(4)
式中:Dx、Dy、Dz分别为污染物在x、y、z 3个方向上的扩散系数;S为污染物点源排放量;kp为衰减系数;Cs为污染物源浓度值,mg/L;C为污染物浓度值,mg/L[9]。
EFDC模型方程的具体求解方法见文献[10]。
2.3 网格划分与监测点设置
要建立调蓄池三维数值模型,首先要对调蓄池进行网格概化。利用EFDC自带网格生成工具采用正交化网格,利用EFDC自带的网格生成工具[11],生成网格单元大小5 m×5m,共3549个。为精确分析污染物浓度随时间的变化,在调蓄池内置9个监测点位,如图2所示。其中,监测点1位于调蓄池进水口,监测点8位于调蓄池出水口。
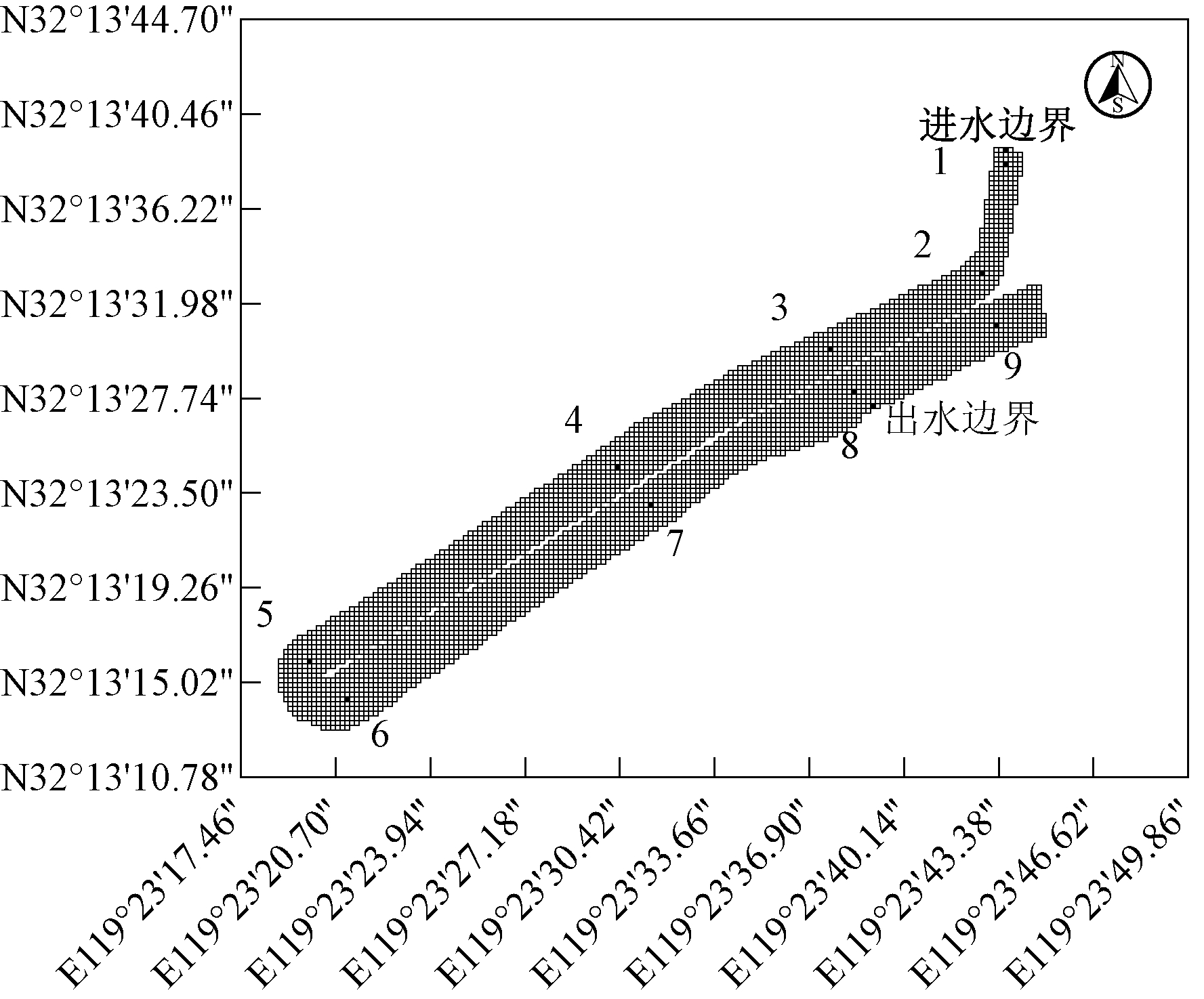
注:图中1—9为监测点位。
图2 模拟区域网格划分及监测点位
Fig.2 Regional griding and the distribution of the monitoring points
所有网格统一采用正常水位3.50 m,池底高程采用实测数据插值导入,如图3所示。因为主要考察污染物在调蓄池内水平方向的扩散且水深较浅,水流速度和水质参数垂向差异较小,所以模型垂向分层采用σ坐标分为1层,边界采用干湿单元格方案。
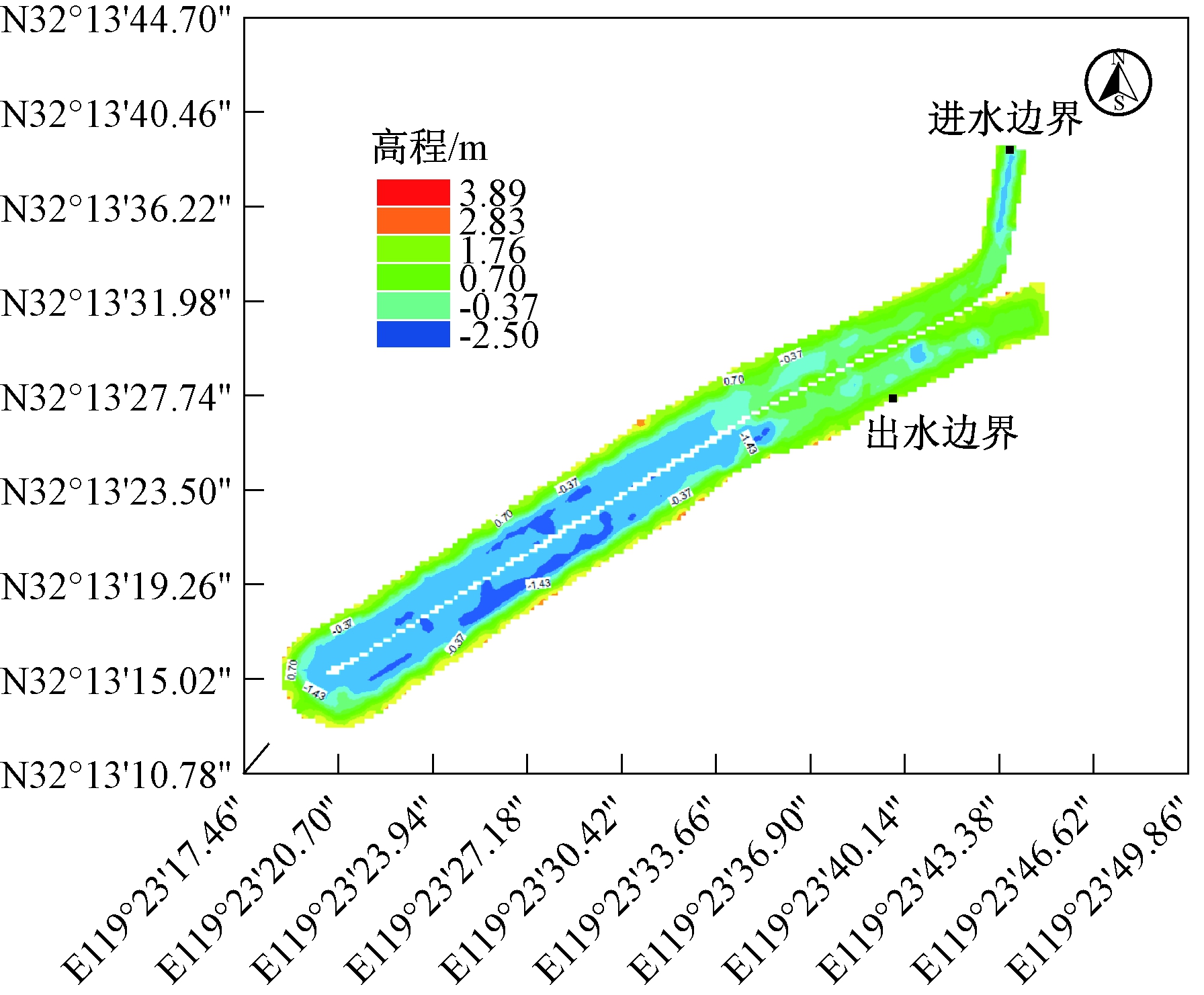
图3 调蓄池池底高程示意
Fig.3 The bottom elevation of storage basin
2.4 模拟方案与参数设置
由于缺乏前置调蓄池内突发水污染事故的历史记录,在对长江镇江段进行调查的基础上,构建污染事故场景模拟。假设污染物在长江镇江段发生污染事故泄漏,污染物除了在长江沿线扩散外,可能随水流进入调蓄池内,从而导致污染物在一段时间内以连续变化的浓度进入调蓄池。
采用Dye染色示踪模块来模拟污染物在调蓄池内的扩散,Dye模块能够模拟水中物质输运的平均年龄及滞留时间[12]。由于污染物在调蓄池内的扩散时间很短,仅以小时计,污染物的生化反应的效应很小,所以将污染物衰减系数设置为0。投加方式采用定点连续剂量投加,投加点位于调蓄池进水口,浓度变化如图4所示。

图4 进水口污染物浓度变化
Fig.4 Concentration change of pollutants in inlet
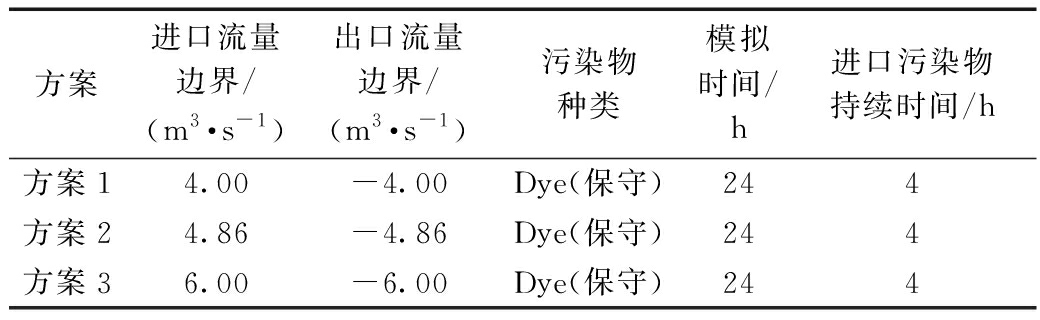
调蓄池水力停留时间约为12 h,模拟时间的设置要稍大于水力停留时间,将模拟时间设置为24 h,时间步长设置为0.3 s,每10 min输出1次结果,调蓄池粗糙系数设置为0.06。水温20 ℃,共设置3种模拟方案如表2所示。
表2 污染物扩散数值模拟方案
Table 2 Numerical simulation of pollutant diffuse scheme
方案进口流量边界/(m3·s-1)出口流量边界/(m3·s-1)污染物种类模拟时间/h进口污染物持续时间/h方案14.00-4.00Dye(保守)244方案24.86-4.86Dye(保守)244方案36.00-6.00Dye(保守)244
池内流量主要有3个具有代表性的流量:低流量、常规流量、高流量。模拟时间较短,调蓄池进出口流量变化极小,3个工况的流量边界均采用恒定流量,即模拟时间内进水或出水边界的流量保持恒定,水温为20 ℃。
2.5 模型验证
对调蓄池流场进行计算,结果如图5所示。可知:模拟水流方向与实际水流方向基本一致,调蓄池主体的断面流场基本接近于均匀流,为0.03~0.05 m/s,水动力模型的计算结果较符合实际。
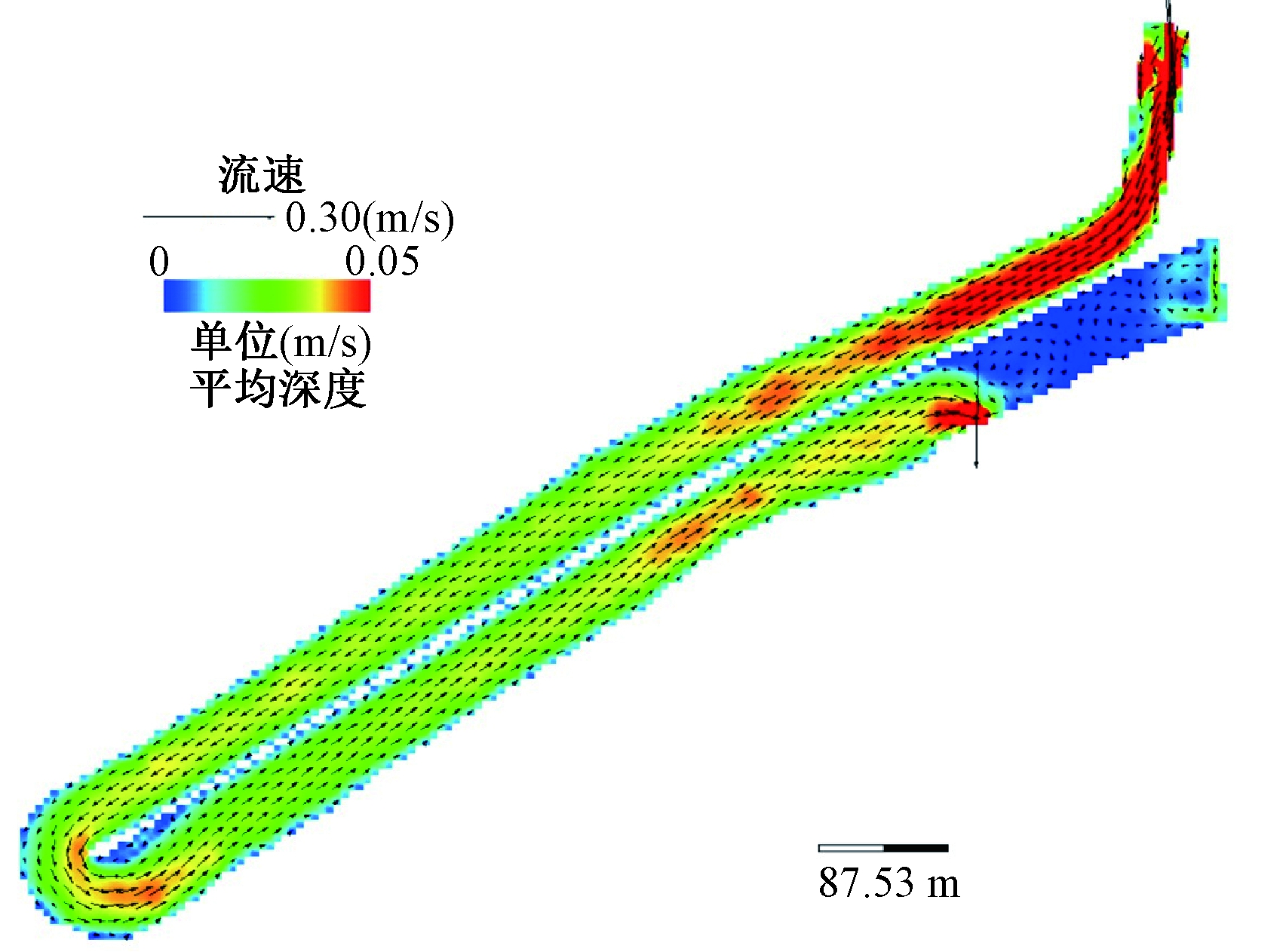
图5 调蓄池流场计算结果示意
Fig.5 The calculation results of the storage basin
选取监测点位实测断面平均流速与模拟计算结果进行对比验证。模型实测资料采用在2016年6月30日的断面流场实地检测数据,采用ADCP声学多普勒流速剖面仪测量,比较9个监测点位所在断面的模拟平均流速与实测平均流速,如图6所示。

![]() —实测断面流速;
—实测断面流速; ![]() —计算断面流速。
—计算断面流速。
图6 调蓄池断面流速验证
Fig.6 Cross-section velocity verification of storage basin
图6说明计算流速与实测流速的变化趋势基本一致,各个监测点位的断面平均流速与实测流速非常接近,平均误差仅为0.017 m/s,最大误差仅为0.041 m/s。但计算流速略大于实测流速,主要因为实测流速受到风向、底部摩擦与垂向紊流作用等影响。
验证结果表明,水动力模型能较为准确地反映调蓄池实际水动力学情况,其模拟结果可作为后续污染物模拟的基础。
3 数值模拟结果与讨论
3.1 监测点位污染物浓度变化对比分析
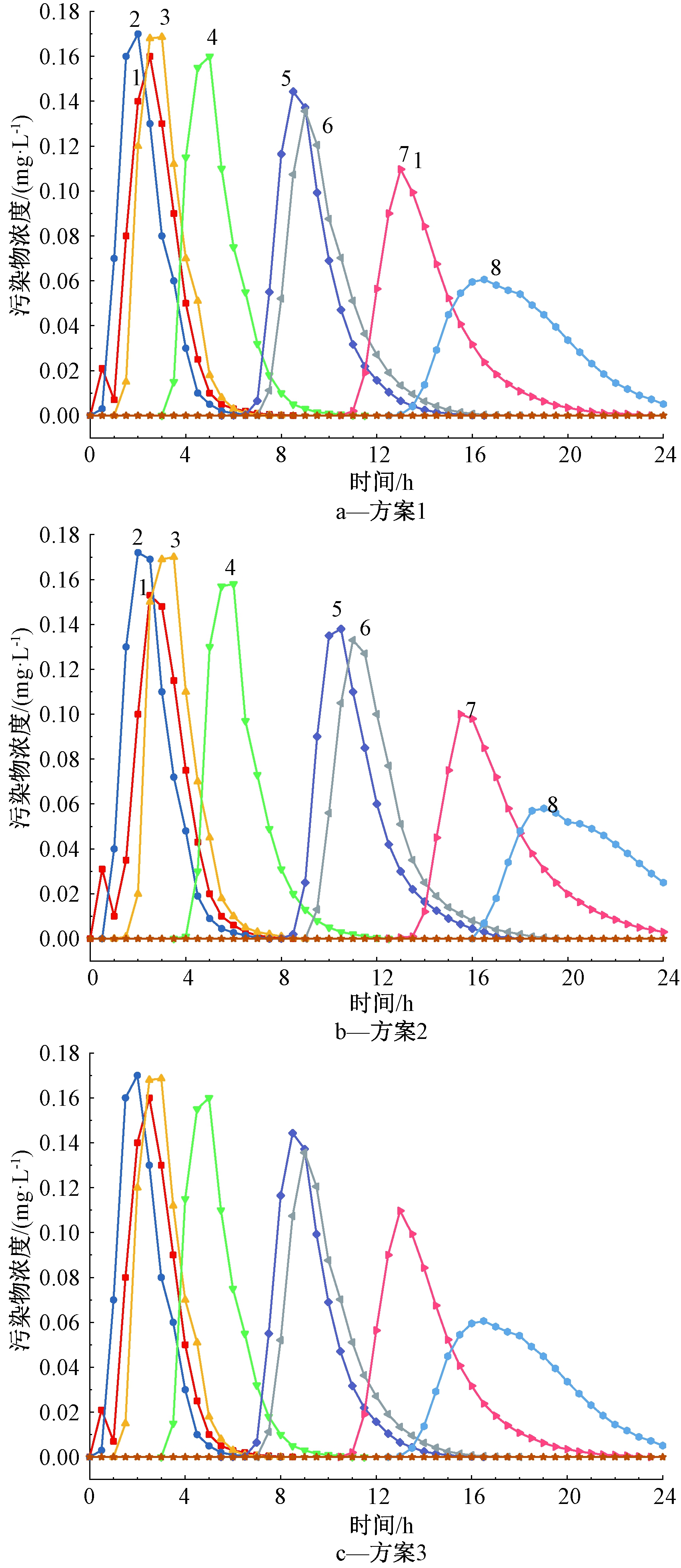
图7表示调蓄池流量在4,4.86,6 m3/s 3个工况下发生污染物泄漏事故后,污染物沿前置调蓄池流程流经第1~9个监测点位时污染物浓度变化规律。
![]() —监测点1;
—监测点1; ![]() —监测点2;
—监测点2; ![]() —监测点3;
—监测点3; ![]() —监测点4;
—监测点4; ![]() —监测点5;
—监测点5; ![]() —监测点6;
—监测点6; ![]() —监测点7;
—监测点7; ![]() —监测点8;
—监测点8; ![]() —监测点9。
—监测点9。
图7 方案1—3监测点位浓度变化
Fig.7 The concentration change of monitoring points in case Ⅰ—Ⅲ
由图7可看出:在污染物扩散过程中,污染物浓度沿程均逐渐衰减,衰减速度先慢后快,这表明水流对污染物有扩散、稀释作用;监测点污染物的过流时间沿程逐渐增大,这表明调蓄池内水体流速逐渐减小,且污染云团面积逐渐增大;3种方案监测点受污染的顺序相同,均为沿调蓄池水流方向由监测点1至监测点8依次受到污染,而监测点9位于调蓄池出水口后部的死流区不受污染,这说明流量大小不能改变污染物在调蓄池内的扩散状态。
流量越大的方案,同一监测点污染物峰值浓度相同,但污染物过流时间越短,以靠近调蓄池出水口的监测点8为例,3种方案的污染物峰值浓度均在0.09~0.11 mg/L内,但污染起始时间依次为15.8,13.0,10.6 h,这说明流量越大,污染物扩散越快,调蓄池出水口越快受到污染。
3.2 污染物扩散状态对比分析
对3种方案进行模拟计算后发现,虽然流量工况不同,但污染物的扩散分布趋势基本相同,故以方案2为例进行分析。图8为方案二的3,6,9,12,15,18 h污染物分布情况。
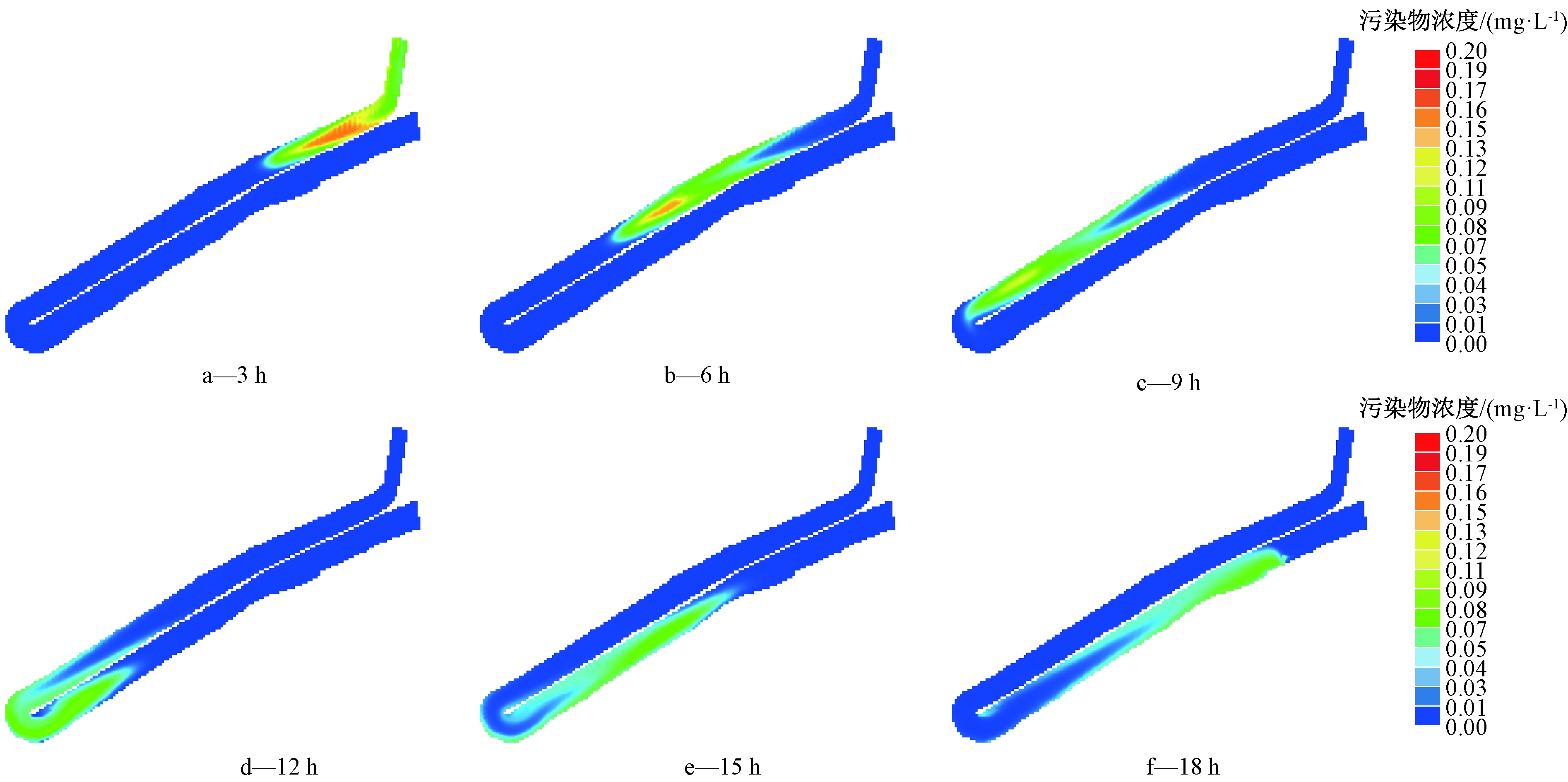
图8 方案2在不同时段污染物扩散
Fig.8 Pollutants diffusion of 3 h, 6 h, 9 h, 12 h, 15 h, 18 h in case Ⅱ
由图8可知:随着时间的推移,污染物沿调蓄池水流方向扩散,以进水口、前端、60°拐弯、第1廊道、180°拐弯、第2廊道的顺序依次扩散,最后由调蓄池出水口随水流出,这说明污染物的扩散受调蓄池形状与流场影响。
污染物在调蓄池内形成一锥形的污染云团,区域中心浓度最高,向外浓度梯度降低。随时间推移面积逐渐增大,但整体浓度逐渐降低。以方案2为例,如图9所示,2 h污染云团的峰值浓度约为0.2 mg/L,覆盖调蓄池前端及60°拐弯处,面积约为500 m2;9 h污染云团的峰值浓度下降至约0.12 mg/L,覆盖调蓄池第1廊道后段,面积约为900 m2;18 h污染云团的峰值浓度下降至约0.1 mg/L,几乎覆盖调蓄池第2廊道,面积约为1200 m2。

图9 方案2在2 h、9h、18 h污染物扩散状态示意
Fig.9 Pollutants diffusion of 2 h, 9 h, 18 h in case Ⅱ
3种方案污染物扩散速度不同,流量越大的方案扩散速度越快;流量越小的方案扩散速度越慢。以污染物云团中心扩散至调蓄池出水口为例(如图10所示):3种方案污染物云团的形状与面积基本相同,但所用时间不同,方案1用时约20 h,方案2用时约17 h,方案3用时仅约14 h。这说明流量工况不同,污染物的扩散存在速度梯度差。
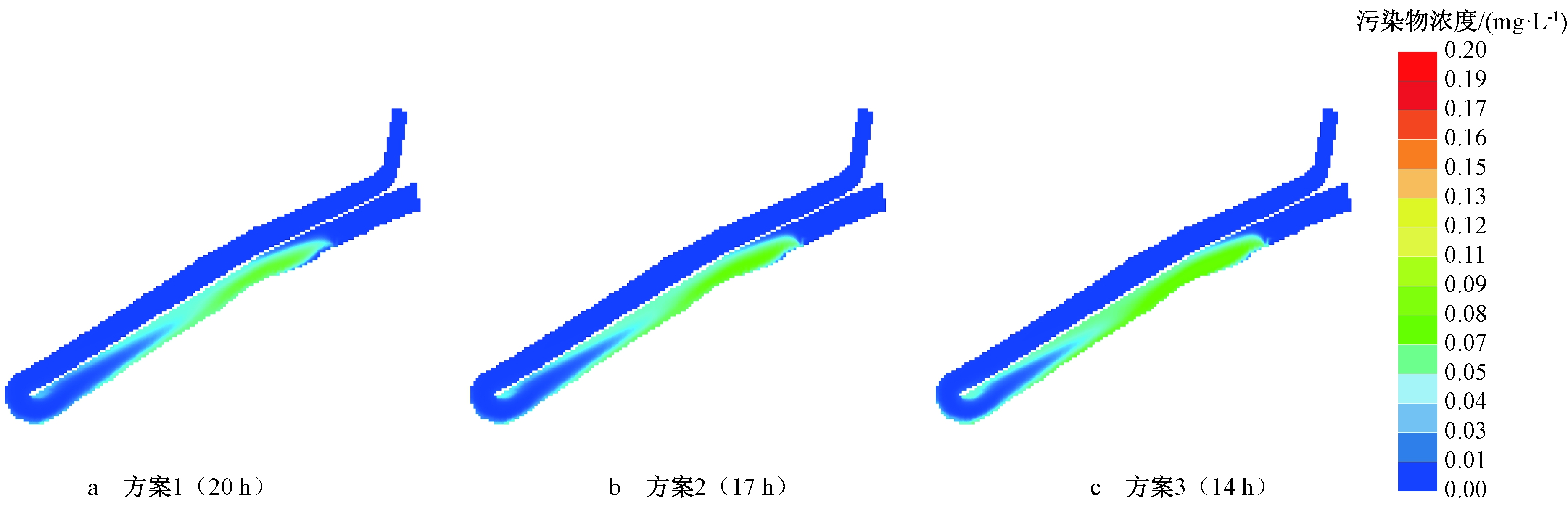
图10 3种方案在污染物扩散至调蓄池出水口拐弯状态示意
Fig.10 Pollutants diffusion of storage basin outlet in three cases
3.3 污染物扩散距离与扩散速度对比分析
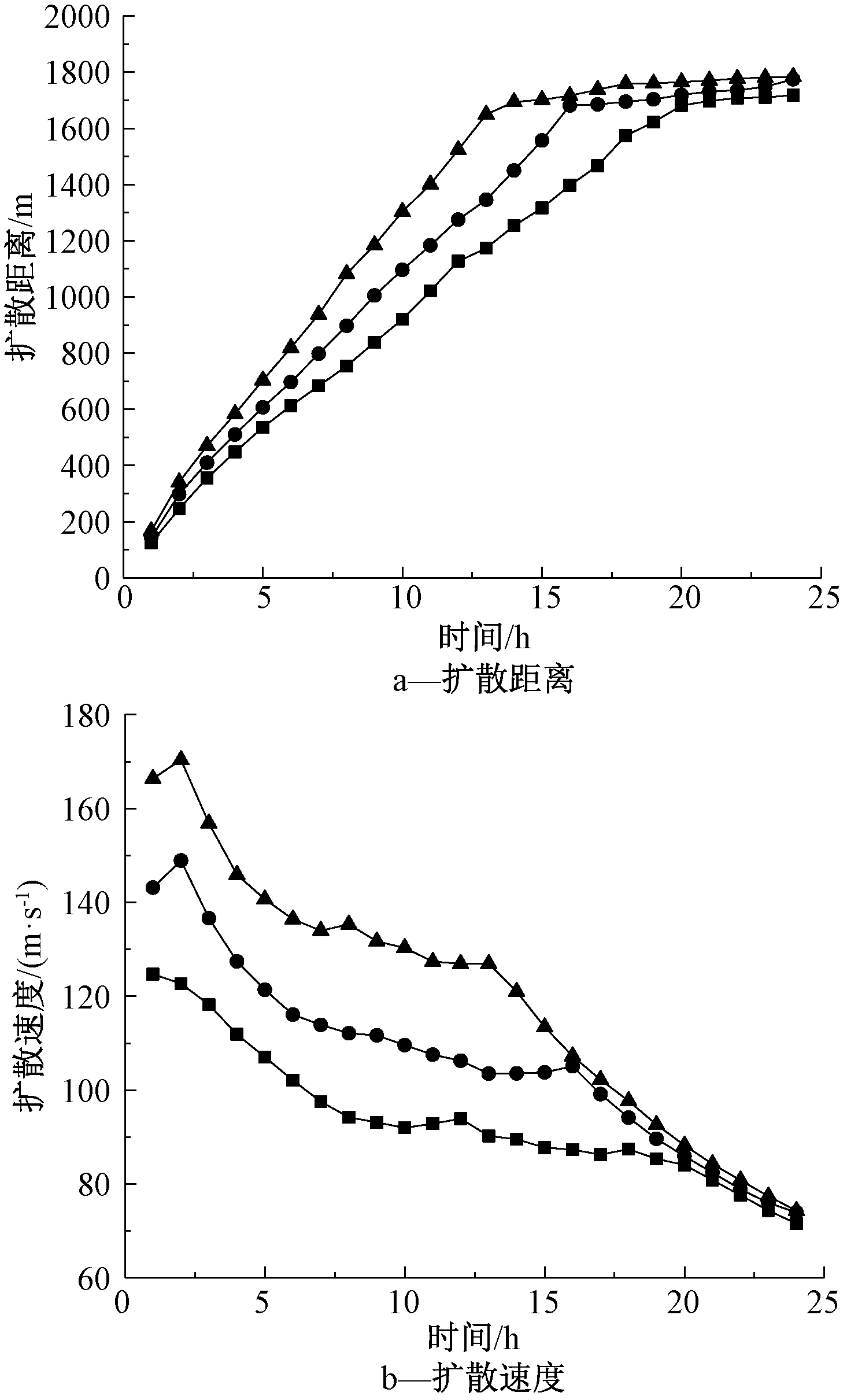
3种方案污染物扩散距离与扩散速度如图11所示。
![]() —方案1;
—方案1; ![]() —方案2;
—方案2; ![]() —方案3。
—方案3。
图11 3种方案污染物扩散距离和扩散速度
Fig.11 Pollutants diffusion distance of three cases
由图11可知:3种方案扩散距离与扩散速度的变化趋势基本相同。扩散距离均逐渐增大,这表明污染云团先稳定扩散,在到达约1800 m后基本停止。流量越大的方案污染物越早到达1800 m,这表明大流量时发生污染事件调蓄池出水口污染时间越短。
3种方案的扩散速度均逐渐减小,污染云团刚进入调蓄池,由于进水口流速较快且污染云团浓度较高,扩散速度很快,之后均匀稳定地减小。这说明污染物的初始扩散速度由流量决定,流量越大扩散速度越快。
3.4 调蓄池预警应急响应
位于调蓄池进水口处导试水厂中的水质监测站24 h运行,能实时监控进入调蓄池水体的污染情况。若调蓄池在最不利工况下发生突发水污染事件,根据数值模拟结果,污染物最快到达调蓄池出水口的时间为10 h,水质监测站的污染物响应时间为6 h,此时污染物仅扩散至第1廊道后段,还未进入第2廊道,管理人员有充足的时间对突发水污染事件进行应急处理。
当水质监测站检测到污染物进入调蓄池后,位于调蓄池进水口的双向泵房反向排水,同时位于调蓄池前端的应急处理设施(药剂投加、曝气等)开始运行[3],金山湖备用水源由调蓄池尾端进入,在供水的同时进入调蓄池内促进反向排空污染水,在污染事件发生后既保证了镇江水厂的供水安全持续,又促进了污染物的排出。
4 结 论
1)污染物在调蓄池内迁移扩散路径主要是按照池内流场方向进行的,同时存在横向扩散。污染云团以锥形较快地稀释与扩散,中心浓度最高,向外梯度降低;污染物浓度随时间逐渐降低、分布逐渐均匀;扩散距离逐渐增大、扩散速度逐渐减小。
2)流量大小不能改变污染物的扩散趋势,也不能改变污染云团的变化规律,污染物的扩散趋势与云团变化主要受到调蓄池形状与流场的影响;但流量大小是影响污染物扩散速度的因素,流量越大污染物扩散速度越快,污染物扩散至调蓄池出水口用时越短。
3)调蓄池在3种流量工况下,污染物扩散至出水口用时分别为15.8,13.0,10.6 h,工作人员有足够的时间进行预警响应并处理,调蓄池对污染物的调蓄作用得以有效发挥。
4)数值模拟能对突发水污染事件后调蓄池内污染物迁移进行快速的模拟与预测,并能在地理与时间尺度上以二维动画形式实时展示污染物迁移的状态与规律,可为镇江自来水公司水源预警提供决策依据。
[1] 蒋海涛,容明知.建立长江下游饮用水源安全保障体系的若干思考[J].人民长江, 2011, 42(2):39-41.
[2] 张昊,张代钧.复杂水环境模拟研究与发展趋势[J].环境科学与管理, 2010, 35(4):24-28.
[3] 张晓健,陈超,谢继步,等.自来水厂原水的调蓄与水质控制[J].中国给水排水, 2016, 32(22):14-19.
[4] 杨倩.基于EFDC的密云水库水环境及应急处理模型研究[D].北京:中国地质大学(北京), 2005.
[5] 樊乔铭,丁志斌.基于EFDC的港口污水处理厂排放标准及排污口选划研究[J].环境工程, 2016,3(3):147-152.
[6] 张文时.基于EFDC模型的山地河流水动力水质模拟:以重庆市赵家溪为例[D].重庆:重庆大学, 2014.
[7] 张洪.基于EFDC模型滇池外海水环境仿真研究[D].浙江:浙江大学, 2017.
[8] 孙凯迪.汾河水库突发水污染事件应急模拟研究[D].太原:太原理工大学, 2018.
[9] 李林子.突发性水污染事故影响的预测预警体系研究[D].南京:南京大学, 2011.
[10] Teera Technologies,INC. The environmental fluid dynamic code theory and computation[M].Washington DC: USEPA, 2007.
[11] 唐天均,杨晟,尹魁浩,等.基于EFDC模型的深圳水库富营养化模拟[J].湖泊科学, 2014, 26(3):393-400.
[12] 李杰,林晶,吴增茂.Falls Lake水库内溶解物输运模拟[J].水科学进展, 2011, 22(3):413-420.