0 引 言
双电极静电除尘器(ESP)因其处理烟气量大、除尘效率高、投资运行经济等特点在工业粉尘治理领域得到了广泛应用[1],但其对于高比电阻粉尘的捕集效果一直不理想[2]。为了提高ESP对粉尘比电阻的适应能力,带辅助电极的三电极除尘器应运而生[3]。三电极静电除尘器在2个主电极之间添加了等位的辅助电极,其独特的电场特性使除尘器对高低比电阻粉尘都产生了良好的捕集效果。而无论在何种电极结构的ESP中,扩散荷电对细微颗粒捕集的影响都不容忽视。
目前国内对扩散荷电的研究主要集中在基础性分析方面。郑士金[4]对静电除尘原理及其效应进行了初步探讨,指出了静电除尘器中离子不仅在电场作用下运动,还在其自身的热扩散运动过程中附着在微粒上使其荷电。崔宝欣[5]分析并讨论了在电场荷电和扩散荷电复合荷电机理下粉尘粒子的荷电率。Zhang等[6]采用Fluent软件数值模拟的方法对扩散荷电作用对线板式静电除尘器中PM10颗粒捕集效率的影响进行了研究。严佩等[7]通过建立高温线板式静电除尘系统研究得出了高温环境可以促进颗粒扩散荷电。国外对扩散荷电的研究则侧重理论公式推导。Arendt等[8]阐述了扩散荷电对细微颗粒荷电影响明显,并以数学形式进行表示。 White[9]通过推导更为精确的扩散荷电方程式,确立了扩散荷电是ESP中细微颗粒主要荷电方式。Liu等[10]利用一种新的电场下气溶胶颗粒荷电理论来研究扩散荷电和电场荷电2种荷电方式下离子的运动。Long等[11]通过将不同颗粒荷电模型在ESP中的数值求解结果与试验进行对比,验证了Lawless模型是考虑扩散荷电和电场荷电作用下的最优颗粒荷电模型。
综上所述,国内外对扩散荷电的研究主要集中在其本身的荷电机制方面,即机理和理论分析上,而对扩散荷电在不同电极结构ESP中的效应表现尚未见报道。为了探明其在不同结构ESP中的贡献,本文对比分析了三电极和双电极ESP中扩散荷电效应,相关结果可为三电极ESP性能提升提供参考。
1 理论模型
1.1 多场耦合关系
三电极和双电极ESP内部存在电场、流场和颗粒动力场[12],其关联、耦合作用如图1所示。电场通过离子风影响流场,通过电场力(扩散荷电和电场荷电联合作用)影响颗粒动力场;流场通过离子对流反作用于电场,通过空气动力拖曳力作用于颗粒动力场;颗粒动力场通过空间电荷来影响电场的分布,通过气-固两相耦合影响流场。

图1 多场耦合示意
Fig.1 Schematic diagram of multi-field coupling
1.2 电 场
三电极、双电极ESP均为线板式结构,在电晕稳定放电情况下,可采用以下Poisson方程和电流连续性方程来描述电场分布:
(1)
(2)
式中:ε0为真空介电常数,![]() 为电场强度,N/C;ρ为空间电荷密度,
为电场强度,N/C;ρ为空间电荷密度,![]() 为电流密度矢量,A/m2。
为电流密度矢量,A/m2。
1.3 流 场
由于静电除尘器中的压降变化小,可将气体视为不可压缩牛顿流体,考虑将Navier-Stokes方程中的广义源项用空气动力学拖曳力和电体积力之和来替代,气体流场的质量守恒和动量守恒方程可分别表示为[13]:
(3)
(4)
式中:ρg为烟气密度,kg/m3;ui、uj分别为气体在平行于收尘极方向速度分量和垂直于收尘极方向速度分量,m/s;P为气体平均静压,Pa;μ为气体动力黏性系数,kg/(m·s);μt为湍流动力黏性系数,kg/(m·s);FDj为拖曳力,N;Ej为电场强度,N/C。
1.4 颗粒动力场
除电场力、黏性阻力和离子风力外,颗粒的其他受力如重力、压差力、Basset力等均可以忽略不计[12],故颗粒的作用力平衡方程可以表示为:
(5)
式中:mp为颗粒质量,kg;Fe为电场力,Fe=QpEj,N。其中,Qp为尘粒荷电量,包括电场荷电量和扩散荷电量,C;Fi为离子风力,![]() 其中vi为离子风速,m/s,Di为尘粒直径,m。
其中vi为离子风速,m/s,Di为尘粒直径,m。
2 扩散荷电机理
扩散荷电量Qdiff计算式为[12]:
(6)
式中:K0为玻耳兹曼常数,1.38×10-23 J/K;T为ESP内温度,取450 K;qe为电子荷电量,1.6×10-19 C;N0为单位体积内平均离子数密度,个/m3;t为颗粒在电场中运动的时间,s;mion为离子质量,kg。
分析式(6)不难发现,在不考虑常数的条件下,扩散荷电量受电场内离子数密度N0和粒子在颗粒场中滞留时间t的影响。由于同一工作电压下离子浓度变化不大[15],扩散荷电量在2种ESP中受离子浓度的影响可以忽略。相比双电极ESP,三电极ESP增加了辅助电极,场强和电场力随之增大,促进了粒子朝收尘板的运动,减少了粒子在颗粒场中的停留时间,进而削弱了扩散荷电效应。
3 数值计算参数设置
3.1 结构参数
2种线板式ESP模型大小均参考已得到广泛认可的静电除尘器尺寸,具体参数见表1[16]。三电极ESP结构简化模型见图2,将辅助电极去除时即为双电极ESP的结构模型。
表1 三电极ESP结构参数设定
Table 1 Structure parameter setting of three-electrode ESP m
主电极半径r1线板距S1主电极间距S2主辅电极间距S30.0010160.11430.0760.01905
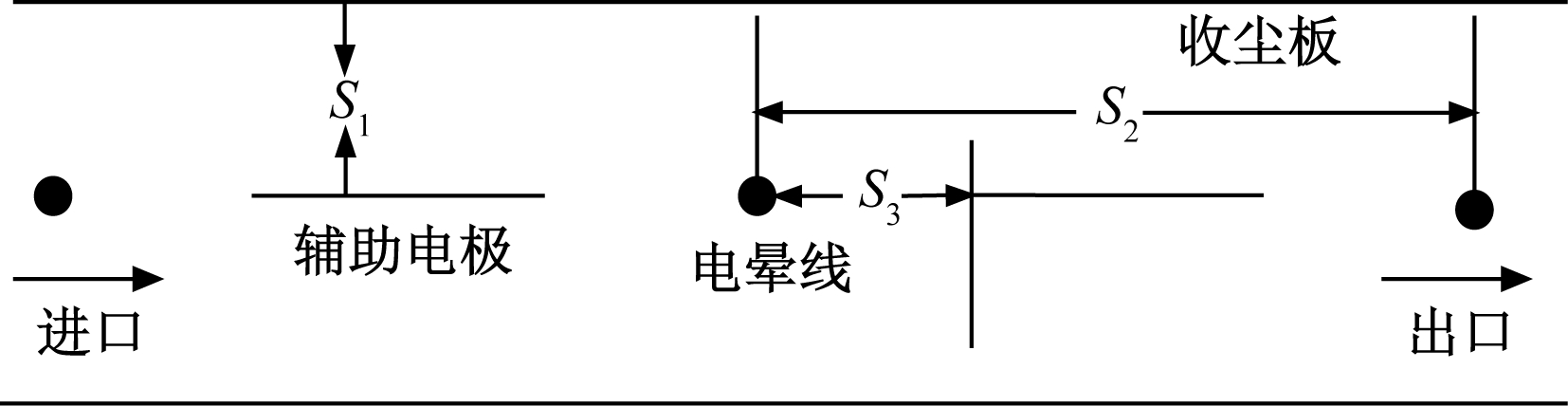
图2 三电极ESP结构简化模型
Fig.2 Simplified structure model of three-electrode ESP
3.2 气固相参数和边界条件
在对静电除尘器进行数值模拟过程中,为了客观反映实际工况,需要根据实际情况对颗粒相和气相物性参数进行设定。
由于本文研究的细微颗粒主要是燃煤电厂排放物,根据燃煤电厂的实测数据,粉尘物性参数设置如表2所示,粉尘的物质属性为无烟煤,粉尘粒径范围为1~10 μm,粒径满足Rosin-Rammler,其分布指数为1.64,中位粒径为5 μm。
表2 入射颗粒的物性参数的设定
Table 2 Physical parameter setting of incident particles

密度/(kg·m3)定压比热/(J·kg-1·K-1)导热系数/(W·m-1·K-1)210016800.0454
在FLUENT设置求解过程中,两相流采用离散相模型,其中气相物质被看作连续介质。由于烟气与粉尘只在物理意义上发生动量和能量交换,不涉及化学反应,故可将烟气简化为空气,烟气压力为大气压,即P=1.01×105 Pa。进口烟气在ESP入口处均匀分布且流速方向与之垂直,忽略电晕线对烟气流动的影响,根据大气压力下标准烟气的热物理性质表[17]线性插值得到TESP=450 K下烟气的密度、定压比热及热导率。
线板式ESP的具体边界条件设置如表3所示。烟气入口边界采用速度入口边界条件,烟气流动出口边界条件设为压力出口条件。电晕线表面的电势给定为V0,三电极ESP辅助电极表面电势给定为V0,双电极ESP辅助电极表面电势条件设置为 V=0,收尘极板表面的电势为0。计算时在收尘极板和电晕线表面采取标准壁面函数法,利用一组半经验的公式(壁面函数)将壁面上的物理量与湍流核心区内的相应物理量联系起来。
V=0,收尘极板表面的电势为0。计算时在收尘极板和电晕线表面采取标准壁面函数法,利用一组半经验的公式(壁面函数)将壁面上的物理量与湍流核心区内的相应物理量联系起来。
表3 线板式ESP边界条件
Table 3 Boundary conditions
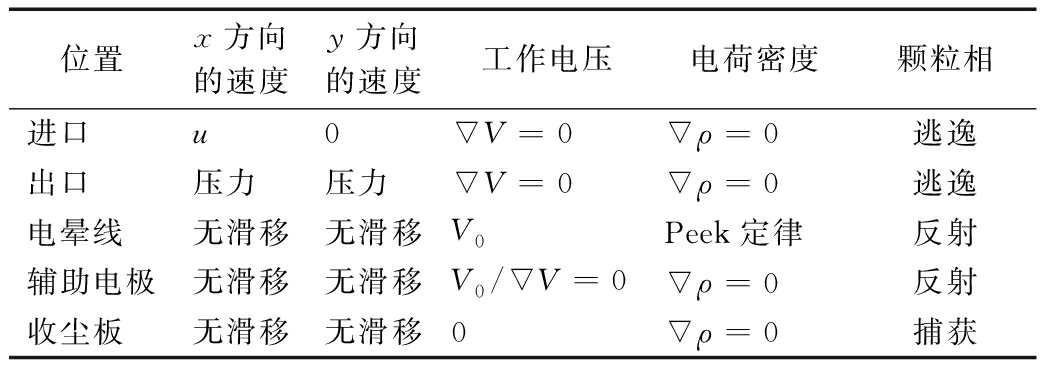
位置x方向的速度y方向的速度工作电压电荷密度颗粒相进口u0∇V=0∇ρ=0逃逸出口压力压力∇V=0∇ρ=0逃逸电晕线无滑移无滑移V0Peek定律反射辅助电极无滑移无滑移V0/∇V=0∇ρ=0反射收尘板无滑移无滑移0∇ρ=0捕获
4 结果与讨论
4.1 颗粒运动轨迹的对比
为了直观地看出2种ESP中扩散荷电对除尘性能的影响,设工作电压均为30 kV,烟气流速为1 m/s, 颗粒粒径采用R-R分布。2种ESP中的颗粒运动轨迹分别如图3和图4所示,对比分析后可知:考虑扩散荷电效应时,2种ESP中的颗粒运动轨迹会更加偏向收尘极板,且这种偏向趋势在双电极ESP中更明显。
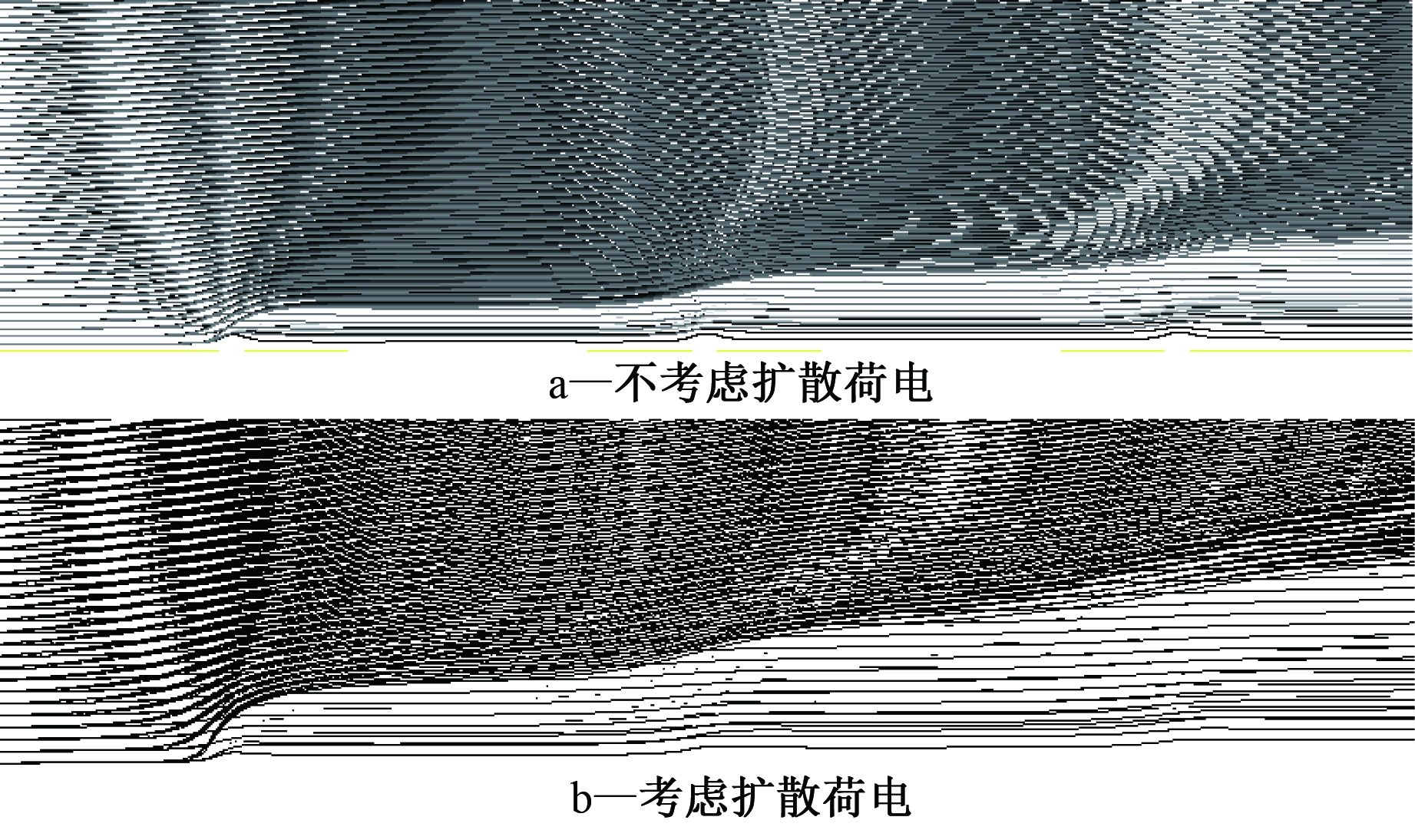
图3 双电极ESP中的颗粒运动轨迹
Fig.3 Particle trajectories in double-electrode ESP
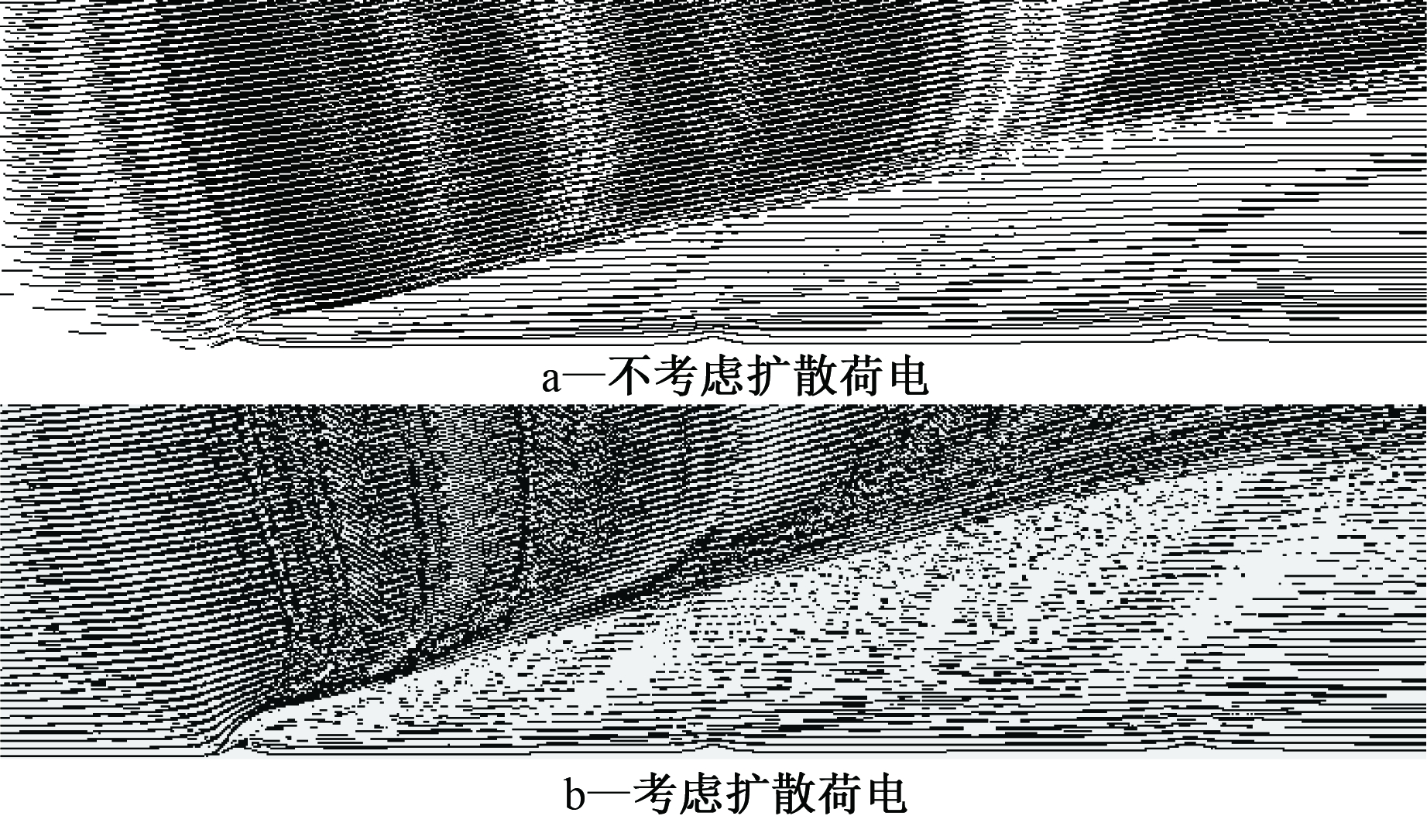
图4 三电极ESP中的颗粒运动轨迹
Fig.4 Particle trajectories in the three-electrode ESP
4.2 扩散荷电对分级除尘效率影响的对比
为了探究扩散荷电对三电极和双电极ESP中颗粒除尘效率的影响,图5是在与图4相同工况下的颗粒分级除尘效率。由图5可知:随着颗粒粒径增大,ESP的分级除尘效率不断上升并趋于平缓,且扩散荷电对分级效率的影响逐渐减弱;双电极ESP的曲线间距宽于三电极ESP,说明扩散荷电效应在双电极ESP中更明显,这与本文分析扩散荷电机理所得到的结论一致;与三电极ESP相比,扩散荷电对双电极ESP分级效率影响的粒径区域更大。

![]() —三电极考虑扩散荷电;
—三电极考虑扩散荷电; ![]() —双电极考虑扩散荷电;
—双电极考虑扩散荷电; ![]() —三电极不考虑扩散荷电;
—三电极不考虑扩散荷电; ![]() —双电极不考虑扩散荷电。
—双电极不考虑扩散荷电。
图5 2种ESP中扩散荷电对颗粒分级除尘效率的影响
Fig.5 Effect of diffusion charging on grade efficiency in two ESPs
为了清晰地显示2种ESP中扩散荷电效应的差异,结合图5给出了2种ESP中扩散荷电对分级除尘效率贡献率的变化曲线(图6)。可知:扩散荷电对分级除尘效率的贡献率随粒径增大呈非线性下降并逐渐趋于0;相比于三电极ESP,双电极ESP在细微颗粒粒径范围内下降幅度更大。
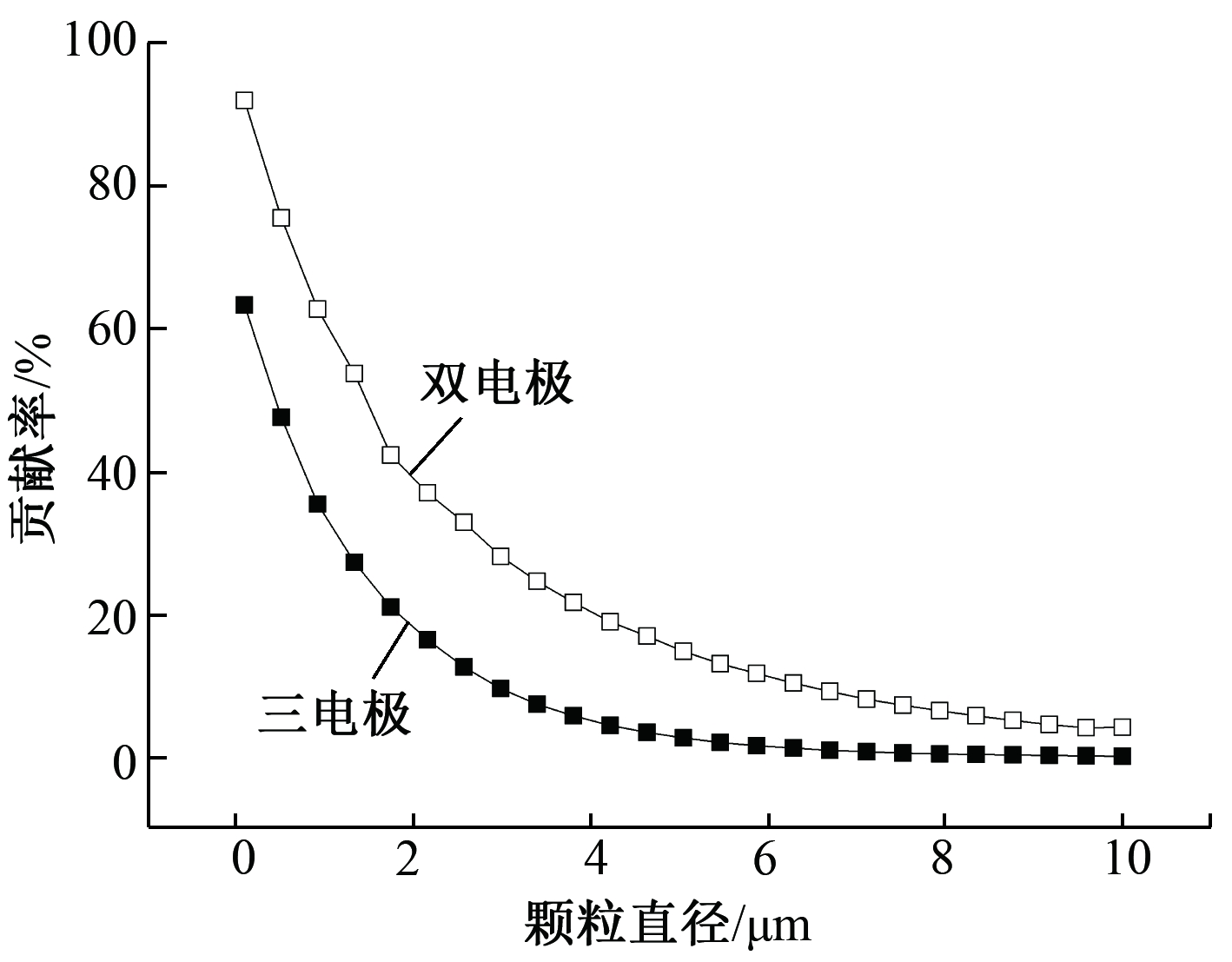
图6 2种ESP中扩散荷电对颗粒分级除尘效率的贡献率
Fig.6 Contribution rates of diffusion charging to grade efficiency in two ESPs
4.3 扩散荷电对综合除尘效率影响的对比
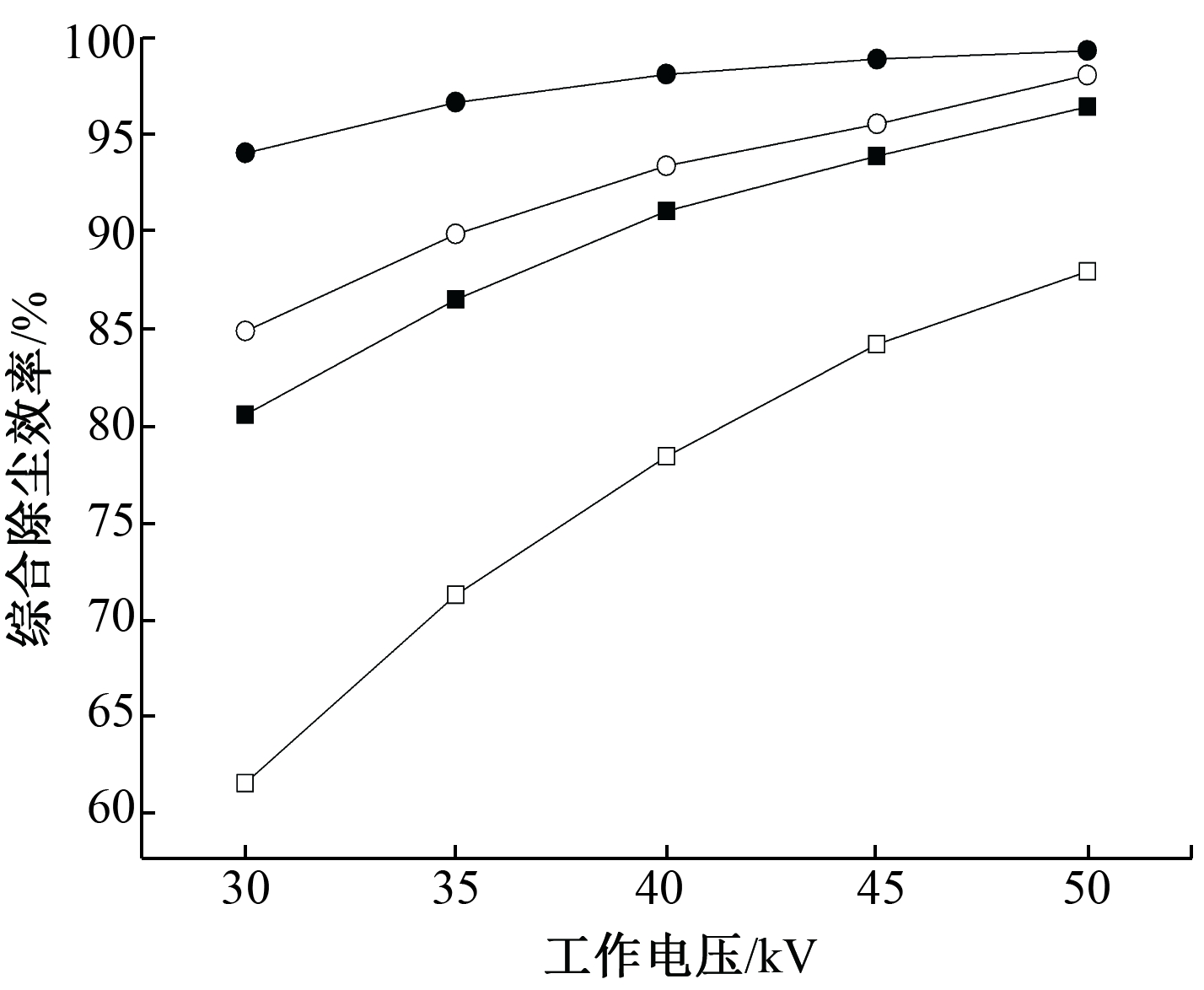
图7为不同工作电压下2种ESP中是否考虑扩散荷电效应的综合除尘效率。可知:随着工作电压降低,ESP的综合除尘效率不断减小,扩散荷电效应随之而增强;三电极ESP曲线间距相对较小,进一步证明了扩散荷电效应对双电极ESP影响更大。
![]() —三电极考虑扩散荷电;
—三电极考虑扩散荷电; ![]() —双电极考虑扩散荷电;
—双电极考虑扩散荷电; ![]() —三电极不考虑扩散荷电;
—三电极不考虑扩散荷电; ![]() —双电极不考虑扩散荷电。
—双电极不考虑扩散荷电。
图7 2种ESP中扩散荷电对颗粒综合除尘效率的影响
Fig.7 Effect of diffusion charging on overall efficiency in two ESPs
为了说明不同电极结构中的扩散荷电效应,结合图7可得到扩散荷电对综合除尘效率的贡献率,如图8所示。可知:贡献率均随工作电压的增大而减小,对于双电极ESP而言,该减幅更大;三电极ESP的曲线位于下方,贡献率明显低于双电极,同样说明双电极ESP中扩散荷电效应更强。
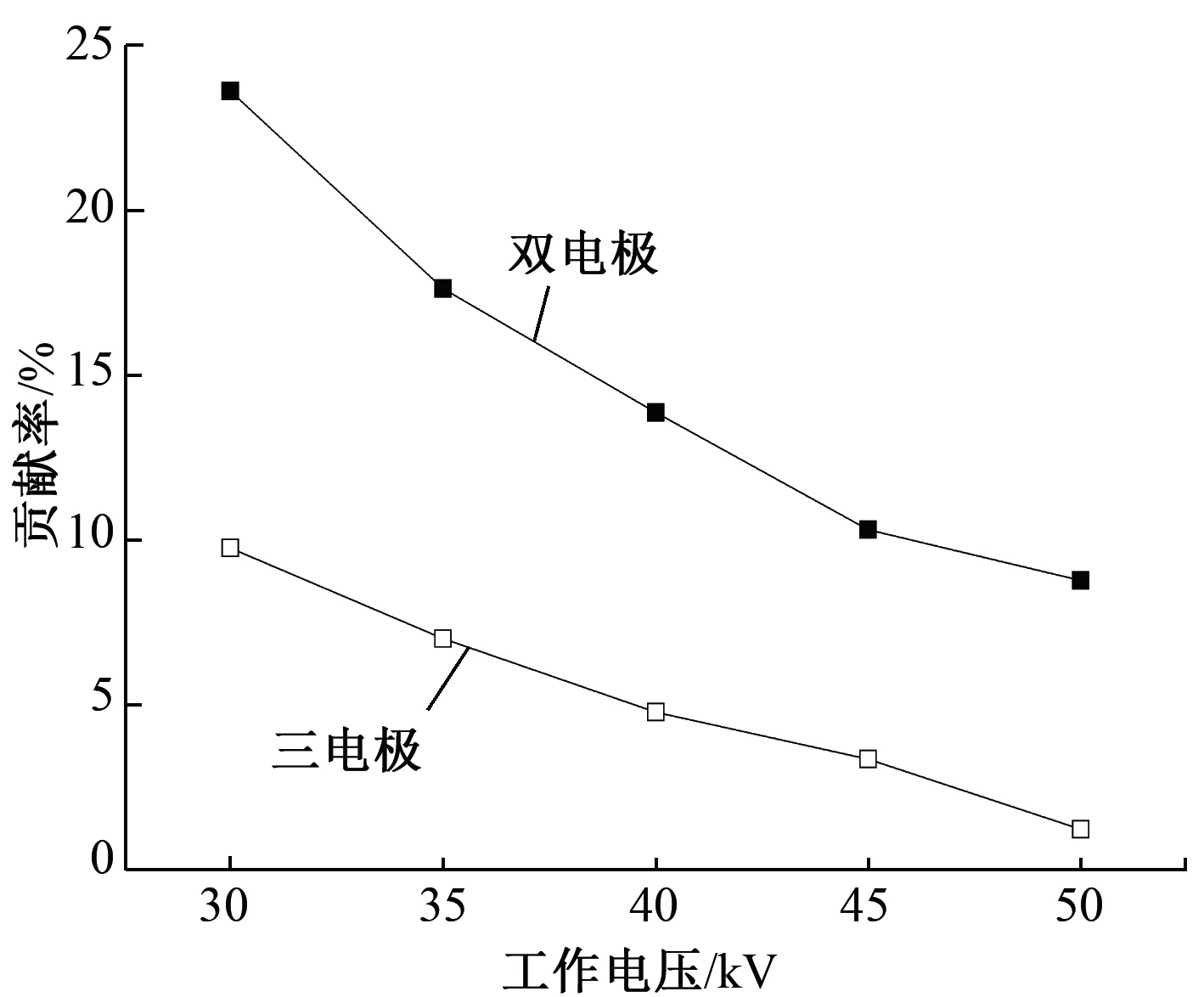
图8 2种ESP中扩散荷电对颗粒综合除尘效率的贡献率
Fig.8 Contribution rate of diffusion charging to overall efficiency
in two ESPs
5 结 论
在建立ESP内部多场耦合理论模型的基础上,通过机理分析和Fluent模拟对比了2种电极结构ESP中的扩散荷电效应,得到如下结论:
1)相比于三电极ESP,双电极ESP中扩散荷电效应更显著。
2)随着颗粒粒径的减小,扩散荷电对分级除尘效率的贡献率呈强非线性增大趋势,且在双电极ESP中的趋势更明显。
3)随着工作电压的降低,扩散荷电对综合除尘效率的贡献率不断增大,且在双电极ESP中影响更大。
[1] 蔡伟龙, 胡恭任, 罗祥波. 我国燃煤电厂除尘技术路线选择问题分析 [J]. 环境工程, 2015, 3(5): 100-103.
[2] 陈玲, 夏良健, 高鹏. 双极荷电静电除尘器收集高比电阻微尘的实验 [J]. 环境工程, 2007, 25(4): 34-37.
[3] 亢燕铭, 党小庆, 张晓玲. 三电极电除尘器的电流特性 [J]. 中原工学院学报, 2003, 14(增刊1): 46-48.
[4] 郑士金. 电除尘原理及其效应的初探 [J]. 有色矿冶, 1993(6): 30-34.
[5] 崔宝欣. 复合电晕场中粉尘粒子的荷电机制 [J]. 烟台师范学院学报(自然科学版), 1998, 14(2): 106-109.
[6] Zhang J P, Du Y Y, Wu H, et al. A numerical simulation of diffusion charging effect on collection efficiency in wire-plate electrostatic precipitators [J]. IEEE Transactions on Plasma Science, 2011, 39(9): 1823-1828.
[7] 严佩, 翁卫国, 郑成航, 等. 水泥窑尾粉尘性质对高温静电捕集的影响规律 [J]. 浙江大学学报(工学版), 2017, 51(10): 1959-1966.
[8] Arendt P, Kallmann H. The mechanism of charging mist particles [J]. Zeitschrift Fur Physikalische Chemie-International Journal of Research in Physical Chemistry & Chemical Physics, 1926, 35: 421-441.
[9] White H J. Industrial electrostatic precipitation [M]. Addison Wesley, Reading Mass, 1963.
[10] Liu B Y H, Yeh H C. On the theory of charging of aerosol particles in an electric field [J]. Journal of Applied Physics, 1968, 39(3): 1396-1402.
[11] Long Z W, Yao Q. Evaluation of various particle charging models for simulating particle dynamics in electrostatic precipitators [J]. Journal of Aerosol Science, 2010, 41(7): 702-718.
[12] Zhang J P, Zhang X, Shi F F, et al. Diffusion charging effects on PM10 collection efficiency in a wire-pipe ESP under multi-field coupling [J]. Environmental Engineering and Management Journal, 2016, 15(11): 2367-2374.
[13] Moayedi H, Amanifard N, Deylami H M, et al. Numerical investigation of using micropolar fluid model for EHD flow through a smooth channel [J]. Journal of Electrostatics, 2017, 87: 51-63.
[14] 李庆. 基于激光测量技术的煤尘污染静电治理研究 [D]. 保定:河北大学, 2008.
[15] 王凤鸣. 静电除尘器荷电粒子在电场中运动方式研究 [D]. 保定:河北大学, 2006.
[16] Penney G W, Matick R E. Potentials in D-C corona fields [J]. American Institute of Electrical Engineers, Part I: Communication and Electronics, 1960, 79(5): 91-99.
[17] Xiang X D. Modern Aerosol Particle Collection Theory and Technology [M]. Beijing: Metallurgical Industry Press, 2002.