0 引 言
地下水系统的隐蔽性、复杂性以及地下水水体自净能力差等特点决定了地下水污染治理工作难度大、耗资高、耗时长[1]。因此,在地下水资源的保护措施上必须实现从“先污染,后治理”向“预防为主,防治结合”的转变[2]。建立地下水污染预警模型,在地下水环境恶化之前及时给出可靠的警报信息,可为地下水资源管理部门提供有力的技术支撑。
国外对于水污染预警的研究始于20世纪70年代,预警的关键技术是利用传感器和生物对水质动态进行实时监测[3]。随后,国外开始根据地下水脆弱性与污染风险评价结果对重要水源地进行实时监测预警[4-5]。我国对地下水污染预警的研究始于21世纪初,其中,洪梅等[6]提出了地下水水质预警系统;之后一些学者探索了基于地下水污染风险评价、灰色预测以及风险管理的地下水污染预警模型[7-9],但尚未见回归分析方法在地下水污染预警领域的研究报道。
回归分析是采用一定的数学表达式来描述1个或几个变量的变化对另一个变量的影响程度,可以准确计量各变量之间的相互关系,达到良好的预测效果[10]。回归分析在环境预警领域的研究已出现在大气污染、地表水水质等方面[11-12]。本研究以北京市平谷区平原地区地下水水体为研究对象,采用逻辑回归和逐步回归分析各水质指标变化对地下水污染的影响程度,建立地下水污染预警模型,以期为统计分析模型在环境污染预警领域的应用提供一种新的思路和方法。
1 资料数据和分析方法
1.1 资料数据
本研究将北京市平谷区平原地区作为研究区域。基于实际地质结构和地下水水力联系,对第四系地层中的含水层进行组合,在垂向上划分出4个含水层组[13]。选取北京市水文地质工程地质大队提供的2010—2017年北京市平谷区平原地区39个地下水监测点位的主要水质指标监测数据进行统计分析,包括氨氮、氯化物、硫酸盐、氟化物、硝酸盐、溶解性总固体、铁(Fe2+和Fe3+)、亚硝酸盐、耗氧量、总硬度、pH共11项水质指标。
1.2 分析方法
1.2.1 逻辑回归分析
对于地下水污染预测模型而言,所要回归的随机变量为污染发生的概率Pi,Pi的取值范围为[0,1]。而地下水是否污染并非连续变量,假设受污染时Pi=1,未受污染时Pi=0,此时因变量为分类变量,因此一般的多元线性回归不再适用于此类变量之间相互关系的分析,需要将Pi转换成Pi=1的比例作为回归分析的因变量。而逻辑回归分析可解决此类问题,采用该分析方法能够确定在自变量Xn的作用下分类因变量Y发生的概率。假设P为模型响应概率,则逻辑回归模型可表示为如下形式:
![]()
(1)
式中:pi=P(yi=1∣x1, x2, …, xk) 为在给定系列自变量x1, x2, …, xk的值时的事件发生概率;βi为逻辑系数。只要有观测自变量x1至xk值组成的样本,以及事件是否发生的观测值,即可确定特定影响因素作用下事件的发生比以及发生的概率[14]。
本研究中的逻辑回归模型是通过统计分析软件SPSS中的二元Logistic回归分析操作建立的。
1.2.2 逐步回归分析
对于地下水污染程度的高低,可以用1个连续变量来表示,故可采用多元线性回归对地下水污染程度进行定量分析。逐步回归是1种常见的线性回归分析方法,其基本思想是将变量逐个引入模型,每引入1个自变量后,对已选入的变量进行逐个检验,当原先引入的变量由于后面变量的引入而变得不再显著时,要将其剔除。该过程反复进行,直到既无显著的自变量引入回归方程,也无不显著的自变量从回归方程中剔除为止,这样保证最终得到的为最优的回归方程。本研究中逐步回归的分析过程是通过SPSS软件中的线性回归分析操作完成的。
2 地下水污染预警模型建立
根据北京市平谷区平原地区第四系地层4个含水层组的地下水水质指标监测数据,首先运用逻辑回归分析建立各含水层组的地下水污染预测模型,判断地下水是否有受污染的可能,以GB/T 14848—93《地下水质量标准》中Ⅲ类地下水F值的上限值作为判定地下水是否污染的依据。若无受污染的可能,则定义地下水污染预警等级为零级,地下水水质状况较好,无需发布预警;若地下水有可能受到污染,则通过逐步回归分析计算各含水层组地下水污染预警指数,建立地下水污染预警等级评估模型。等级划分参照《国家突发环境事件应急预案》,将地下水污染预警等级从低到高划分为一级、二级、三级、四级。其中,一级预警表示地下水污染程度较低,水质有轻微的恶化趋势;二级预警表示地下水污染程度中等,水质存在一定的恶化趋势;三级预警表示地下水污染程度较高,水质恶化趋势较为严重;四级预警表示地下水污染程度很高,水质恶化趋势非常严重。
2.1 地下水污染预测逻辑回归模型
逻辑回归模型是用来确定在解释变量指标数值发生变化时地下水污染发生与否以及污染的发生比率。使用向后最大似然值筛选对模型影响较为显著的自变量指标,将筛选之后的自变量指标引入逻辑回归模型。各含水层组地下水中最终进入模型的水质指标见表1。可知:各含水层组地下水中对污染发生与否产生显著影响的指标大致相同,这反映了地下水污染由浅到深的变化过程。
模型检验结果显示,4个含水层组地下水污染预测逻辑回归模型的Cox & Snell R2分别为0.493、0.665、0.597、0.658,Nagelkerke R2分别为0.821、0.887、0.847、0.900,表明4个模型都具有很好的拟合度,即模型很好地拟合了监测数据。各含水层组地下水污染预测逻辑回归方程相关统计量见表1。
表1 各含水层组逻辑回归方程相关统计量
Table 1 Related statistics of logistic regression equations for each water bearing formation

含水层组自变量指标回归系数β标准误差Wald统计量自由度显著性Sig期望值Exp(β)第1含水层组常数-18.8485.25212.8771.000硫酸盐0.0650.0276.0011.00.0141.937氟化物7.2363.1015.4451.00.021388.584硝酸盐0.5920.15314.8861.001.807溶解性总固体0.0170.0093.7591.00.0531.018铁22.8696.38412.8311.008551447325第2含水层组常数-20.0314.95416.351.000氟化物8.0012.52410.0471.00.0022984.631硝酸盐0.3410.08316.8581.001.407铁13.5212.85822.3831.00744928.346总硬度0.0320.0110.9511.00.0011.032第3含水层组常数-13.7273.70713.7091.000氟化物9.7452.7312.7451.0017062.906硝酸盐0.4090.1398.6111.00.0031.505铁21.6436.06912.7181.002509164190氨氮10.3385.673.3241.00.06830875.538亚硝酸盐265.493100.2887.0081.00.0082.01E+115第4含水层组常数-41.78718.6934.9971.00.0250氟化物34.933 15.4775.0941.00.0241.483E+15硝酸盐1.68 0.7614.8681.00.0275.367铁34.8817.1544.1341.00.0421.40694E+15氯化物0.70.4812.1161.00.0461.497
由表1可看出:各含水层组地下水中铁和氟化物指标的Exp(β)值均达到较高的数量级,说明在研究区域内,这2项指标对污染发生与否的影响非常显著,当铁和氟化物的含量每增加1个单位浓度,地下水受污染的概率将远大于不受污染的概率。而在第3含水层组地下水中,氨氮含量变化的影响也十分明显,其污染发生比率高达30876。在第4含水层组地下水中,硝酸盐的影响较为明显,硝酸盐含量每增加1个单位浓度,地下水受污染的概率为未受污染概率的5.4倍。各含水层组地下水中其余主要影响指标作用下污染的发生比率均为1~2。
将自变量指标代入模型,对逻辑回归模型的预测效果进行评估,评估结果见表2。对于4个含水层组,地下水受污染的判对率分别为97.9%、91.8%、95.9%、97.1%,4个模型的预测准确率分别为94.7%、92.5%、93.3%、94.5%,表明所建模型的预测效果较好。
在SPSS软件中绘制逻辑回归模型的ROC曲线,对模型预测效果进行进一步评估,如图1所示。结果显示:4个模型的ROC面积均>0.98,且显著性均<0.05,表明与随机预测相比,模型可以显著提升预测准确率。
表2 各含水层组地下水污染预测逻辑回归模型预测效果
Table 2 Prediction effect of logistic regression models for groundwater pollution of each water bearing formation
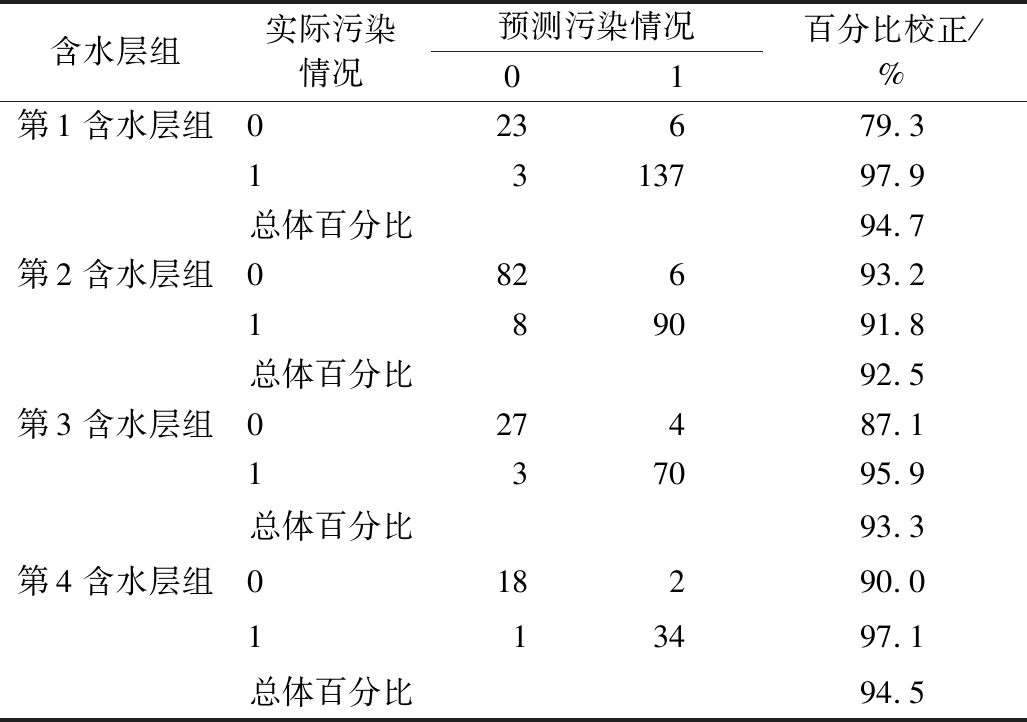
含水层组实际污染情况预测污染情况01百分比校正/%第1含水层组023679.31313797.9总体百分比94.7第2含水层组082693.2189091.8总体百分比92.5第3含水层组027487.1137095.9总体百分比93.3第4含水层组018290.0113497.1总体百分比94.5
注:0代表未受污染,1代表受污染。
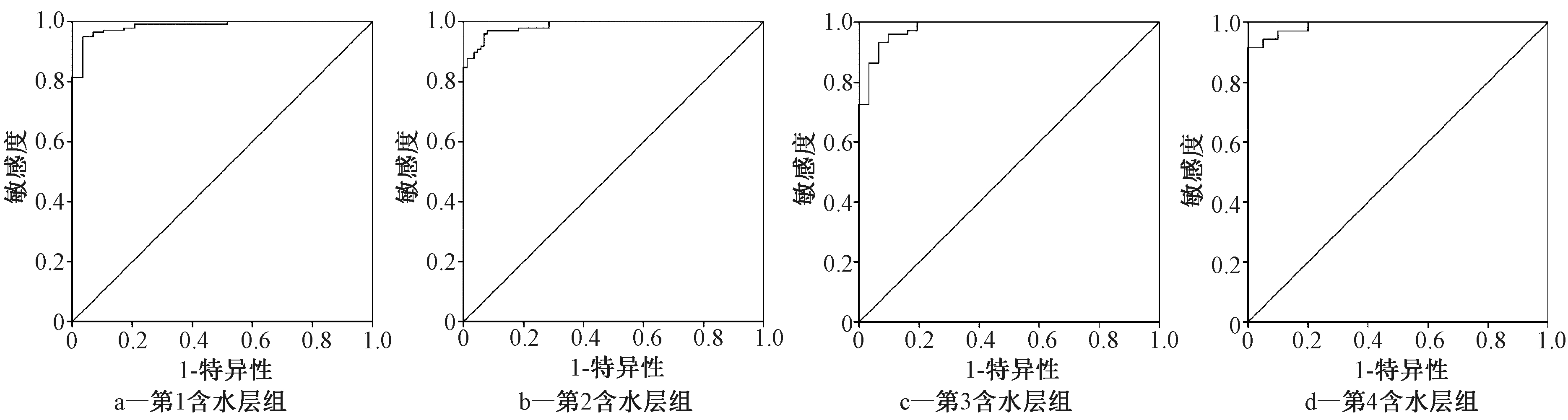
图1 各含水层地下水污染预测逻辑回归模型ROC曲线
Fig.1 ROC curves of logistic regression models for groundwater pollution prediction of each water bearing formation
综上,通过对4个含水层组中驱使地下水受污染的主要影响指标进行逻辑回归分析,可得到各含水层组地下水污染概率预测模型,具体表达式如下:
第1含水层组地下水污染概率为:
![]()
(2)
第2含水层组地下水污染概率为:
![]()
(3)
第3含水层组地下水污染概率为:
![]()
(4)
第4含水层组地下水污染概率为:
![]()
(5)
式中:各化学式代表地下水中该指标的含量。
2.2 地下水污染预警等级逐步回归模型
在通过逻辑回归分析确定地下水受污染的基础上,运用逐步回归对地下水污染程度进行定量分析。基于回归算法,逐步选取对污染程度影响较大的自变量指标,并建立地下水污染预警等级指数回归方程。各含水层组地下水中最终进入模型的水质指标见表3。可知:对污染程度影响较大的水质指标基本一致,同时反映了地下水污染由浅到深的变化过程;并且与逻辑回归分析得出的对污染发生与否产生显著影响的水质指标相近,也从侧面反映了分析结果的可靠性。
表3模型检验结果显示:4个含水层组地下水污染预警等级指数模型的拟合度分别为0.337、0.490、0.319、0.496,表明模型对因变量变异的拟合情况良好,且4个模型均通过了0.05的显著性检验。各含水层组地下水污染预警等级指数逐步回归方程的相关统计量见表3。
综上,通过对4个含水层组中影响地下水污染程度的主要水质指标进行逐步回归分析,可得到各含水层组地下水污染预警等级评估模型,具体表达式如下。
表3 各含水层组逐步回归方程相关统计量
Table 3 Related statistics of stepwise regression equations for each water bearing formation
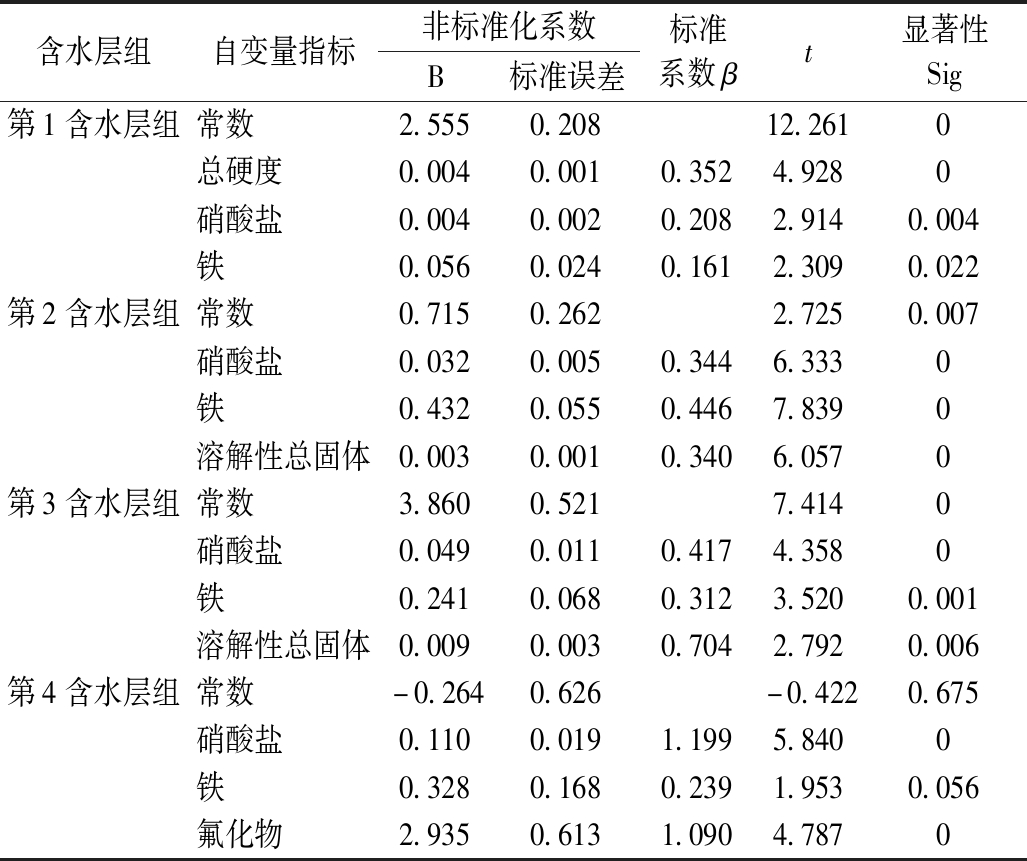
含水层组自变量指标非标准化系数B标准误差标准系数βt显著性Sig第1含水层组常数2.5550.20812.2610总硬度0.0040.0010.3524.9280硝酸盐0.0040.0020.2082.9140.004铁0.0560.0240.1612.3090.022第2含水层组常数0.7150.2622.7250.007硝酸盐0.0320.0050.3446.3330铁0.4320.0550.4467.8390溶解性总固体0.0030.0010.3406.0570第3含水层组常数3.8600.5217.4140硝酸盐0.0490.0110.4174.3580铁0.2410.0680.3123.5200.001溶解性总固体0.0090.0030.7042.7920.006第4含水层组常数-0.2640.626-0.4220.675硝酸盐0.1100.0191.1995.8400铁0.3280.1680.2391.9530.056氟化物2.9350.6131.0904.7870
第1含水层组地下水污染预警等级评估指数为:
y1=2.555+0.004总硬度![]()
(6)
第2含水层组地下水污染预警等级评估指数为:
![]()
(7)
第3含水层组地下水污染预警等级评估指数为:
![]()
(8)
第4含水层组地下水污染预警等级评估指数为:
![]()
(9)
式中:各化学式代表地下水中该指标的含量。
根据以上模型表达式计算2010—2017年各监测期次的地下水污染预警等级指数,并将计算结果与地下水质量综合评价结果进行对照分析,确定各含水层组地下水污染预警等级判据(表4)。
表4 各含水层组地下水污染预警等级指数范围
Table 4 Level index ranges of early warning for groundwater pollution of each water bearing formation

各含水层组预警级别第1含水层组第2含水层组第3含水层组第4含水层组一级<3.0<2.0<7.0<2.4二级3.0~3.42.0~2.57.0~7.52.4~2.8三级3.4~4.02.5~3.87.5~9.02.8~4.0四级>4.0>3.8>9.0>4.0
根据表4中的预警等级指数范围,可确定任一监测期次内4个含水层组的地下水污染预警等级,并将这4个含水层组中的最高预警级别确定为区域地下水污染预警等级。
3 结 论
本文以北京市平谷区平原地区第四系地层地下水水体为研究对象,利用各含水层组地下水水质指标监测数据,基于回归分析开展了地下水污染预警模型研究,主要结论如下:
1)回归分析方法可定量分析变量之间的变化规律和相互影响,可达到良好的预测效果,其在地下水污染预警方面的应用尚未见报道。
2)根据地下水水质状况和污染特征,参照国家相关标准和规定,将地下水污染预警等级划分为零级、一级、二级、三级、四级,对应的地下水污染程度分别为无污染、较低、中等、较高、很高。
3)对影响地下水污染发生与否的主要水质指标进行逻辑回归分析,结果表明:各含水层组地下水中对污染发生与否产生较大影响的指标基本一致,其中铁和氟化物的影响尤为显著。各含水层组地下水污染概率预测逻辑回归模型的伪R2均达到较高水平,模型很好地拟合了监测数据。模型对地下水污染发生的判对率和总体预测准确率均在90%以上,模型的预测效果较好。
4)通过逐步回归分析筛选各含水层组中对地下水污染程度影响较大的水质指标,结果表明,产生显著影响的指标基本一致。各含水层组的地下水污染预警等级指标模型拟合度均在0.3以上,模型拟合情况良好。根据所得模型可计算出地下水污染预警等级指数,进而得出预警等级指数范围,并据此确定区域地下水污染预警等级。
[1] 薛禹群,张幼宽. 地下水污染防治在我国水体污染控制与治理中的双重意义[J]. 环境科学学报, 2009, 29(3): 474-481.
[2] 白利平,孟凡生,王业耀,等. 地下水污染预警方法与示范[M]. 北京: 中国环境出版社, 2014.
[3] van der Schalie W H, Shedd T R, Knechtges P L,et al. Using higher organisms in biological early warning systems for real-time toxicity detection[J]. Biosensors & Bioelectronics, 2001, 16(7/8): 457-465.
[4] Martin L C,Abraham J M. Combined land-use and environmental factors for sustainable groundwater management[J]. Urban Water, 2001, 3(3): 229-237.
[5] Secunda S, Collin M L, Melloul A J. Groundwater vulnerability assessment using a composite model combining DRASTIC with extensive agricultural land use in Israel’s Sharon region[J]. Journal of Environmental Management, 1998, 54(1): 39-57.
[6] 洪梅,赵勇胜,张博. 地下水水质预警信息系统研究[J]. 吉林大学学报(地球科学版), 2002(4): 364-368,377.
[7] 张伟红. 地下水污染预警研究[D]. 长春:吉林大学, 2007.
[8] 谢洪波,钱壮志,尹国勋,等. 基于GIS的焦作市地下水污染预警系统[J]. 地球科学与环境学报, 2008(1): 94-96,106.
[9] 白利平,王业耀,郭永丽,等. 基于风险管理的区域(流域)地下水污染预警方法研究[J]. 环境科学, 2014, 35(8): 2903-2910.
[10] 何晓群,刘文卿. 应用回归分析[M]. 4版. 北京: 中国人民大学出版社, 2015.
[11] Oanh Nguyen Thi Kim,Ketsiri Leelasakultum. Analysis of meteorology and emission in haze episode prevalence over mountain-bounded region for early warning[J]. Science of the Total Environment, 2011, 409(11): 2261-2271.
[12] Li X J,Cheng Z W, Yu Q B,et al. Water-quality prediction using multimodal support vector regression: case study of Jialing River, China[J]. Journal of Environmental Engineering, 2017, 143(10):04017070.
[13] 北京市地质矿产勘查开发局,北京市水文地质工程地质大队. 北京地下水[M]. 北京: 中国大地出版社, 2008.
[14] Lemeshow S, Hosmer D W. Applied Regression Analysis[M]. New York: Wiley, 1989.