0 引 言
重金属污染是当前最严重的环境问题之一,在美国环境保护署的危险物质名录中(The ATSDR 2017 Substance Priority List),前10种化学品中重金属占了4种(As、Pb、Hg分列前3名,Cd列第7名)[1]。金属污染广泛存在于水体和土壤中,因其不可降解性及在土壤和水体沉积物中的高蓄积性,特别是对毒性较强的重金属的毒性预测和风险评估已成为当前水环境研究的热点问题之一[2, 3]。目前,重金属的生态风险涉及的评价标准在制定时仅仅是基于简单的暴露特征,如金属暴露浓度恒定不变,且以单一金属的毒性数据为基础,并没有考虑复杂的环境暴露特征,例如环境因素对金属生物毒性的影响,金属浓度随时间的变化,以及以复合态存在的金属的实测毒性。污染物的环境效应模型是环境基准和风险评估的基础和核心技术,目前常用的基于静态假设的浓度(剂量)-效应模型以及生物配体模型(biotic ligand model,BLM),存在无法揭示污染物的效应过程,不能描述金属随时间变化在生物体内的积累过程,也不能有效进行复杂暴露条件下的生态效应评估等不足。毒代-毒效动力学(toxicokinetic-toxicodynamic,TK-TD)模型适用于包含基于毒性机制的毒代动力学(毒物从外部到内部浓度)和毒效动力学(随时间变化的毒物内部浓度到毒性的发生)(图1)。与传统剂量-效应方法相比,TK-TD模型是实时预测毒性的有效方法,它可以从机理上将金属随时间变化在生物体内的积累与毒性联系在一起。并且TK-TD模型也是实验测试条件有效外推至其他实验条件的工具和方法。此外,利用此模型可以从实验数据解释毒性机制,进一步拓展了在有毒物质之间和物种之间进行毒性外推的可能性。本文介绍了TK-TD模型的基本概念、发展历程及模型构建的理论与方法,概述了TK-TD模型在水环境重金属毒性预测及风险评估中的研究进展和应用前景。
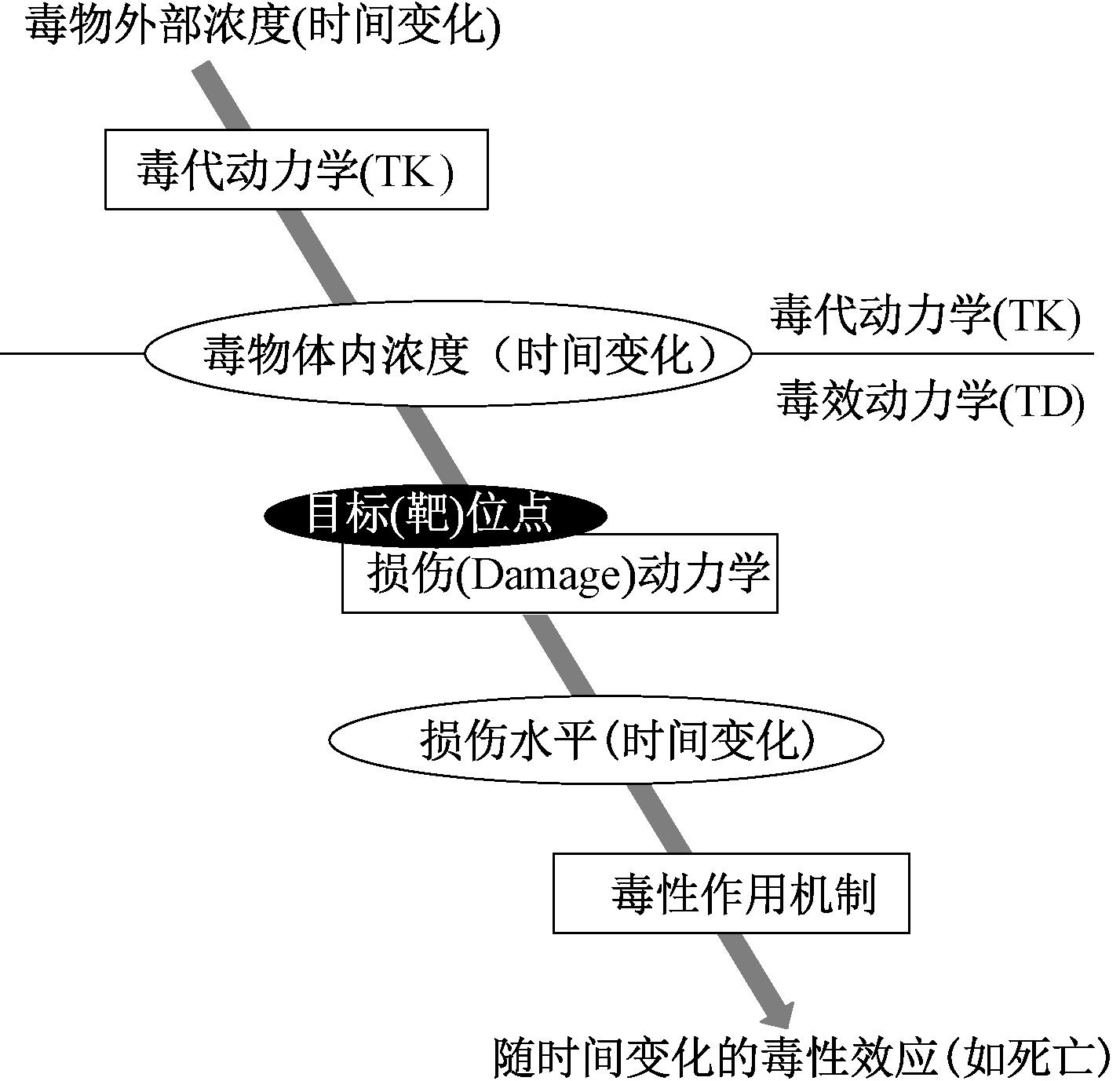
图1 毒代动力学和毒效动力学模型用于描述有毒物质外部浓度、体内浓度和毒性的时间变化过程[4]
Fig.1 Toxicokinetic and toxicodynamic models used to describe the time course of external concentrations, internal concentrations of toxic substances and subsequent toxicity
1 毒代动力学
1.1 污染物的毒代动力学过程
TK模型的基本假设是有毒物质首先需要被吸收到生物体内才能发挥作用[5]。一级动力学方程的单室TK模型假设生物体视为一个均质(充分混合)的隔室[6]。有毒物质从环境到生物体的吸收通量与外部浓度成比例,并且从生物体到环境的排泄通量与内部浓度成比例。有毒物质外部浓度不受生物体摄取的影响(环境无限大且充分混合)。但是某些情况下或数据有限时,需要使用更复杂的模型。例如,可以在方程中添加更多的隔室来代表生物体、代谢物或器官。但在实践中,实验数据的可获得性通常迫使我们使用简单的单室模型,具有一级动力学方程的一室模型通常用于有毒物质毒性预测风险评估中,并早在1924年就开始应用于化学物质的吸收和排出过程[6]。化学物质的吸收和排出过程既可以被视为独立的过程,也可以视为被动扩散方式达到相与相之间的平衡过程。
1.2 毒代动力学模型的分类
根据研究对象不同,TK模型可以分为分室TK模型和基于生理学的毒代动力学模型(physiologically based pharmacokinetic,PBPK)。分室TK模型可以分为一室和二室模型,一室模型将生物体的污染物看作1个整体,二室模型主要将生物体内的污染物分为代谢可利用态和解毒态。
1.2.1 分室TK模型的建立
传统的一室和二室TK模型用于表征污染物在生物体内的毒代动力学过程。通常,这类模型适用于具有单个器官的简单生物体,例如斑马鱼(Danio rerio)幼鱼[7]和大型溞(Daphnia magna)[8]。在建模时,生物体被视为一个整体,污染物在生物体内的平均浓度通过质量平衡方程估算,例如污染物的一阶吸收和消除动力学方程[9]。当需要对具有复杂动力学的污染物或者针对不同的物种进行种间毒性外推时,一室和二室TK模型并不适用。为了实现更为精确地进行污染物生态风险评价,有必要将更多的生物体组织器官作为单独的隔室(例如鳃、脑和肠道等),并准确定量研究污染物在组织、器官的浓度(剂量),最终实现污染物毒性的跨物种外推。
1.2.2 PBTK模型的建立
PBTK模型源于药物代谢动力学的研究。从20世纪80年代开始,PBTK模型开始逐渐被应用于毒理学的研究领域。PBTK模型是一种可用于描述生物体对污染物的吸收(absorption)、分布(distribution)、代谢(metabolism)和排泄(excretion)(统称ADME过程),并能够充分代表生物各个组织器官的内在联系和相互作用的多室模型。它将生物体分为多个通过流体(通常是血液)连接的真实组织或器官的隔室。PBTK模型结构在很大程度上取决于开发模型的目的和是否能获得足够的毒性数据。选择模型使其结构尽量简约是首要的指导原则。通常,PBTK模型结构仅包括描述化学物质及其代谢物的ADME过程的重要特征所必需的组织或器官,以及可能产生毒性的靶组织或器官。PBTK模型中的隔室被认为是均匀且完全混合的反应器。这意味着组织器官中的化学物质的浓度相同,并且通过分配系数与血液中化学物质的浓度建立定量关系[10]。
2 毒效动力学
2.1 污染物的毒效动力学过程
有毒物质在目标(靶)位点的浓度可能不足以解释毒性效应随时间的动态变化过程。因此,在毒效动力学(toxicodynamics,TD)模型中引入“损害”的概念[4]。有毒物质在生物体中的内部浓度可导致生物体内部的损伤,这种损伤也以一定速率修复。进一步,可以建立损伤程度与暴露效应终点之间的定量关系。以存活率为例,在TD过程中关于死亡机制有2种假设:一种假设是“个体耐受”(individual tolerance,IT,个体的敏感性不同),它基于个体对有毒物质的敏感性不同的假设,在某个时间点,死亡的个体比存活的个体更敏感。另一种假设是“随机死亡”(stochastic death,SD,死亡是一个随机过程,个体死亡概率是相同的),它假设毒物应激导致的生物死亡被视为一个随机过程,即每个个体都有相同的死亡机会,并且这种机会因暴露压力源的增加而增加[4]。
2.2 毒效动力学模型分类与建立
2.2.1 以死亡率为终点的GUTS模型
研究暴露时间和毒性效应关系时,最为突出的机理模型是临界体内残留(critical body residue,CBR)模型[11],如图2所示。它考虑了生物累积动力学和毒性之间的时间关系,适用于发生可逆作用的化学物质,如麻醉剂。麻醉剂一旦到达目标部位的生物膜,都会产生相同效应,破坏膜结构和扰乱膜功能的发挥[12]。CBR模型假定随时间变化的体内浓度决定毒性。然而,当化合物与特定的生物受体发生不可逆反应时,这个概念是不适用的。因此,CBR模型被进一步拓展为临界靶位点模型(critical target occupation,CTO)[13]。该模型假定当一定数量靶位点被不可逆占据时,生物会发生死亡。随后,CBR概念被进一步拓展为PULSETOX模型[14]和DEBtox[15, 16]急性毒性模型,它们认为毒性与超过体内无效应剂量(no-effect concentration,NEC)的量成正比。
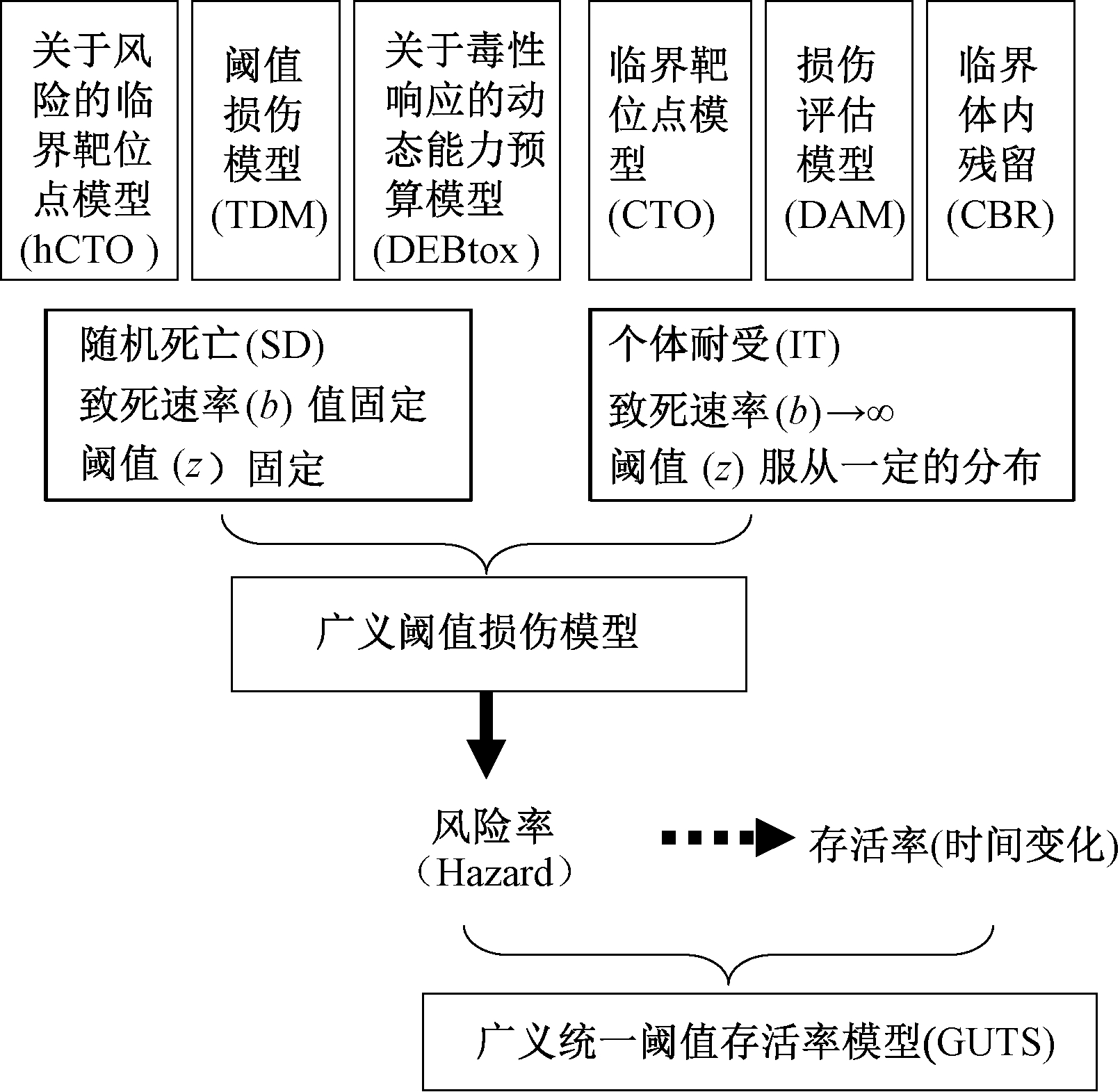
图2 TK-TD模型的发展历史[4]
Fig.2 Developing history of the TK-TD model
TK-TD模型取得突破性进展是在TK-TD模型中引入了状态变量-损伤(描述系统属性随时间变化的变量)[17]。基于损伤变量的TD模型被进一步发展成为损伤评估模型(damage assessment model,DAM)[18],该模型的基本假设是生物个体耐受性程度呈一定的概率分布[19]。DAM模型已被广泛用于拟合LC50值与暴露时间的关系[20]。虽然阈值损伤模型(threshold damage model,TDM)也在模拟毒性效应时使用损伤变量,但是它基于生物个体随机死亡的假设,并用于模拟毒物波动和反复脉冲暴露下生物体的存活率[21-23]。Jager等[4]将上述模型通过广义生存阈值模型(general unified threshold model of survival,GUTS)进行了统一,目前大多数的TK-TD模型都是基于此概念框架建立的。GUTS方程将污染物暴露剂量与生物存活联系起来,但是GUTS没有规定任何具体的污染物暴露剂量的度量(如体内浓度和外部浓度)。相反,GUTS提供了一个模型框架,以方便在模型中使用不同的剂量度量(毒物的外部浓度、毒物的内部浓度或损伤)[24]。
关于TK,最简单的GUTS版本采用一室模型并将外部浓度直接与比例损伤联系起来[4]。这种模型称为“简化版GUTS”(GUTS reduced,GUTS-RED),意味着主要速率常数kd(t-1)直接由原始观察到的存活数据确定(没有毒物内部浓度数据)。在这种情况下,基于动态过程描述损伤Dw(t)的微分方程如图3所示。在完整的GUTS框架内,模拟的毒物内部浓度与缩放的损伤相关联,假设损伤表示为Di(t)(例如以mol/kg为单位),根据内部浓度的增加而增加,并伴随个体以一定修复率常数kR(t-1)进行损伤修复。图3中,上图包括损伤动力学的2种微分方程,下图包括死亡机制(SD和IT)的2种微分方程。损伤动力学和死亡机制的组合衍生出GUTS-RED-SD、GUTS-RED-IT、GUTS-SD和GUTS-IT模型。
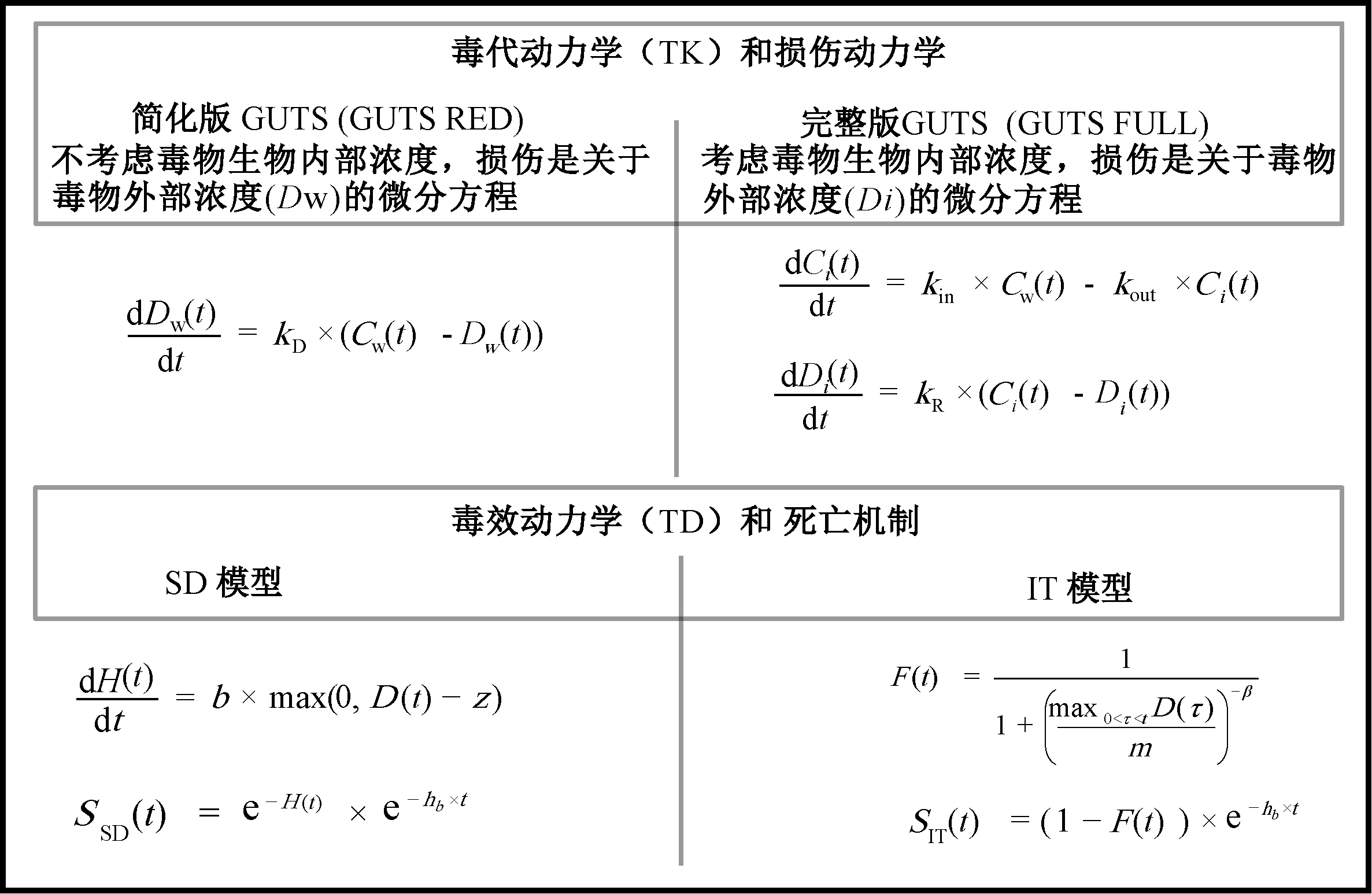
注:Dw(t)为缩放损伤,以浓度单位给出,例如以mol/L计;Cw为外部介质毒物浓度,例如以mol/L计;b为致死速率常数;z为内部阈值浓度;hb为背景死亡率常数;m为z分布的中值;β为分布的形状参数。
图3 关于GUTS-TKTD模型框架中使用的毒代动力学(TK)、损伤动力学和毒效动力学(TD)模型(随机死亡(SD)和个体耐受性(IT))的概述[4]
Fig.3 An overview of the toxicokinetic (TK), damage kinetics, and toxicodynamics (TD) models (schoastic death (SD) and individual tolerance (IT)) used in the GUTS-TKTD model framework
关于TD,在SD模型中,根据微分方程计算危险率H(t),其中,当比例损伤超过内部阈值浓度z时,描述危险与致死率常数b成比例地增加。对于SD模型的参数估计,必须根据存活率数据估计致死速率常数b([D]-1t-1)和内部阈值浓度z([D]); [D]代表缩放伤害的单位。在模拟时间过程中参数值保持不变,TK和TD的过程由常微分方程实现。计算个体在时间t之前存活概率SSD(t)公式如图3所示。在IT模型中,根据功能给出的1组个体中阈值z的累积对数-logistic分布计算个体到时间t的存活率F(t)公式如图3所示。通过方程SIT(t)计算个体到时间t的存活率,如图3所示。在IT模型中,生存与最大比例损伤有关,而不是与实际损伤有关,由于死亡是不可逆转的,因此在毒物浓度降低的情况下,模拟生物的死亡率水平也不会再降低。
2.2.2 以亚急性指标为终点的DEB模型
基于动态能量预算(dynamic energy budget, DEB)理论的模型在分析和解释毒物对生长、繁殖和存活等生活史特征的影响方面具有重要优势[25-27]。与传统剂量-效应方法相比,基于DEB理论的分析可以在1个框架中使用所有数据(所有时间点和所有端点),并产生可以在毒物之间进行比较的与时间无关的毒性效应[28]。该理论提供了毒物对各种暴露终点的影响之间的联系,这对于从种群水平评价毒物产生的毒性是必不可少的[29-31],并可以解释毒物对基因表达水平的影响[32]。此外,DEB概念很容易扩展到毒物浓度随时间变化[33]和毒物以混合物形式存在的暴露特征[34]。基本原则是毒物一旦被摄入体内,就会影响生物体获取和/或使用能量。标准DEB模型适用于以1种食物为能量摄取来源的动物,并且这种能量来源在其生命周期中不会改变其形状(同形体)。其生物质由结构(需要维护)能量和储备能量(可以促进代谢过程)2种成分组成,每种成分恒定不变[35]。能量流即食物被生物体吸收,部分能量被同化为储备能量。储备能量分成2个部分:一部分到躯体,另一部分到成熟和繁殖。首先必须满足体细胞维护所需能量,并且剩余的能量可以用于体细胞生长。同样,也必须满足成熟度维持的能量,其余能量用于成熟(胚胎和幼体)或繁殖(成年人)。DEB模型中的有些状态变量无法直接测量,需要辅助理论将模型属性与可观察变量联系起来。例如,生物体的物理尺寸包含来自储备能量、结构能量和可能的再生缓冲物的能量[25-27]。DEBtox的方程式[36]通过重新参数化(从模型系统中去除能量的维度)以及使用3个额外的假设从完整的标准模型得出:第1个假设是成熟度始终是结构能量的1个固定比例(对于胚胎和青少年)。第2个假设是卵的能量需求在所有情况下都是恒定的。这与DEB理论中的“母体效应”,其中卵的能量取决于母本的状态(营养状态和身体对毒物的负荷)形成鲜明对比。第3个假设是储备能量总是与食物水平处于稳定状态。目前已经有研究通过DEBtox模型研究了重金属对藻类生长的抑制效应[35, 39]及建立了可靠的剂量-效应关系[37, 38]。
3 毒代-毒效动力学模型在金属水生态风险评估中的应用
3.1 TK-TD用于金属水生态风险评估的基本过程
生态风险评价的效应评估包括多层级的评估方法(图4)。第1层次评估是基于标准单一物种测试数据计算评价标准限值。更高层的评估包括多种实验方法,其中,第2层次Tier-2A评估中,增加其他测试物种,通过几何平均法和证据权重分析法(weight of evidence,WoE)来计算评价标准限值[40];第2层次Tier-2B评估中,通过物种敏感分布法(species sensitivity distribution,SSD法)计算评价标准限值;Tier-2C评估中,通过TK-TD模型计算污染物的LC50来修正评价标准限值;第3层Tier-3评估中,从种群、群落水平上模拟污染物暴露特征;第4层Tier-4评估中,模拟实际环境中污染物暴露特征。

图4 生态风险评价的效应评估包括多层级的评估方法[20]
Fig.4 Effect assessment of ecological risk assessment including multi-tier assessment methods
在金属水环境生态风险评估中,运用TK-TD模型可以定量预测污染物的毒性效应,明确金属暴露特征随时间变化下,在个体水平上的毒性效应与金属在体内的积累量的定量关系。其次,TK-TD模型是基于物种特征参数(如吸收速率和络合常数)和暴露条件(金属浓度、金属化学形态,发生相互作用金属的浓度和暴露时间)下建立的,可以外推不同生物和不同空间、时间尺度下金属暴露的剂量-效应关系[41]。并且TK-TD模型可用于预测金属暴露特征随时间变化下,对个体的致死和/亚致死效应(包括水生无脊椎动物的损伤修复)。在应用TKTD模型时,需要重点考虑的问题在于选择建模的物种,确定可能在急性和慢性风险中处于危险的水生生物类群[42]。
在Tier-1评估中,标准单一水生物种的急性和慢性毒性数据可直接用TK-TD模型加以验证。其基本过程是由相关水生生物物种的毒性数据得出污染物预测环境浓度值(predicted environmental concentration,PEC),并进一步得出相应的污染物可接受浓度值(regulatory acceptable concentration,RAC),将两者加以比较,确定所关注金属是否触发环境风险。在Tier-2A和Tier-2B评估过程中,由标准水生物种的毒性数据即96 h-EC50通过几何平均法(或WoE法)和SSD方法计算得出相对应的RAC值,并将其与PEC值进行比较,判断所关注的金属在暴露场地引发环境风险的可能性。在Tier-2C1评价方法中,基于水生测试物种的毒性数据,使用验证TK-TD模型建立的剂量-效应曲线计算引起x%生物死亡(或不良反应)的污染物暴露情景(lethal profile,LPx,或effective profile,EPx)。将所有相关水生物种的LP50/EP50值与急性和慢性的相关评估因子(assessment factor,AF)值进行比较,确定该金属在环境中的风险高低。对Tier-2C2而言,根据毒性测试水生物种种类不同有不同的评价方法,例如,对于少于8种水生无脊椎动物和/或初级生产者或少于5种鱼类的毒性数据,通过TK-TD模型计算不同物种的LP50/EP50/EP10值,并采用几何平均方法(目前主要用于污染物急性风险评价)和/或WoE方法得出RAC值;对于有8种以上水生无脊椎动物和/或初级生产者或5种以上鱼类的毒性数据,通过TK-TD模型计算不同物种的LP50/EP50/EP10值,采用SSD方法得到污染物的HP5,将2种情况得出的毒性数据与相应的AF值进行比较,确定污染物引发潜在环境风险的可能性。总之,基于金属暴露过程的TK-TD模型可以定量研究金属对水生生物的毒性,将金属污染物连续监测数据作为模型输入变量,实时模拟金属有害生态效应,最终确定金属对水生生物没有毒害的安全阈值。
3.2 在金属脉冲暴露情景风险评估中的应用
在现实环境中,由于人类活动(如工业污染的间断式排放、泄漏等)的影响使得水生生态系统内部可能在固定时间点或非固定时间点发生突变,而这些突变持续的时间和整个环境系统的持续时间相比非常短暂,所以把人类活动的连续干扰当作离散的脉冲干扰会更加符合实际环境[43, 44]。关于重金属脉冲暴露的研究很少。Hoang等[45]研究Sn和Se的持续暴露和脉冲暴露对大型溞的影响,发现持续暴露的毒性高于脉冲暴露的毒性,然而Nyman等[46]发现脉冲暴露比持续暴露产生的毒性更大。但是这些研究没有对毒性进行量化,缺乏模型理论的支持。
脉冲暴露的分析在实验[47]和建模[5, 46, 48]相结合的研究中越来越受关注。目前常使用模型来模拟污染物对生物产生毒性的过程,大部分模型只考虑了生物效应的结果,而忽略了过程。然而,动力学模型不仅考虑毒性终点,同时还考虑时间因素,从而可更清楚地了解毒性机制[6]。Hickie等[49]首次利用一级动力学模型建立了一个基于毒物体内残留量的脉冲暴露效应模型。Hoang等[45]分别研究了Cu、Zn和Sn在脉冲和持续暴露下的毒性影响,并建立了污染物一级动力学吸收方程,但是这个方程只考虑暴露时间、暴露浓度以及脉冲间隔等因素,没有考虑毒性随时间的变化过程。TK-TD模型可以实时地模拟毒物进入生物体内并产生毒性的一系列过程,同时还考虑时间变量。Widianarko等[50]研究孔雀鱼在重金属Zn的脉冲暴露下的毒代动力学过程,发现孔雀鱼清除毒物的速率(0.434~0.488/d)与在Zn持续暴露下的清除速率(0.463/d)相当接近,提出脉冲暴露的毒性试验可以代替传统的持续暴露实验。Chen等[51]基于TK-TD模型来预测水环境中重金属Cd和Pb脉冲暴露对斑马鱼的毒性影响,发现TK-TD模型可以解释和预测重金属在不同脉冲暴露下生物体内的积累和产生毒性的过程,可以用来预测和评估自然水体中重金属的毒性和生态风险。目前的研究表明,TK-TD模型在污染物波动或脉冲暴露下的风险评估方面具有很大的应用潜力。
3.3 在金属混合物风险评估中的应用
在实际环境中,金属元素通常以混合物的形式存在。当金属混合物通过同一摄取途径进入生物体内,金属之间的相互作用影响其生物摄取、累积及毒性。金属混合暴露与金属单独暴露生物产生的毒性完全不同,通常表现出不同的联合毒性效应,如协同、拮抗、加和和独立作用[52]。有报道指出大多数的金属在相互作用时表现出加和毒性作用[53]。长期以来被广泛应用于混合污染物的毒性预测和风险评价的浓度加和(concentration addition, CA)模型和效应加和(independent addition, IA)模型及其衍生模型(毒性单元法TU、毒性当量TEQ及CA+IA两步预测法等)的普适性正受到质疑,特别是针对金属混合物毒性的预测[54]。首先,这类模型是基于无相互作用这个基本假设。其次,这类模型没有考虑金属从暴露到效应的具体生物化学过程与金属暴露的时间维度[55]。而考虑金属联合毒性预测目前最具代表性的生物配体模型(biotic ligand model,BLM),已广泛应用于定量评价水生态系统中水化学条件对金属形态和生物有效性的影响[56],但其只关注暴露浓度与效应终点的量效关系,而对于金属进入体内以后的分布、转化、排出(TK过程)及毒效过程(TD过程)的相互作用并未考虑,同时也没有考虑毒性的时间过程,因此无法解释和预测动态的金属积累与毒性过程。这意味着目前所采用的这几类模型可能会高估或低估金属混合物的毒性。
目前运用TK-TD模型预测金属联合毒性的研究才刚刚起步。Wang等[57]尝试建立金属混合物对大型溞(Daphnia Magna)的TK过程的联合作用模型。Gao等[58]也初步建立了利用单一金属参数预测具有相加或拮抗效应的金属混合物在斑马鱼幼鱼体内积累量的TK模型。Tan等[59]在金属浓度高度动态变化的河口环境下,运用TK模型预测多种重金属在牡蛎体内积累过程中的相互作用。Margerit等[60]和Jager等[61]基于动态能量预算理论建立TK-TD模型来预测金属混合物对线虫的联合毒性。尽管这些模型可以较好地模拟和预测联合暴露下金属在生物体内的累积过程,但对于毒性的预测仍存在较大误差[62]。目前TK-TD模型对于具有协同或独立作用的金属混合物毒性预测方面具有一定局限性,其主要原因在于对于金属在生物体内分布、转化、代谢过程及毒性发生过程中可能存在的相互作用机理理解有限。因此,提高TK-TD模型对金属混合物毒性预测的准确性,除了关注混合物对个体水平的毒效指标,还需要进一步研究在分子水平上存在的稳定量效关系的毒效指标,即分子起始事件,并且将其进一步量化到模型中。
3.4 应用TK-TD模型外推至未经测试的金属和物种的风险评估
在评估化学品风险时,通常通过毒性差异来划分具有相似特性的化学物质(相似的模型参数)。TK-TD模型提供了这种方法的概念框架[34]。化合物化学特性影响TK过程,例如,化合物物理化学性质影响生物转化方式。化合物化学特性也可以影响TD模型,例如该化合物物理化学性质影响潜在的毒性效应(不考虑生物累积潜力的影响)和致毒机制(图5)。故化合物的化学特性是同时影响TK(如发生反应的化学物质)和TD(如化学物质的毒性潜力由它们对生物体内核物质的亲和性决定[63])过程的重要参数。如果TK和TD模型参数之间的定量关系可以确定,那么模型可以用来预测未测试化合物的毒性。模型参数和化合物化学性质之间的定量关系可以通过查阅文献资料获得。运用TK模型对金属生物累积的评估已取得了一定的进展[64],并且物种或化合物的相关关系已经确立[65],但对于TD模型,还没有确立物种或化合物的相关关系。我们认为,TK-TD框架将有助于建立这一缺失的环节,特别是因为TK-TD模型建立在机理性的认识基础之上,例如化合物毒性作用机制。
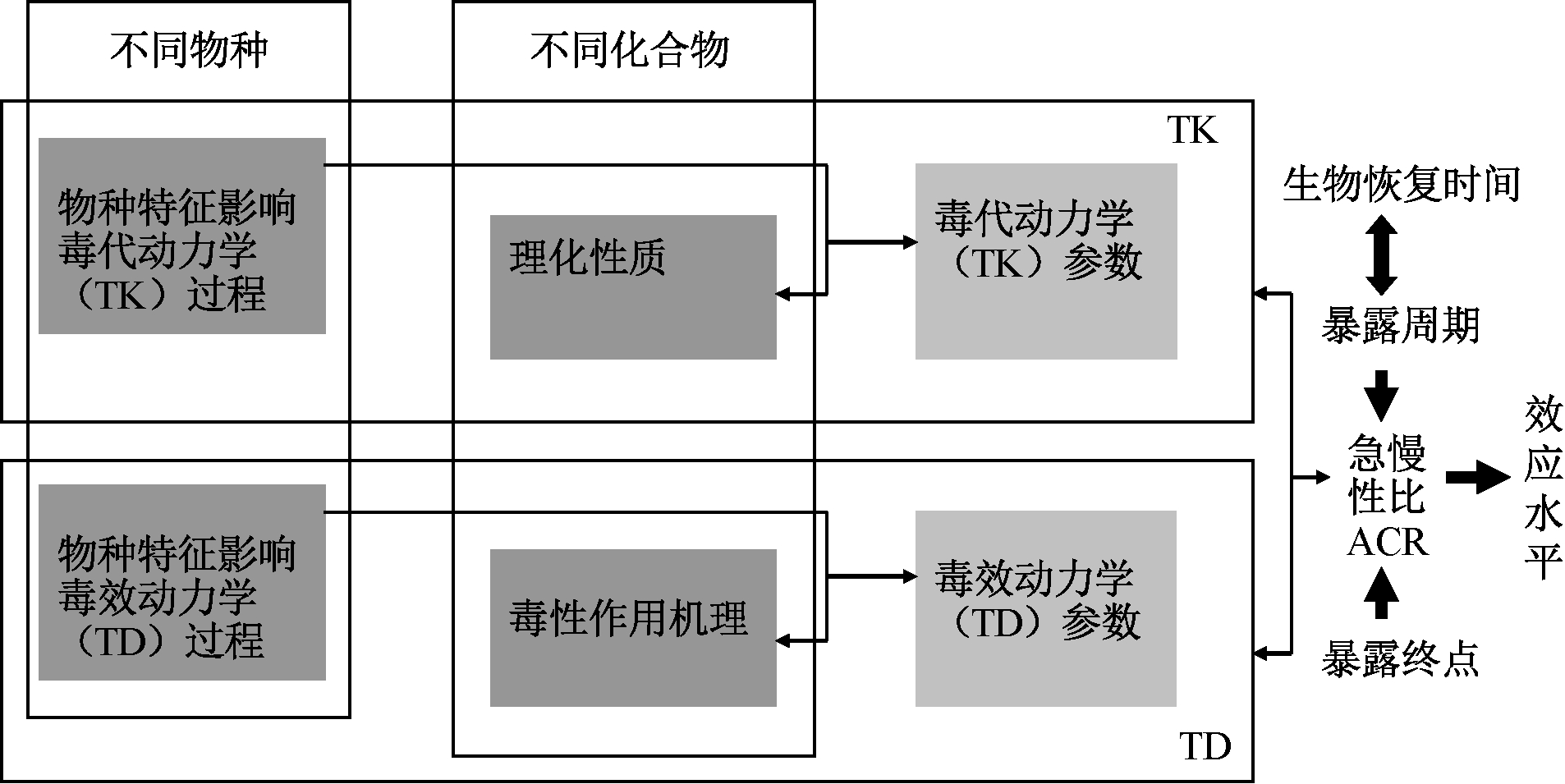
图5 化合物和物种特性对TK-TD模型的参数的影响[6]
Fig.5 Effect of characteristics of compound and species on parameters in the TK-TD model
没有全面理解物种敏感度差异阻碍了人类保护生物物种的进程。TK-TD模型可系统地了解哪些物种性状(物种的属性)可以建立在TK和TD(图5)的概念框架中[66]。如果可以明确物种性状和TK模型或TD模型参数之间的定量关系,则模型可以用来预测化合物对未测试物种的毒性效应[66]。目前对于TK模型参数和物种特征参数间的关系比TD模型和物种特征参数间的关系有了一定的了解[65, 67]。在TK-TD模型框架内调查物种敏感度差异,有助于理解基本生态毒理现象的系统性方法(即为什么各个物种敏感性不同),因为它可以为模型毒性外推至未经测试物种提供基础数据。
4 研究展望
作为机理过程效应模型,TK-TD模型可以解释多因素影响下污染物的毒性效应机理,模拟和预测复杂暴露条件下污染物对于生物的效应过程。目前TK-TD模型已被纳入OECD/ISO指南以分析剂量-效应数据[68],EFSA也将其作为植物保护产品Tier-2级风险评估的补充方法[40]。但目前TK-TD模型在金属水生态风险评估的理论与技术方法上还存在一些局限,这也是未来需要重点解决的问题。
1)目前重金属的TK-TD模型框架体系中,TK过程及其模型比较清晰和成熟。相对而言,TD过程的研究才刚开始展开,特别是对于亚急性指标为毒性效应终点的TD模型目前还很缺乏,从而限制了对实际环境浓度下污染物效应的定量预测和评估。
2)环境介质中金属浓度随时间而变化,风险评估中往往考虑短期内时间加权平均浓度,期望通过TK-TD模型模拟环境中金属浓度随时间变化使得金属风险评估结果更可靠。
3)所有环境介质都含有天然存在的金属混合物,自然环境中金属的联合毒性预测一直是生态毒理学研究领域的难点和热点,构建考虑金属联合作用的TK-TD毒性预测模型将有助于实际环境中混合污染物的风险评估。
4)金属生物有效性受到环境化学条件的强烈影响,如何将这些影响整合到目前的TK-TD模型框架中,从而更准确地进行实际环境中的金属毒性预测和风险评估将是未来的一个重要挑战。
[1] Cao H C, Luan Z Q, Wang J D, et al. Potential ecological risk of cadmium, lead and arsenic in agricultural black soil in Jilin Province, China [J]. Stochastic Environmental Research and Risk Assessment, 2009, 23(1): 57-64.
[2] Gao X, Zhou F, Chen C T A. Pollution status of the Bohai Sea: an overview of the environmental quality assessment related trace metals [J]. Environment International, 2014, 62(1):12-30.
[3] Jin L, Liu J, Ye B, et al. Concentrations of selected heavy metals in maternal blood and associated factors in rural areas in Shanxi Province, China [J]. Environment International, 2014, 66(1):57-64.
[4] Jager T, Albert C, Preuss T G, et al. General unified threshold model of survival:a toxicokinetic-toxicodynamic framework for ecotoxicology [J]. Environmental Science & Technology, 2011, 45(7): 2529-2540.
[5] Ashauer R. Toxicokinetic-toxicodynamic modelling in an individual based context: consequences of parameter variability [J]. Ecological Modelling, 2010, 221(9): 1325-1328.
[6] Ashauer R, Escher B I. Advantages of toxicokinetic and toxicodynamic modelling in aquatic ecotoxicology and risk assessment [J]. Journal of Environmental Monitoring, 2010, 12(11): 2056-2061.
[7] Gao Y F, Feng J F, Zhu L. Prediction of acute toxicity of cadmium and lead to zebrafish larvae by using a refined toxicokinetic-toxicodynamic model [J]. Aquatic Toxicology, 2015, 169(1):37-45.
[8] Tan Q G, Wang W X. Two-compartment toxicokinetic-toxicodynamic model to predict metal toxicity in Daphnia magna [J]. Environmental Science & Technology, 2012, 46(17): 9709-9715.
[9] Luoma S N, Rainbow P S. Why is metal bioaccumulation so variable? Biodynamics as a unifying concept [J]. Environmental Science & Technology, 2005, 39(7): 1921-1931.
[10] Grech A, Tebby C, Brochot C, et al. Generic physiologically-based toxicokinetic modelling for fish: integration of environmental factors and species variability [J]. Science of the Total Environment, 2019, 651(5):16-31.
[11] Wen Y M, Su L C, Qin W, et al. Investigation of critical body residues and modes of toxic action based on injection and aquatic exposure in fish [J]. Water Air and Soil Pollution, 2015, 226(6):23-41.
[12] Escher B I, Hermens J L M. Modes of action in ecotoxicology: their role in body burdens, species sensitivity, QSARs, and mixture effects [J]. Environmental Science & Technology, 2002, 36(20): 4201-4217.
[13] Legierse K, Verhaar H J M, Vaes W H J, et al. Analysis of the time-dependent acute aquatic toxicity of organophosphorus pesticides: the critical target occupation model [J]. Environmental Science & Technology, 1999, 33(6): 917-925.
[14] Reinert K H, Giddings J A, Judd L. Effects analysis of time-varying or repeated exposures in aquatic ecological risk assessment of agrochemicals [J]. Environmental Toxicology and Chemistry, 2002, 21(9): 1977-1992.
[15] Pery A R R, Ducrot V, Mons R, et al. Survival tests with Chironomus riparius exposed to spiked sediments can profit from DEBtox model [J]. Water Research, 2003, 37(11): 2691-2699.
[16] Pery A R R, Flammarion P, Vollat B, et al. Using a biology-based model (DEBtox) to analyze bioassays in ecotoxicology: opportunities and recommendations [J]. Environmental Toxicology and Chemistry, 2002, 21(2): 459-465.
[17] Ankley G T, Erickson R J, Phipps G L, et al. Effects of light intensity on the phototoxicity of fluoranthene to a benthic macroinvertebrate [J]. Environmental Science & Technology, 1995, 29(11): 2828-2833.
[18] Lee J H, Landrum P F, Koh C H. Prediction of time-dependent PAH toxicity in Hyalella azteca using a damage assessment model [J]. Environmental Science & Technology, 2002, 36(14): 3131-3138.
[19] Zhao Y, Newman M C. The theory underlying dose-response models influences predictions for intermittent exposures [J]. Environmental Toxicology and Chemistry, 2007, 26(3): 543-547.
[20] Butcher J, Diamond J, Bearr J, et al. Toxicity models of pulsed copper exposure to Pimephales promelas and Daphnia magna [J]. Environmental Toxicology and Chemistry, 2006, 25(9): 2541-2550.
[21] Ashauer R, Boxall A B A, Brown C D. Modeling combined effects of pulsed exposure to carbaryl and chlorpyrifos on Gammarus pulex [J]. Environmental Science & Technology, 2007, 41(15): 5535-5541.
[22] Ashauer R, Hintermeister A, Caravatti I, et al. Toxicokinetic and toxicodynamic modeling explains carry-over toxicity from exposure to diazinon by slow organism recovery [J]. Environmental Science & Technology, 2010, 44(10): 3963-3971.
[23] Ashauer R, Boxall A B A, Brown C D. Simulating toxicity of carbaryl to Gammarus pulex after sequential pulsed exposure [J]. Environmental Science & Technology, 2007, 41(15): 5528-5534.
[24] Ashauer R, Albert C, Augustine S, et al. Modelling survival: exposure pattern, species sensitivity and uncertainty [J]. Scientific Reports, 2016, 6:29178.
[25] Smallegange I M, Caswell H, Toorians M E M, et al. Mechanistic description of population dynamics using dynamic energy budget theory incorporated into integral projection models [J]. Methods in Ecology and Evolution, 2017, 8(2): 146-154.
[26] Yoann T, Jonathan F S M, Denis C, et al. Effects of of hypoxia on metabolic functions in marine organisms: observed patterns and modelling assumptions within the context of dynamic energy budget (DEB) theory [J]. Journal of Sea Research, 2019, 143(2):31-42.
[27] Galic N, Forbes V E. The role of dynamic energy budget theory in predictive modeling of stressor impacts on ecological systems comment on: “physics of metabolic organization” by marko jusup et al [J]. Physics of Life Reviews, 2017, 20(4):43-45.
[28] Billoir E, Delignette-Muller M L, Pery A R R, et al. Statistical cautions when estimating DEBtox parameters [J]. Journal of Theoretical Biology, 2008, 254(1): 55-64.
[29] Martin B T, Jager T, Nisbet R M, et al. Extrapolating ecotoxicological effects from individuals to populations: a generic approach based on Dynamic Energy Budget theory and individual-based modeling [J]. Ecotoxicology, 2013, 22(3): 574-583.
[30] Jager T, Klok C. Extrapolating toxic effects on individuals to the population level: the role of dynamic energy budgets [J]. Philosophical Transactions of the Royal Society B-Biological Sciences, 2010, 365(1557): 3531-3540.
[31] Klaniscek T, Caswell H, Neubert M G, et al. Integrating dynamic energy budgets into matrix population models [J]. Ecological Modelling, 2006, 196(3/4): 407-420.
[32] Swain S, Wren J F, Stuerzenbaum S R, et al. Linking toxicant physiological mode of action with induced gene expression changes in Caenorhabditis elegans [J]. Bmc Systems Biology, 2010, 4(1):1-19.
[33] Pieters B J, Jager T, Kraak M H S, et al. Modeling responses of Daphnia magna to pesticide pulse exposure under varying food conditions: intrinsic versus apparent sensitivity [J]. Ecotoxicology, 2006, 15(7): 601-608.
[34] Jager T, Kooijman S A L M. A biology-based approach for quantitative structure-activity relationships (QSARs) in ecotoxicity [J]. Ecotoxicology, 2009, 18(2): 187-196.
[35] Jager T, Zimmer E I. Simplified dynamic energy budget model for analysing ecotoxicity data [J]. Ecological Modelling, 2012, 225(1):74-81.
[36] Kooijman S A L M, Bedaux J J M. Analysis of toxicity tests on Daphnia survival and reproduction [J]. Water Research, 1996, 30(7): 1711-1723.
[37] Miller R J, Muller E B, Cole B, et al. Photosynthetic efficiency predicts toxic effects of metal nanomaterials in phytoplankton [J]. Aquatic Toxicology, 2017, 183(2):85-93.
[38] Xie M D, Sun Y X, Feng J F, et al. Predicting the toxic effects of Cu and Cd on Chlamydomonas reinhardtii with a DEBtox model [J]. Aquatic Toxicology, 2019, 210(10):6-16.
[39] Kooijman S A L M, Sousa T, Pecquerie L, et al. From food-dependent statistics to metabolic parameters, a practical guide to the use of dynamic energy budget theory [J]. Biological Reviews of the Combridge Philosophical Society, 2008, 83(4): 533-552.
[40] None. Guidance on tiered risk assessment for plant protection products for aquatic organisms in edge-of-field surface waters [J]. EFSA Journal, 2013, 11(7): 3290.
[41] Hommen U, Schmitt W, Heine S, et al. How TK-TD and population models for aquatic macrophytes could support the risk assessment for plant protection products [J]. Integr Environ Assess Manag, 2016, 12(1): 82-95.
[42] Ockleford C, Adriaanse P, Berny P, et al. Scientific Opinion on the state of the art of Toxicokinetic/Toxicodynamic (TKTD) effect models for regulatory risk assessment of pesticides for aquatic organisms [J]. EFSA Journal, 2018, 16(8):1-8.
[43] Ashauer R, Boxall A B A, Brown C D. New ecotoxicological model to simulate survival of aquatic invertebrates after exposure to fluctuating and sequential pulses of pesticides [J]. Environmental Science & Technology, 2007, 41(4): 1480-1486.
[44] Duruibe J O, Ogwuegbu M O C, Egwurugwu J N. Heavy metal pollution and human biotoxic effects [J]. International Journal of the Physical Sciences, 2007, 2(5): 112-118.
[45] Hoang T, Tomasso J, Klaine S. An integrated model describing the toxic responses of Daphnia magna to pulsed exposures of three metals[J]. Environmental Toxicology and Chemistry, 2007, 26(10): 2247-2254.
[46] Nyman A-M, Schirmer K, Ashauer R. Toxicokinetic-toxicodynamic modelling of survival of Gammarus pulex in multiple pulse exposures to propiconazole: model assumptions, calibration data requirements and predictive power [J]. Ecotoxicology, 2012, 21(7): 1828-1840.
[47] Pery A R R, Bedaux J J M, Zonneveld C, et al. Analysis of bioassays with time-varying concentrations [J]. Water Research, 2001, 35(16): 3825-3832.
[48] Ashauer R, Thorbek P, Warinton J S, et al. A method to predict and understand fish survival under dynamic chemical stress using standard ecotoxicity data [J]. Environmental Toxicology and Chemistry, 2013, 32(4): 954-965.
[49] Hickie B E M L S, Dixon G D. A residue-based toxicokinetic model for pulse-exposure toxicity in aquatic system [J]. Environmental Toxicology & Chemistry. 1995, 32(2): 2187-2197.
[50] Widianarko B, Kuntoro F X S, van Gestel C A M, et al. Toxicokinetics and toxicity of zinc under time-varying exposure in the guppy (Poecilia reticulata) [J]. Environmental Toxicology and Chemistry, 2001, 20(4): 763-768.
[51] Chen M, Gao Y F, Bian X X, et al. Predicting the survival of zebrafish larvae exposed to fluctuating pulses of lead and cadmium [J]. Chemosphere, 2019, 223(2):599-607.
[52] Komjarova I, Blust R. Multimetal Interactions between Cd, Cu, Ni, Pb, and Zn uptake from water in the zebrafish danio rerio [J]. Environmental Science Technology, 2009, 43(19): 7225-7229.
[53] Norwood W P, Borgmann U, Dixon D G, et al. Effects of metal mixtures on aquatic biota: a review of observations and methods [J]. Human and Ecological Risk Assessment, 2003, 9(4): 795-811.
[54] Vijver M G, Elliott E G, Peijnenburg W J G M, et al. Response predictions for organisms water-exposed to metal mixtures: a meta-analysis [J]. Environmental Toxicology and Chemistry, 2011, 30(6): 1482-1487.
[55] Baas J, Van Houte B P P, van Gestel C A M, et al. Modeling the effects of binary mixtures on survival in time [J]. Environmental Toxicology and Chemistry, 2007, 26(6): 1320-1327.
[56] Paquin P R, Gorsuch J W, Apte S, et al. The biotic ligand model: a historical overview [J]. Comparative Biochemistry and Physiology C-Toxicology & Pharmacology, 2002, 133(1/2): 3-35.
[57] Wang X R, Liu J P, Tan Q G, et al. Development of multi-metal interaction model for Daphnia magna: significance of metallothionein in cellular redistribution [J]. Ecotoxicology and Environmental Safety, 2018, 151(4):2-8.
[58] Gao Y F, Feng J F, Kang L L, et al. Concentration addition and independent action model: which is better in predicting the toxicity for metal mixtures on zebrafish larvae [J]. Science of the Total Environment, 2018, 610/611:442-450.
[59] Tan Q G, Zhou W, Wang W X. Modeling the toxicokinetics of multiple metals in the oyster crassostrea hongkongensis in a dynamic estuarine environment [J]. Environmental Science & Technology, 2018, 52(2): 484-492.
[60] Margerit A, Gomez E, Gilbin R. Dynamic energy-based modeling of uranium and cadmium joint toxicity to Caenorhabditis elegans [J]. Chemosphere, 2016, 146(40):5-12.
[61] Jager T, Gudmundsdottir E M, Cedergreen N. Dynamic modeling of sublethal mixture toxicity in the nematode Caenorhabditis elegans [J]. Environmental Science & Technology, 2014, 48(12): 7026-7033.
[62] Gao Y F, Feng J F, Han F, et al. Application of biotic ligand and toxicokinetic-toxicodynamic modeling to predict the accumulation and toxicity of metal mixtures to zebrafish larvae [J]. Environmental Pollution, 2016, 213(2):16-29.
[63] Harder A, Escher B I, Schwarzenbach R P. Applicability and limitation of QSARs for the toxicity of electrophilic chemicals [J]. Environmental Science & Technology, 2003, 37(21): 4955-4961.
[64] Nichols J W, Bonnell M, Dimitrov S D, et al. Bioaccumulation assessment using predictive approaches [J]. Integrated Environmental Assessment and Management, 2009, 5(4): 577-597.
[65] Hendriks A J, van der Linde A, Cornelissen G, et al. The power of size. 1. Rate constants and equilibrium ratios for accumulation of organic substances related to octanol-water partition ratio and species weight [J]. Environmental Toxicology and Chemistry, 2001, 20(7): 1399-1420.
[66] Rubach M N, Ashauer R, Maund S J, et al. Toxicokinetic variation in 15 freshwater arthropod species exposed to the insecticide chlorpyrifos [J]. Environmental Toxicology and Chemistry, 2010, 29(10): 2225-2234.
[67] Buchwalter D B, Cain D J, Martin C A, et al. Aquatic insect ecophysiological traits reveal phylogenetically based differences in dissolved cadmium susceptibility [J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(24): 8321-8326.
[68] OECD. Current Approaches in the Statistical Analysis of Ecotoxicity Data: A Guidance to Application, volume 54 of Series on testing and assessment[R]. Paris, 2006.