0 引 言
以难降解有机物和重金属为代表的污染物作为现代工业的产物,对土壤及地下水的污染问题越发严重[1-2]。土壤中水分作为污染物在土壤中扩散的载体,其运动直接控制着污染物在土壤中的扩散。同时,土壤中水分运动对土壤营养物质的输送和水文气象的模拟起着极其重要的作用。虽然有关饱和土壤中水分、溶质运移规律各类参数的测定已经有了成熟的测定方法,但是以非饱和土壤水分运动为基础的污染物的运移规律仍需要进一步研究[3-5]。因而,探求、掌握非饱和土壤的水分运动规律,对预测污染物的扩散以及农业工程、水文预测都具有极重要的意义。
对于非饱和土壤中的水分运动规律的研究,国内外研究者已经形成了数学模型模拟、实验验证相结合的研究体系。实验研究中使用最多、最常见的是室内水平土柱实验,它可以消除重力作用对非饱和土壤中水分运动的影响,使影响水分运动因素更为单一,使参数的确定更为准确。研究人员关于水分运动规律的研究已经提出了多种模型[6,7]。Richards提出的非饱和土壤水分运动模型,即经典Richards模型[8],得到了广泛认可。不少研究人员对Richards模型进行了修正、简化,结合实验结果在此基础上提出了许多数学模型[9-10]。经典Richards模型对符合Boltzmann尺度律的水分运动现象具有很好模拟效果,而对广泛存在的非饱和土壤水分运动中的非Boltzmann尺度律模拟具有极大的局限性。
非饱和土壤中水分运动往往会受到土壤内部复杂的孔隙结构及复杂的边界条件影响,并且在水分运动过程中土壤内部的孔隙结构并不是固定的,因而如何准确地描述非饱和土壤中水分的运动规律具有一定的难度。已有研究表明,土壤中的颗粒分布、孔隙结构及孔隙连通性皆呈现出分形特征[11-13]。越来越多的科研工作开始借助分形工具描述复杂的土壤孔隙结构,进而利用分形工具研究非饱和土壤中水分的反常运动规律[14-16]。Chen[17]提出了分形导数的概念,构建了分形理论在非饱和土壤水分运动应用的基础,使分形工具在非饱和土壤中水分扩散的应用得以实现。Sun等[18]在此基础上提出了分形导数Richards模型,并且对满足非Boltzmann尺度律规律的非饱和土壤水分运动取得良好的模拟效果。本文从水平土柱实验出发,借助分形导数Richards理论,对不同颗粒级配非饱和土壤中水分运动进行模拟研究,探究土壤颗粒级配及其他实验条件对非Boltzmann尺度律参数的影响,验证分形导数在非饱和土壤水分运动规律研究中的有效性。
1 实验部分
1.1 实验系统
室内水平土柱实验具有操作简单、可重复性强、成本低和易于控制实验条件等优点,被广泛运用于非饱和土壤的水分运动实验中。水平土柱实验系统如图1所示,由马氏瓶、实验土柱及含水率测量装置组成。马氏瓶为实验供水装置。实验土柱为透明有机玻璃制品,有效长度为100 cm,内径为10 cm,土柱一侧距离前端40,60,80 cm处设有直径4 cm的圆孔,用以放置测量含水率的探针,土柱前端与水室相连,土柱末端底盘上均匀留有透气圆孔,以保证在实验过程中土柱土壤孔隙中的空气始终与大气压相连通,避免产生正压影响非饱和土壤中的水分运动。含水率测量装置由TDR土壤含水率测量仪及探头组成,探头上均匀布有3只探针,实验中探针插入土壤内部,测得的电信号通过导线传递到TDR土壤含水率测量仪上,转化为对应的土壤含水率读数显示在测量仪上。
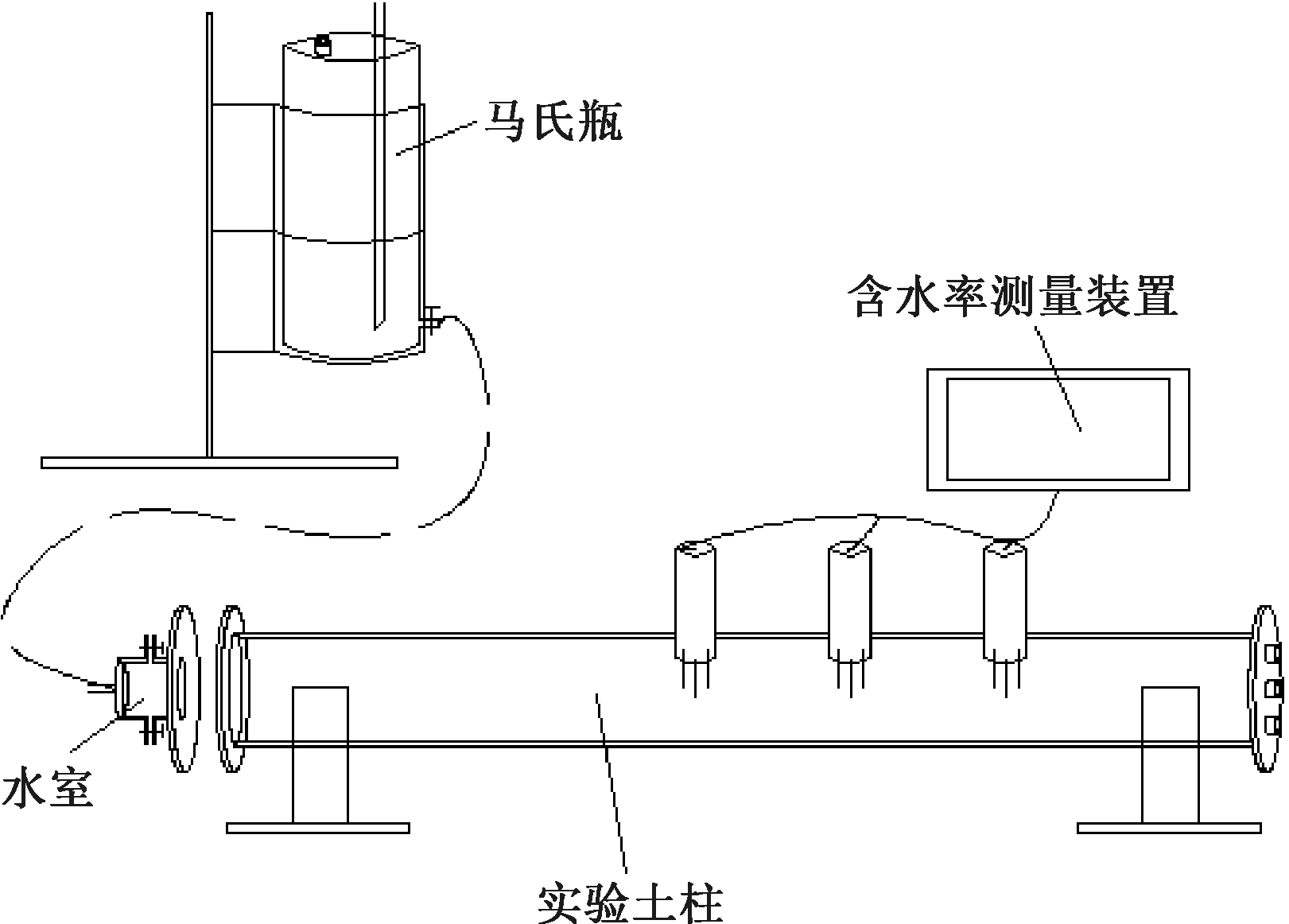
图1 含水率测量系统
Fig.1 Setup of the experiment system
1.2 实验样本与方法
实验选用4种不同组成的土样进行研究分析,分别命名为A、B、C、D,实验土样分别经直径为2.36,2.36,0.6,1.18,0.6 mm的标准筛筛分。根据实验压力不同,A组土样进行A1、A2两次实验,A1压力水头略大于A2压力水头;A、B组实验原始土样相同,标准筛筛分孔径不同;A、C、D组实验原始土样均不同。4种土样分别经直径2.36,1.18,0.6,0.3,0.15 mm的标准筛筛分进行级配的测定,土样颗粒大小的基本分布情况如表1所示。
表1 土壤颗粒样本级配
Table 1 Soil grains samples’grading %

土样级配/mm1.18~2.360.6~1.180.3~0.60.15~0.30.15A1.449.8144.2339.365.16B——49.0143.41 7.58C—5.3243.6746.40 4.60D——3.1335.37 61.51
经过筛分处理后的土样,充分混合均匀后逐层装入已固定位置土壤含水率测量探针的玻璃土柱中。每组实验中含水率测量探针的位置见表2。层间土样经压实处理,层间土样表面粗糙化处理,填满玻璃土柱中的土样整体经振捣后压实处理。将已填满被测土样的实验玻璃土柱与水室连接在一起。水平放置土柱,调节马氏瓶的出水口位置至设计高度。水室进水口与马氏瓶由橡胶软管相连。实验开始时记录马氏瓶水位初始信息,打开马氏瓶出水阀门并记录实验时间。根据不同土样实验条件确定合适的时间间隔,记录各时间间隔马氏瓶水位信息、土柱中湿润锋的位置以及所测点土壤含水率的读数。
表2 土壤含水率测量探针位置
Table 2 Measurement probe position for soil moisture
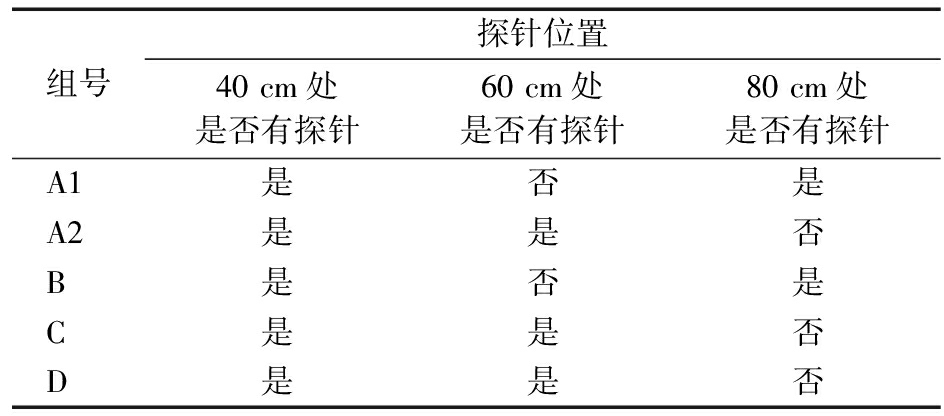
组号探针位置40 cm处是否有探针60 cm处是否有探针80 cm处是否有探针A1是否是A2是是否B是否是C是是否D是是否
2 表征方法
经典Richards模型其表述形式见式(1):
(1)
式中:θ为土壤中的含水率;D(θ)为水分在土壤中的扩散系数。有研究表明,扩散系数D是一个与运动时间和土壤含水率均有关的系数[19],在这里假设式中D(θ)为仅与土壤含水率有关的扩散系数,即仅考虑扩散系数与土壤含水率之间的关系。在一维水平土柱水分运动的模拟中,经典Richards模型是最为有效的模拟系统,在各种介质的模拟中具有十分广泛的运用。在含水率保持不变的情况下,水分运动距离X与运动时间t满足Boltzmann尺度律:水分运动距离X与运动时间t的均方根呈正相关,即X~t1/2。为了方便式(1)的求解,通过Boltzmann尺度律进行变换,引入关于θ的函数λ=X·t-1/2,可以将式(1)由偏微分方程转换为方便求解的常微分方程,在扩散系数为常数的情形下可以求得方程的解析解,具体的变换形式为:
(2)
式中:λ仅为关于θ的函数。
在非饱和土壤中水分运动室内实验或室外观测的非饱和土壤中水分运动的湿润锋运动距离与运动时间的关系中,已有研究发现其运动广泛存在反常扩散现象[10,20]。因而为满足对非饱和土壤水分反常运动规律模拟的需要,需要更具有一般意义的尺度律,即非Boltzmann尺度律:
X=λ(θ)·tα/2
(3)
式中:α∈(0,2)且α≠1。值得注意的是,当α=1时,式(3)就退化为经典的Boltzmann尺度律。已有研究发现,非饱和土壤中的水分运动满足非Boltzmann尺度律参数[18]。
Chen[17]提出了分形导数的概念,为分形工具在非饱和土壤中水分运动研究提供了方法。Sun等[18]在此基础上提出了分形Richards模型解释和刻画了非Boltzmann尺度,其方程式表示为:
(4)
式中:α为分形导数的阶数;Dα(θ)为分形Richards形式水分扩散系数,是关于含水率的函数。陈文等[21]指出,在α<1的情形下,分形Richards方程相比于经典Richards方程更能描述土壤中含水率随时间的非指数衰减规律。在非Boltzmann尺度律下,复杂的分形Richards方程可以转化为常微分方程,具体变换形式如式(5)所示:
![]()
(5)
通常认为的扩散系数Dα(θ)与含水率θ之间的关系有2种表述:幂函数形式和指数函数形式[22-23]。Sun等[18]已经就扩散系数符合含水率幂函数形式即Dα(θ)=D0θn时分形Richards方程近似解在非饱和土壤水分运动中的应用做了详细的研究并取得不错的效果。
式(4)中扩散系数Dα(θ)与含水率θ呈指数函数关系时,其解的表达式可以表达为以下形式[18,23]:
![]()
(6)
![]()
(7)
S2=D0[en(2n(-1)-n(-2))-n(-1)+n(-2)]
(8)
a=(enn(-1)-1-n(-1))/(en-1)
(9)
式中:D0为与土壤性质有关的参数;Ei为指数积分函数;S为土壤吸水率;n为与孔隙大小分布相关的参数,n>0。
本文验证在扩散系数为含水率的指数函数形式:Dα(θ)=D0enθ时,分形Richards方程对实验数据模拟的有效性以及探求不同实验条件下土壤颗粒级配对非Boltzmann尺度律参数的影响。
3 结果与分析
3.1 非Boltzmann尺度律参数的确定
在室内土柱中非饱和土壤水分运动实验中,土柱中湿润锋的位置随时间的变化对于研究水分在非饱和土壤中的运动具有至关重要的作用。记录不同时间间隔内水平土柱湿润锋的位置,借助数据分析软件分析实验数据所呈现的规律。本文中室内水平土柱实验中呈现的实验结果表现为非Boltzmann尺度律α/2>0.5的情形,详见图1。
图2为非Boltzmann尺度律曲线对实验数据的指数拟合效果图可知:使用实验数据所呈现的现象均可以使非Boltzmann尺度律进行拟合分析,拟合结果中相关系数R2均>0.99,土壤湿润锋与时间的相关性分析达到极显著水平,可以认为水平土柱水分运动实验的结果符合非Boltzmann尺度律现象。
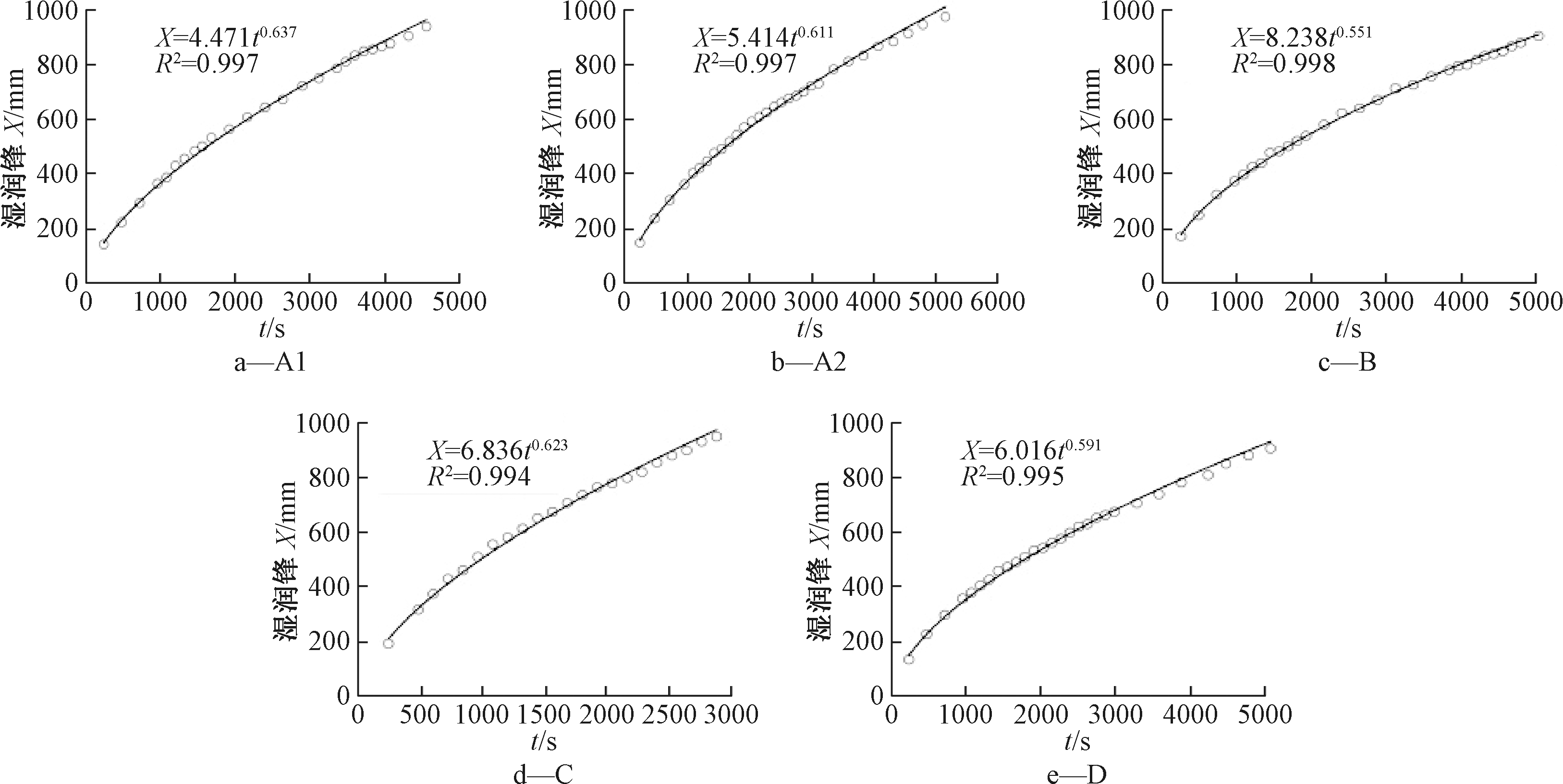
图2 不同水平土柱实验湿润锋随时间变化
Fig.2 Variation of wet front of horizontal soil column experiment with time
观察实验土壤样本的级配与非Boltzmann尺度律参数,A、B、C、D组土壤颗粒粒径分别为0.15~0.6,0.15~0.6,0.15~0.6,0.3 mm,均达到本组土壤总颗粒含量的80%以上,可以发现少量其他粒径大小的颗粒对非Boltzmann尺度律参数有显著影响。对比分析A、C、D组土壤级配与非Boltzmann尺度律参数,可以发现,随着土壤颗粒不均匀程度增加,非Boltzmann尺度律参数呈增大趋势;对比分析B、D组级配与非Boltzmann尺度律参数,可以发现在土壤主体颗粒直径(认为颗粒直径占总颗粒的80%土壤颗粒,即为主体颗粒直径)集中在某一区间范围时,大于主体颗粒直径的土壤颗粒对非Boltzmann尺度律参数的影响,高于主体颗粒直径以下的土壤颗粒对非Boltzmann尺度律参数的影响;对比分析A1、A2组实验可看出,相对于较小的实验水头,较大的实验水头会增大非Boltzmann尺度律参数。
3.2 分形Richards方程参数的确定
使用指数函数形式分形导数Richards模型分别对含水率空间分布及含水率的穿透曲线进行拟合分析,以验证模型在非饱和土壤水分运动模拟中的有效性。在参数拟合过程中,将实验数据得到的非Boltzmann尺度律参数作为分形导数Richards方程的阶数对实验含水率分布规律拟合分析。
3.2.1 含水率空间分布
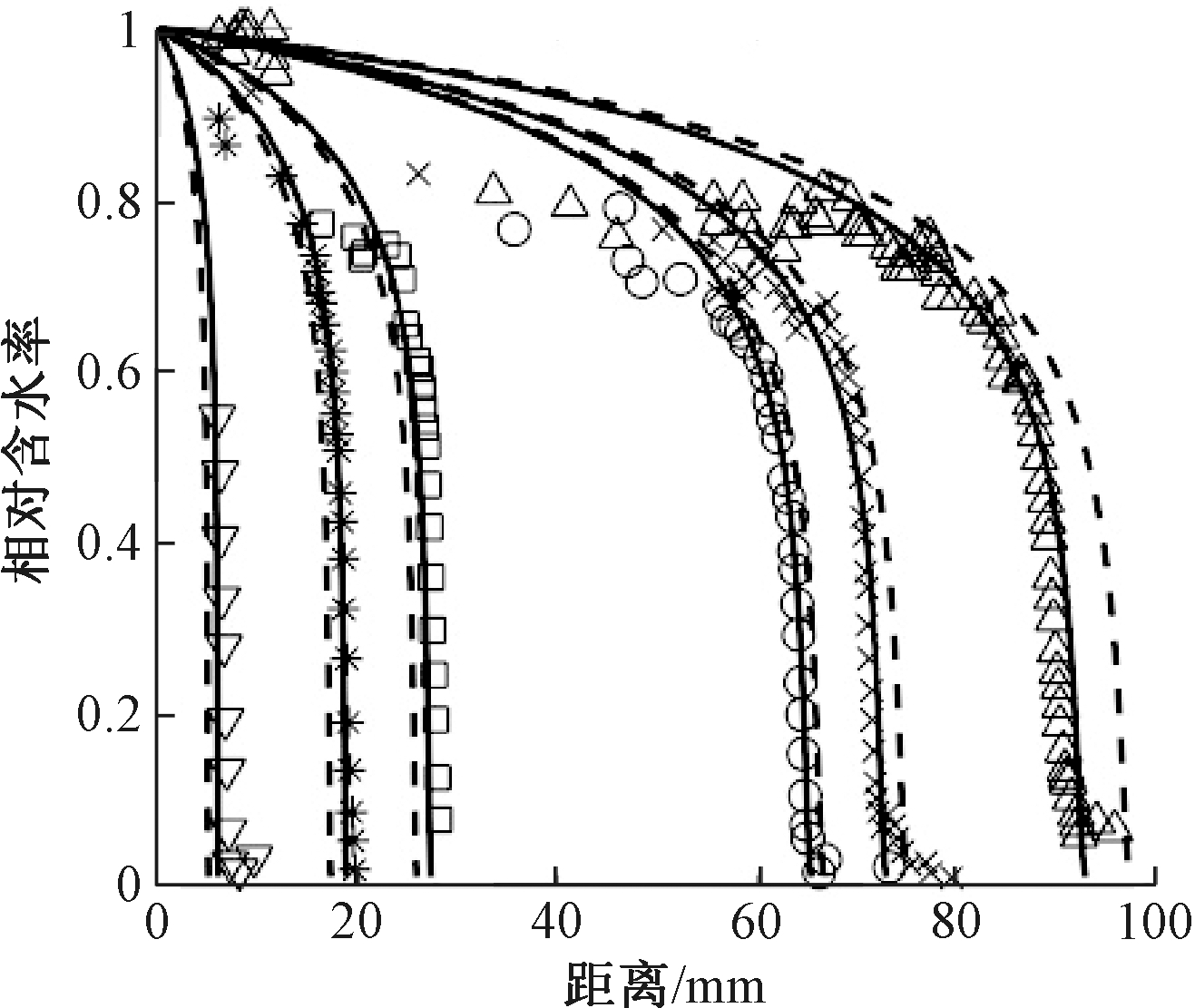
分形导数Richards计算结果与文献[24]中的实验数据拟合效果见图3。exp d1~exp d6分别为时间t=450,5370,12030,79770,101010,170330s时所得到的相对含水率,实验数据所对应的非Boltzmann尺度律参数为0.462。扩散系数为含水率指数函数时分形导数Richards的拟合参数,D0=0.000125,n=8.05。
![]() exp d1;
exp d1;![]() exp d2;
exp d2;![]() exp d3;
exp d3;![]() exp d4;
exp d4;![]() exp d5;
exp d5;![]() exp d6;——FRE;---CRE。
exp d6;——FRE;---CRE。
图3 白硅酸盐砖含水率空间分布实验结果与分形导数Richards模型计算结果
Fig.3 Experimental results of white silicate bricks’water content snapshots and calculation results by fractal Richards’models
图3中实线与虚线分别为分形导数Richards方程与经典Richards方程在扩散系数为含水率的指数函数时最佳拟合曲线。其中,分形导数Richards方程拟合曲线RMSE(均方根误差)为0.1093,经典Richards方程拟合曲线RMSE为0.2323,分形导数Richards方程在非Boltzmann尺度律参数α/2<0.5的情形下,拟合效果优于经典Richards方程拟合效果。由图3中可看出:分形导数Richards方程对于实验数据所呈现的由时间变化引起的空间分布具有很好的描述。
3.2.2 含水率穿透曲线
分形导数Richards计算结果与实验数据拟合效果见图4。图4中分形导数Richards最佳拟合参数见表3。由参数值可知:n的取值与土壤含水率的变化快慢呈正相关:n值越大,土壤含水率的变化速度越迅速;n值越小,土壤含水率的变化速度越缓慢。图4中分形Richards方程及经典Richards方程各拟合曲线的均方误差(RSME)值见表4,经典Richards模型拟合数据的RMSE为分形Richards模型的1~6倍。表明在非Boltzmann尺度律参数α/2>0.5情况下,分形导数Richards模型对实验数据的拟合结果明显优于经典Richards模型,并且可看到,分形导数Richards模型对实验数据的拟合优势随着实验中呈现的非Boltzmann尺度律参数的增加而不断扩大。
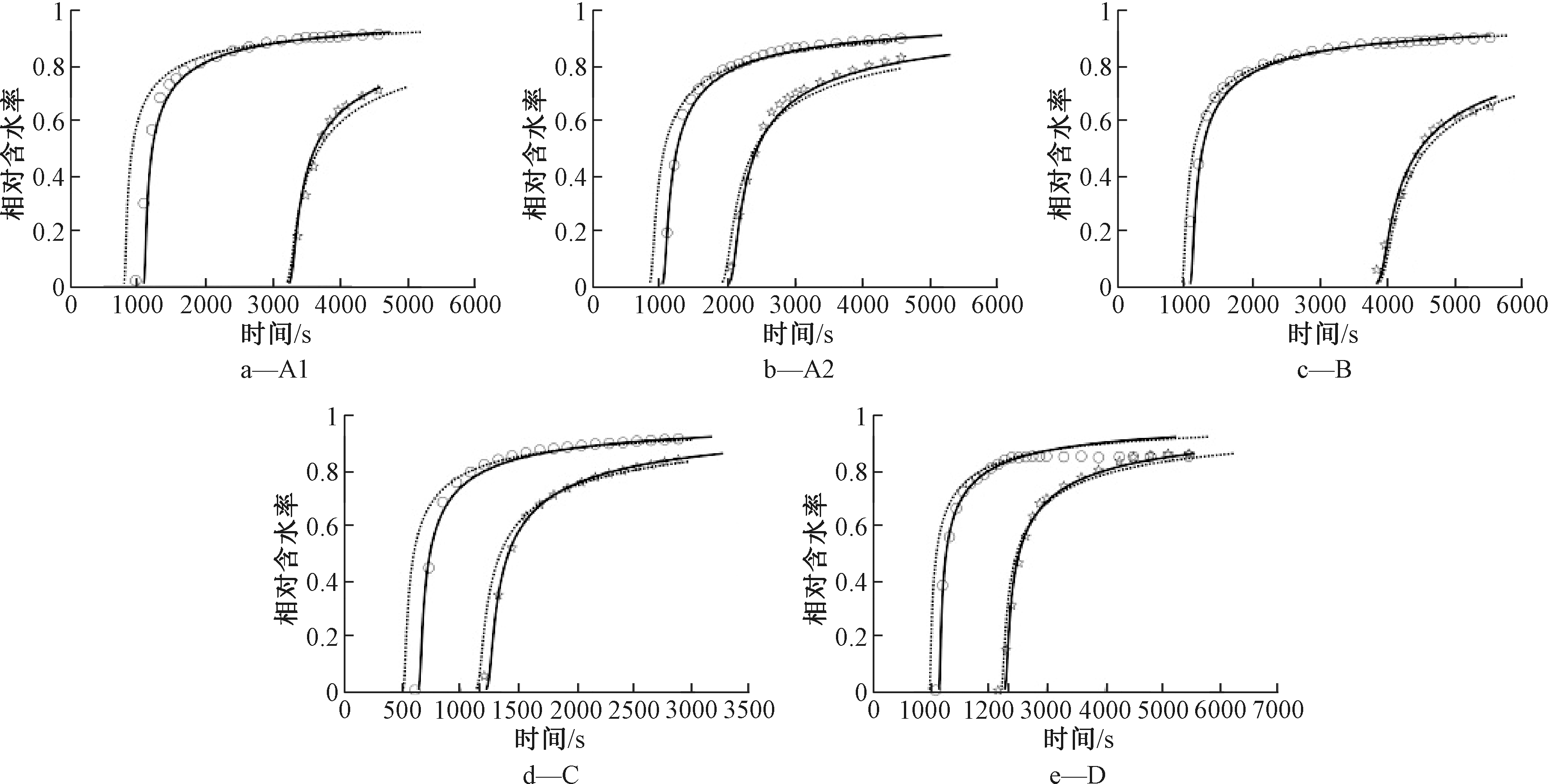
注:A1、A2、B、C、D分别为5组土柱实验中含水率穿透曲线图;实线和虚线分别为分形导数Richards及经典Richards最佳拟合曲线。![]() expd1;
expd1;![]() expd2;——FRE;……CRE。
expd2;——FRE;……CRE。
图4 含水率穿透曲线实验结果与分形导数Richards模型计算结果
Fig.4 Experimental results of water content breakthrough curves and calculation results by fractal Richards’models
表3 分形导数Richards近似解拟合参数
Table 3 Fitting parameters of fractal derivative Richards approximate solution
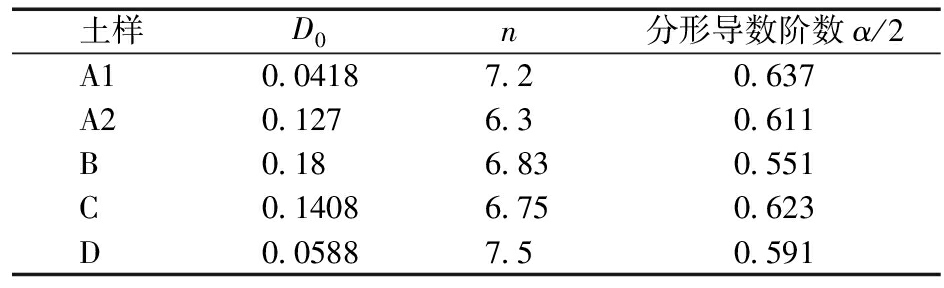
土样D0n分形导数阶数α/2A10.04187.20.637A20.1276.30.611B0.186.830.551C0.14086.750.623D0.05887.50.591
表4 拟合曲线均方根误差
Table 4 Root mean square error of the fitting curves
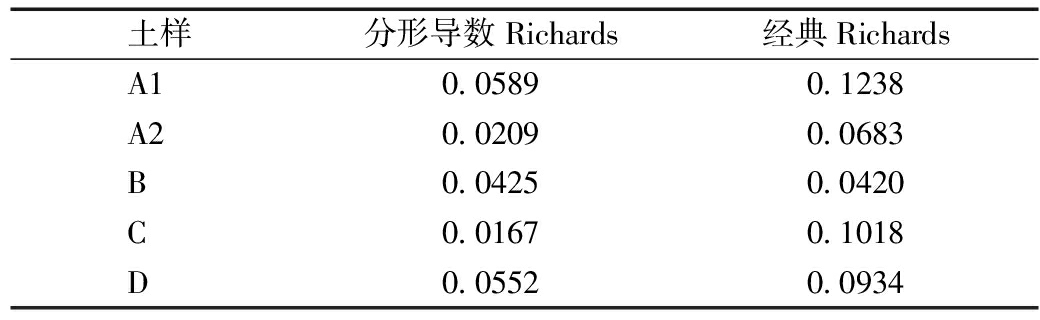
土样分形导数Richards经典RichardsA10.05890.1238A20.02090.0683B0.04250.0420C0.01670.1018D0.05520.0934
由图4中同样可看出:分形导数Richards方程准确描绘了实验数据前端及末端呈现的运动趋势,且对水分在土壤中长距离运动所得到的实验数据具有较好的拟合效果,因此可以利用这一特性对观测条件受限的区域进行水分运动的预测。
4 结 论
非饱和土壤水分运动实验满足非Boltzmann尺度律,非Boltzmann尺度律参数随土壤颗粒的不均匀程度的增加而增大,土壤中大颗粒的存在会导致非Boltzmann尺度律参数的增加,实验压力水头增加同样有利于非Boltzmann尺度律参数的增大。
分形导数Richards模型对于非饱和土壤水分运动的模拟非常有效,对非Boltzmann尺度律参数<0.5(或>0.5)的非饱和土壤水分次扩散(或超扩散)现象均具有很好的模拟效果,同时拟合结果也验证了将非Boltzmann尺度律参数作为分数导数Richards模型的阶数来模拟非饱和土壤中水分运动的方法是合理的。
在模拟中也发现:分形导数Richards方程对实验数据的模拟效果并不会随时间或空间距离的累积而减弱,因此可以利用分形导数Richards模型对非饱和土壤中的水分运动进行较为精确的预测。
[1] Arias-Estévez M, López-Periago E, Martínez-Carballo E, et al.The mobility and degradation of pesticides in soils and the pollution of groundwater resources[J].Agriculture Ecosystems & Environment, 2008, 123(4):247-260.
[2] Wuana R A, Okieimen F E.Heavy metals in contaminated soils: a review of sources, chemistry, risks and best available strategies for remediation[J].Isrn Ecology, 2011(2090/4614):1-20.
[3] Klute A, Dirksen C.Hydraulic conductivity and diffusivity: laboratory methods[M].Madison: American Society of Agronamy, 1986.
[4] Philip J R.General method of exact solution of the concentration-dependent diffusion equation[J].Australian Journal of Physics, 1960, 13(1):1.
[5] Bradford S A, Yates S R, Bettahar M, et al.Physical factors affecting the transport and fate of colloids in saturated porous media[J].Water Resources Research, 2002, 38(12):63.
[6] Bruce R R, Klute A.The measurement of soil moisture diffusivity1[J].Soil Science Society of America Journal, 1956, 20(4):458-462.
[7] Zhao R J.The Xinanjiang model applied in China[J].Journal of Hydrology, 1992, 135(1/4):371-381.
[8] Richards L A.Capillary conduction of liquids through porous mediums[J].Physics, 1931, 1(5):318-333.
[9] Wang Q J, Shao M A, Horton R.A simple method for estimating water diffusivity of unsaturated soils[J].Soil Science Society of America Journal, 2004, 68(3):713-718.
[10] Pachepsky Y, Timlin D, Rawls W.Generalized Richards’equation to simulate water transport in unsaturated soils[J].Journal of Hydrology, 2003, 272(1):3-13.
[11] Miao C Y, Wang Y F, Wei X, et al.Fractal characteristics of soil particles in surface layer of black soil[J].Chinese Journal of Applied Ecology, 2007, 18(9):1987-1993.
[12] Bartoli F, Philippy R, Doirisse M, et al.Structure and self-similarity in silty and sandy soils: the fractal approach[J].European Journal of Soil Science, 1991, 42(2):167-185.
[13] Rieu M, Sposito G.Fractal fragmentation, soil porosity, and soil water properties: I.Theory[J].Soil Science Society of America Journal, 1991, 55(5):1239-1244.
[14] 李云开, 杨培岭, 任树梅,等.土壤水分与溶质运移机制的分形理论研究进展[J].水科学进展, 2005, 16(6):892-899.
[15] Peyton R L, Gantzer C J, Anderson S H, et al.Fractal dimension to describe soil macropore structure using X ray computed tomography[J].Water Resources Research, 1994, 30(3):691-700.
[16] Xiao B, Zhang X, Wang W, et al.A fractal model for water flow through unsaturated porous rocks[J].Fractals-complex Geometry Patterns & Scaling in Nature & Society, 2018, 26(2):1840015.
[17] Chen W.Time-space fabric underlying anomalous diffusion[J].Chaos Solitons & Fractals, 2006, 28(4):923-929.
[18] Sun H G, Meerschaert M M, Zhang Y, et al.A fractal Richards’equation to capture the non-Boltzmann scaling of water transport in unsaturated media[J].Advances in Water Resources, 2013, 52(4):292-295.
[19] Guerrini I A, Swartzendruber D.Soil water diffusivity as explicity dependent on both time and water content[J].Soil Science Society of America Journal, 1992, 56(2):335-340.
[20] Küntz M, Lavallée P.Experimental evidence and theoretical analysis of anomalous diffusion during water infiltration in porous building materials[J].Journal of Physics D Applied Physics, 2001, 34(16):2547.
[21] 陈文, 梁英杰, 杨旭.基于Hausdorff分形导数Richards方程的土壤入渗率和水文模型类型[J].应用数学和力学, 2018, 39(1):77-82.
[22] Pachepsky Y, Timlin D.Water transport in soils as in fractal media[J].Journal of Hydrology, 1998, 204(1):98-107.
[23] Parlance M B, Prasad S N, Parlange J Y, et al.Extension of the Heaslet-Alksne technique to arbitrary soil water diffusivities[J].Water Resources Research, 1992, 28(10):2793-2797.
[24] Ridgway C J, Gane P A C, Abd E G E, et al.Water absorption into construction materials: comparison of neutron radiography data with network absorption models[J].Transport in Porous Media, 2006, 63(3):503-525.