0 引 言
随着人口持续增长和城市化进程不断加深，城市空气污染越来越严重，影响范围也越来越广。空气污染物的来源也发生了变化，由工业废弃物、焦煤排放的NOx和SO2等传统污染物，转变为悬浮在空气中的细微颗粒物(PM，主要由机动车排放、空气扬尘等产生)[1-3]。GB 3095—2012《环境空气质量标准》使用空气质量指数(air quality index，AQI)来评估当日的空气质量，将PM2.5(细颗粒物，直径≤2.5 μm)、PM10(细颗粒物，直径≤10 μm)、SO2、CO、NO2和O3 6种污染物指标纳入AQI的计算公式中，更科学、更全面地体现了空气中不同污染源对空气质量的影响。
为了探索空气污染指标时间序列的动力特征，近年来，国内外学者从不同的视角探索了城市AQI及其污染物的形成规律，如污染物的时空特征[4，5]、来源分析[6]、气象因素[7，8]、社会经济因素对空气质量的影响[9]等。少数学者研究了AQI和污染物之间的关系：戴孟莲等[10]使用偏相关和逐步回归方法分析AQI与6种污染物指标的相关性；陈优良等[11]研究得出环鄱阳湖城市群PM2.5与O3呈正相关；罗岳平等[12]在研究长沙、株洲和湘潭(以下简称长株潭)城市环境空气时发现PM2.5与O3呈负相关，不产生叠加污染；刘艳萍等[13]在研究城市群(长三角、珠三角、京津唐、辽中南)时，通过比较PM2.5与PM10、SO2、CO、NO2及O3的相关系数，发现有些城市群PM2.5的浓度与PM10、SO2、NO2、CO的浓度呈显著正相关，认为这5种污染物具有一定的同源性，而PM2.5与O3相关性不明确；李婷婷等[14]分析了中三角城市群整体空气质量特征及变化趋势。然而，上述研究仅限于同区域各种污染物之间，未涉及城市群内部各城市间空气污染的相互影响效应。
由于空气的流动性，某地区的污染会不同程度地影响其周边城市，因此，相邻地区的空气质量指标会出现“联动效应”，而关于这方面的研究较少。Liu等[15]认为，邻近城市的PM2.5序列不仅存在很强的关联，而且还存在明显的时间滞后；Gong等[16]发现，城市空气污染存在明显的空间溢出效应；Shen等[17]发现，我国典型城市群的PM2.5浓度呈显著的空间聚类特征；Jiang等[18]从计量经济学的角度，检验北京与周边城市空气污染之间的因果关系，发现保定至北京之间存在单向关系，京津之间存在双向关系。王访等[19-21]利用多重分形理论探索了长株潭和京津冀地区两两城市间PM2.5序列存在相关性，发现不同城市在不同季节和不同时间尺度上对其他城市有不同影响，为探寻影响相邻城市空气质量的污染源提供了新的视角。
受多种因素影响，污染物序列的动力结构表现为多种非线性特征并存。因此要更准确地揭露其统计规律和动力学特征需要新型的统计手段。近几十年，学者们就非线性时间序列分析的理论方法和应用方面进行了大量的研究，提出了很多实用的方法。熵作为一种通过量化不确定性程度来检测时间序列复杂性的方法，在各个领域得到了广泛的应用。例如，Pincus[22-24]提出的近似熵(approximate entropy，AE)用于研究生物时间序列；Richman等[25]提出样本熵(sample entropy，SE)，用于研究心血管等生理时间序列；刘慧等[26]认为样本熵比近似熵更具相对一致性，更符合理论性； Liu等[27]发展了交叉样本熵(cross-sample entropy，CSE)，用于研究外汇时间序列；Costa 等[28]介绍了1种计算复杂时间序列多尺度熵的方法(multi scale entropy，MSE)，用于复杂生理时间序列分析。最近，Wu等[29]引入了基于符号表示和相似性的改进的多尺度交叉样本熵测度(multiscale cross-sample entropy measure based on symbolic representation and similarity，MCSEBSS)，用于研究中美两国股市的相似度，但这种方法对于具有趋势的时间序列的处理太粗糙，难以真实反映趋势对不一致性的影响。
对于趋势的考虑，Peng等[30]提出去趋势波动分析(detrended fractal analysis，DFA)，并应用于DNA序列分析，解释了其具有独特的自相似结构[31]，这个方法为研究时间序列中遭遇的非平稳性和强趋势性开辟了一条新思路。Kantelhardt等[32]将DFA推广到多重分形版本(multifractal DFA)。Podobnik等[33,34]，基于DFA，提出了去趋势互相关分析(detrended cross-correlation analysis，DCCA)和多重分形去趋势互相关分析(MF-DCCA)，用于处理2个非平稳序列互相关问题。作为在空气质量相关序列的应用研究：Xu等[35]利用MF-DCCA分析了NO、NO2和O3之间的相互关系；Manimaran等[36]运用MF-DCCA分析了空气污染指数序列的多重分析特征及9种污染因子间的互相关关系。还有学者将熵思想与多重分形方法相结合，研究了序列的趋势对长程相关性的影响[37]。
针对MCSEBSS在处理趋势序列中的缺陷，借用MF-DFA中去趋势的思想，本文提出了1种新的多尺度交叉趋势样本熵(multiscale cross trend sample entropy，MCTSE)，能有效刻画2个非平稳序列在不同尺度上的相似性，并利用该方法研究了相邻城市AQI与6个空气污染指标的一致性。一方面，深度探寻了影响每个城市不同季节不同时间尺度上AQI的污染因子的种类与强度；另一方面，考虑了AQI及每种污染物在两两相邻城市间的相似度，从而筛选出两两城市间最相似的且污染最严重的污染物，为相邻城市共同治理空气污染提供参考。
1 方法与数据来源
1.1 多尺度交叉趋势样本熵(MCTSE)
设长度为N的时间序列x={x(i),i=1,2,…,N}和y={y(i),i=1,2,…,N}。在时间尺度t下(本文取时间尺度t为4～20，步长为1)，用粗粒化过程构造连续粗粒序列xt={xt(j),j=1,2,…,p}，yt={yt(j),j=1,2,…,p},其中p=[N/t]，得到的粗粒序列{xt}和{yt}即为在分割的小区间内的平均值序列。
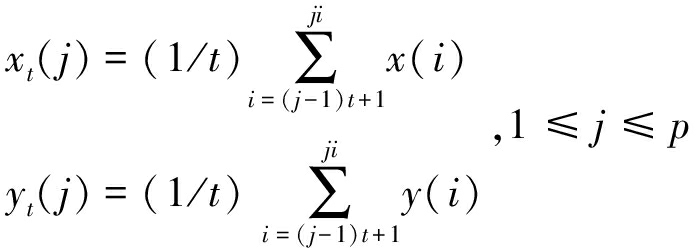
(1)
然后用符号序列{Xt(j)}和{Yt(j)}来表示粗粒序列xt和yt。利用多项式(线性、二次或高阶等)拟合得到其趋势
和
符号序列{Xt(j)}和{Yt(j)}定义为:
(2)
上述符号序列{Xt(j)}和{Yt(j)}体现了2个原始序列去除趋势后的动力特征，对于非平稳时间序列是十分重要的步骤。而在Wu等[29]提出的MCSEBSS中，符号化序列通过比较粗粒序列与其均值的大小关系获得，未考虑趋势对原始序列的影响。
接着，从得到的符号序列Xt和Yt中分别构造模板向量
和
其中m为滑动窗口的长度。
0≤k≤m-1,1≤i<p-m.
(3)
进一步根据Kronecker函数，定义布尔变量f为两模板向量和
之间的符号函数，如式(4)所示，进一步得到长度为m的符号向量
(4)
定义
来表征计算
和
之间的一致性。
1≤i≤p-m
(5)
其后进行模板匹配，类似于MCSEBSS，当比超过r时，m维模板向量匹配数标记为
例如,对于
通过比较与r，计算得到模板匹配的数量为
然后依次对于
计算得到其模板匹配数分别记为
则m维模板向量的总数可由
表示。
最后，修改m为m+1，重复上述步骤，便可得到m+1维模板向量的总数量。所以，基于MCTSE的熵值为：
(6)
注意，参数r的选择在计算熵值时至关重要，根据文献[29]，设置参数
本文在计算r时，采用m=2，n=1。值得说明的是,MCTSE区别于其他交叉样本熵方法的关键步骤是式(2)，在式(2)中，粗粒序列的趋势通过多项式拟合(考虑分季节讨论各序列，本文采用一次多项式拟合趋势)，其优点在于多项式可将包括正弦趋势在内的大多数趋势去除，能有效处理具有强烈趋势的非平稳序列。
1.2 数据来源
湖南省中东部的长沙、株洲、湘潭(两两城区分别距离约为48,45,25 km)3个城市呈“品”字形，分布于罗霄山脉与雪峰山脉之间的湘江河谷平原区，呈现南高北低地形，属于亚热带季风性气候，气流交汇，大气污染相互叠加，导致区域性的空气污染。近年来，3个城市经济飞速发展，呈现经济联动效应，同时也形成区域性污染特征，因此，本文选取3个城市的AQI和各污染指标(PM2.5、PM10、SO2、CO、NO2及O3)的日均数据为研究对象，数据来源于天气后报网(http://www.tianqihoubao.com/aqi/)，数据采集窗口为2013-12-01—2017-11-30(共计1461个观察样本)。其中，长沙、株洲和湘潭各有3天的数据缺失，缺失的数据用线性插值方式填补。AQI及6种污染物指标的时间序列如图1所示。可知：3个城市的AQI时间序列以及3个城市每种污染物时间序列的趋势大体一致，这表明存在着潜在的关联性。此外，AQI及每种污染物具有明显的季节效应，因此，将上述数据分别进行讨论，分别为冬(12月—次年2月)、春(3—5月)、夏(6—8月)、秋(9—11月)，4年间冬季共有361 d、春季有368 d、夏季有368 d、秋季有364 d。3个城市中度污染以上(AQI>150)的天数分别为：长沙，冬季109 d，春季13 d，夏季3 d，秋季23 d；株洲，冬季108 d，春季10 d，夏季2 d，秋季10 d；湘潭，冬季94 d，春季9 d，夏季4 d，秋季17 d，可见3个城市的空气质量均表现为冬季最差，夏季最佳。为了考察上述3个城市4个季节的空气质量状况的差异，表1为每个城市AQI的基本统计量，表2为每个城市AQI在4个季节的方差分析结果(给定显著性水平为1%)。由表1可知：3个城市的空气污染情况大体相似；从变异系数可知，3个城市春季AQI离散程度最小，秋季作为空气质量由好变坏的过渡期，其变化最为剧烈；表2表明3个城市的空气质量在4个季节中除春、秋两季无显著差异外，其余季节间都存在显著差异。
图1 长沙、株洲和湘潭2013—2017年AQI及6种污染物日均浓度的时间序列
Figure 1 The time series diagram of daily average values of AQI and six pollutants concentration in Changsha, Zhuzhou and Xiangtan in 2013—2017
表1 长沙、株洲、湘潭4个季节的AQI序列基本统计量
Table 1 The basic statistics of AQI series of Changsha, Zhuzhou and Xiangtan in four seasons
项目长沙株洲湘潭冬季春季夏季秋季冬季春季夏季秋季冬季春季夏季秋季均值124.9577.6460.3182.43127.0575.3453.9674.60120.4875.6959.2180.88标准差60.4330.8427.3443.2360.3229.8023.5832.3755.8526.9326.1238.90最大值356230306301356254163313361189299261最小值192417141822191725272513变异系数0.480.400.450.520.470.400.440.430.460.360.440.48
表2 长沙、株洲、湘潭的AQI在两两季节的方差分析
Table 2 Analysis of variance of AQI between each two seasons for Changsha, Zhuzhou and Xiangtan
项目四季冬vs.春冬vs.夏冬vs.秋春vs.夏春vs.秋夏vs.秋长沙F统计量149.41178.2019338.7187116.781358.45753.615666.5918 p值0.00000.00000.00000.00000.00000.0576 N0.0000株洲F统计量225.52215.4602453.7780207.2065106.23770.000995.2683 p值0.00000.00000.00000.00000.00000.9762 N0.0000湘潭F统计量161.54193.0320355.9475122.185364.016465.214676.6963 p值0.00000.00000.00000.00000.00000.0227N0.0000
注：N表示在1%显著性水平下AQI差异不显著。
2 分析与讨论
由图1和表1、2可看出：对于长沙、株洲和湘潭3个城市，各自的AQI与6种污染物时间序列的趋势在不同季节存在差异，而且传统空气污染指标(如SO2、NO2)与新型污染指标(如PM2.5、O3)时间序列也存在不同程度的差别。此外，上述3个城市之间的各种空气污染指标时间序列在不同季节也表现出不同的相关性。鉴于此，利用第1节提出的MCTSE对上述两方面进行研究：一方面，每个城市在4个季节的空气污染物与AQI的一致性；另一方面，两两城市之间的空气污染物指标的相似度。
2.1 每个城市空气污染物与AQI的一致性
运用MCTSE研究长沙、株洲和湘潭3个城市的AQI序列与6种污染物序列间的交叉趋势样本熵，结果如图2所示。
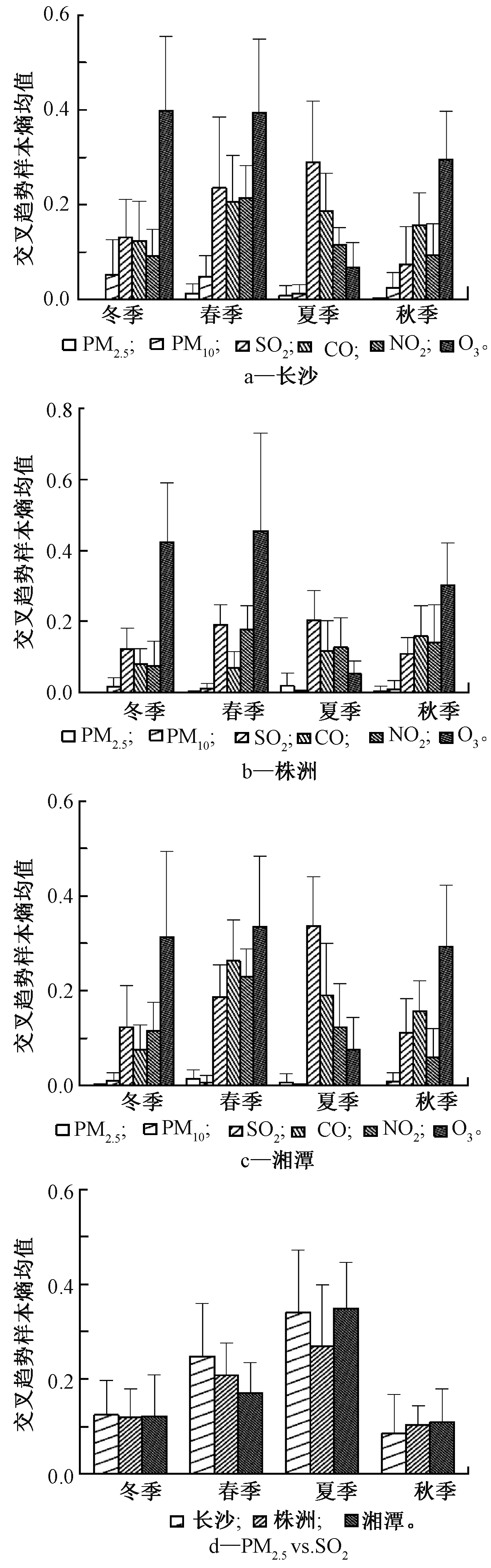
图2 长沙、株洲、湘潭4个季节的AQI指数与6种污染物的
交叉趋势样本熵的平均值及3个城市PM2.5
与SO2的去交叉趋势样本熵的平均值
Figure 2 The average of MCTSE values between AQI and six
pollutants in four seasons, and the average value of MCTSE between
PM2.5 and SO2 in four seasons in Changsha, Zhuzhou, Xiangtan
图2a—c分别为长沙、株洲和湘潭4个季度的AQI与6种污染物的交叉趋势样本熵的平均值。为了考察GB 3095—2012中组成AQI的新指标序列与GB 3095—1996《环境空气质量标准》中构成API的指标之间的一致性，选取新指标中的PM2.5指数和旧指标中的SO2浓度序列，并运用MCTSE分别对上述3个城市的四季进行了研究，其平均交叉趋势样本熵如图2d所示。
根据交叉熵的定义，2个序列的交叉熵值越低，其一致性越高。AQI与某种污染物的交叉熵值越低，表明AQI与该污染物的一致性越高，即该污染物对AQI的影响越大。由图2可看出：
1)4个季节中长沙、湘潭和株洲3个城市的PM2.5与AQI序列的交叉样本熵平均值几乎为0，即PM2.5与AQI序列高度一致，说明PM2.5在全年都是影响3个城市的首要污染物，尤其在冬季最为显著。PM10与AQI的一致性仅次于PM2.5，说明细微颗粒物污染是3个城市最主要的空气污染源之一。此外，相比其他5种污染物，3个城市4个季节的PM2.5和PM10与AQI的熵值标准差都是最小的，表明在不同时间窗口内，这2种污染物与AQI的一致度几乎没有差异。
2)O3序列只在夏季与AQI序列的平均交叉熵较低，在冬、春、秋三季与AQI的平均交叉样本熵显著较高。这是由于O3主要依赖于高温、强光照环境条件，季节变化显著。在冬季，PM2.5浓度过高引起的屏蔽、散射等作用会降低O3质量浓度；在夏季，人为排放的NOx等前体物在高温光照条件下导致近地面二次O3生成较多[11]，且PM2.5质量浓度高时会在空中为二次O3的生成提供反应表面[13]，所以夏季O3污染严重。此外，除夏季外，3个城市的O3与AQI的熵值标准差也最大，表明春、秋、冬季3个城市在不同时间窗口内的O3与AQI的一致度存在较大差异。
3)图2a显示传统污染物SO2、NO2与AQI的平均交叉样本熵值明显高于PM2.5、PM10与AQI的交叉熵，表明近几年来这3个城市的空气污染源已发生了改变，由传统的工业废弃、焦煤排放的气体污染向空气中悬浮的细微颗粒物污染转变。
4)从整体看，除了O3外，各污染物与AQI的平均交叉样本熵呈现季节性变化，秋冬季低于春夏季。这是由于3个城市均属于亚热带季风性湿润气候，夏季高温多雨，且空气对流频繁，扩散条件比较好。而冬季，空气对流差，不利于风和降水形成，污染物积聚不易扩散，且采暖燃煤量增大加大了细微颗粒物的排放，导致颗粒物占空气污染成分的比重最大(与AQI一致性最强)。
5)图2d表明PM2.5与SO2之间的相似程度呈现季节效应，秋冬两季的相似性高于春夏两季，说明在秋冬两季PM2.5与SO2具有一定的同源性[11]。而在春夏两季，二者相似性较小(熵值较大)，说明在空气质量较好的季节，PM2.5与SO2的变化趋势差异较大。
6)由图2a—c可知：3个城市的污染物变化与AQI的变化趋势大体一致，冬季污染严重，而夏季空气质量较好，因此，有必要对两两城市之间空气质量的相似性做分析。
2.2 城市间空气污染物指标的相似性
运用MCTSE分别研究长沙与株洲、长沙与湘潭，株洲与湘潭4个季节AQI和6种指标序列的交叉趋势样本熵，其交叉趋势样本熵分别如图3所示。图3a—c中由上至下分别为两两城市之间的AQI、4种传统污染指标(PM10、SO2、NO2和CO)及GB 3095—2012中新加入的PM2.5和O3的交叉趋势样本熵随时间尺度的变化。可知：
—AQI; 
—PM10; 
—SO2; 
—NO2; 
—CO; 
—PM2.5; 
—O3。
图3 长沙与株洲、长沙与湘潭、株洲与湘潭4个季节的AQI及6种污染物的多尺度交叉趋势样本熵
Figure 3 The multiscale cross trend entropy of AQI and six pollutants in four quarters between each two cities in three
1)3个城市的AQI变化趋势十分相似(4个季节的熵值均<0.1)，这是由于3个城市的地理特征及气候类型基本相同，且城市化进程(便利的交通、自由的经济活动、宽松的贸易政策等)使得3个城市已融于一体，三者间的空气质量具有联动效应。
2)两两城市间PM2.5、PM10和O3的相似度(熵值大部分<0.1)显著高于其他污染物，表明3个城市的空气污染都主要来源于空气中的细微颗粒(如煤燃烧产生的灰粒、汽车尾气、城市扬尘和建筑水泥尘等)。
3)两两城市间其他污染物的相似度呈现出冬、秋季强于春、夏季的变化趋势。其中，CO和SO2的相似度较低(熵值较大)，表明3个城市的汽车尾气量及工业排放量略有差异。
4)长沙与株洲，在夏季，6种污染物中不一致性最小为SO2，最大交叉趋势样本熵值对应为17 d；而春季最大交叉趋势样本熵值对应为12 d;长沙与湘潭，在夏季，不一致性最大的是CO，对应最大尺度为19 d;而春季转变为SO2，对应最大尺度为12 d；这是工业排放源及排放量不一致所致。株洲与湘潭，在夏季，不一致性最大亦是CO，对应最大尺度为19 d；而春季，不一致性最大为SO2，对应最大尺度为9 d；其余空气污染物的相似度都较高。
3 空气污染防治目标及防治策略建议
根据AQI与污染物浓度的交叉趋势样本熵来评估该污染物对空气质量的影响；根据城市间某污染物指标的相似度来决策是否共同防治该污染物。若某污染物与AQI的交叉趋势样本熵的平均值较大，则该污染物对空气污染的作用不明显，例如，3组城市间O3在全年的相似度都很高，但由于每个城市的O3只在夏季对空气污染影响较大，因此未考虑在其他季节对O3的控制。当两城市间的某种污染物的相似度较低时，但其中一个城市的该种污染物与AQI的一致性又较高时，该城市应制定适合本城市实情的防治空气污染的治理办法。
根据长沙、株洲及湘潭的各污染物与AQI的一致性，以及其两两城市间每个指标的相似性，在不同季节的主要空气污染防治目标如下：
1)全年长沙、株洲及湘潭都应共同防治细微颗粒物污染(汽车尾气、工业扬尘、燃气产生的烟尘等)。2)在冬季，株洲与湘潭共同防治CO(工业排放、采暖锅炉、燃放烟花爆竹和吸烟等燃料不充分燃烧)，长沙与株洲共同防治NO2(矿物燃烧和含氮燃料燃烧)。3)在春季，株洲与长沙共同防治CO；在夏季，3个城市共同防治O3(控制前体物NOx和VOCs，NOx来源于燃料燃烧及汽车尾气，而VOCs来源于汽车尾气、汽油挥发、涂料、工业排放等)；在秋季，长沙与湘潭共同防治NO2。4)长沙的秋季SO2对空气污染也有一定影响，根据PM2.5与SO2具有一定同源性，且PM2.5对AQI的影响大于SO2，因此在控制PM2.5的同时，SO2也将得到相应的控制。
在空气污染的防治策略上，加强城市内部污染源治理，要精细化管理空气污染，根据城市内部特有的污染物有针对性地制定本城市大气污染防治策略，积极开展“一市一策”研究[38]；还要联合周边城市和地区，统筹资源，实施循序渐进的跨区域合作治理政策[39]，共同治理环境污染问题。
4 结 论
本文提出了一种表征2个时间序列之间一致度的方法——MCTSE，该方法能刻画具有强烈趋势的非平稳时间序列的动力特征，并运用该方法研究了长沙、株洲及湘潭4个季节的AQI与PM2.5、PM10、SO2、NO2、CO和O3 6种空气污染物浓度的一致性及两两城市间空气污染物的相似性，结果表明：上述3个城市4个季节内均为PM2.5与AQI序列的一致性最大，说明PM2.5在全年都是影响空气质量的首要污染物，在冬季最为显著。PM10与AQI的一致性仅次于PM2.5，说明细微颗粒物污染已经取代了传统的工业废弃、焦煤排放的气体污染，成为3个城市最主要的空气污染源。相邻城市间的AQI变化趋势基本一致，表明其空气质量具有联动效应。PM2.5、PM10和O3的相似性明显高于其他污染物，而且这些污染物的相似度呈现出冬、秋季强于春、夏季的变化趋势。以上结论可为长株潭共同治理空气污染提供了合理化建议，为研究影响城市空气质量的主要污染物及相邻城市间空气污染的联动效应提供参考。
[1] 佘倩楠, 徐茜, 周陶冶,等. 长三角地区2015年大气重污染特征及其影响因素[J]. 环境科学学报, 2018, 38(8): 3185-3196.
[2] 李琛, 刘瑾, 王彦民. 气压对西安市城区空气质量的影响[J]. 环境工程, 2017, 35(3): 101-105，122.
[3] 别同, 韩立建, 何亮,等. 城市空气污染对周边区域空气质量的影响[J]. 生态学报, 2018, 38(12): 4268-4275.
[4] XU L Z, BATTERMAN S, CHEN F, et al. Spatiotemporal characteristics of PM2.5, and PM10, at urban and corresponding background sites in 23 cities in China[J]. Science of the Total Environment, 2017, 599/600:2074-2084.
[5] XIAO K, WANG Y K, WU G, et al. Spatiotemporal characteristics of air pollutants (PM10, PM2.5, SO2, NO2, O3, and CO) in the inland basin city of Chengdu, Southwest China [J]. Atmosphere, 2018, 9(2):74.
[6] 李礼, 许丽萍, 余家燕，等. 重庆主城区近年一次典型空气重污染过程分析[J]. 环境工程学报, 2017, 11(12): 6379-6385.
[7] 杨志文, 元洁, 吴琳,等. 夏季空气污染物指数与气象参数相关性分析[J]. 环境工程, 2018, 36(8): 83-87.
[8] CHAN Z Y, XIE X M, CAI J, et al. Understanding meteorological influences on PM2.5 concentrations across China: a temporal and spatial perspective [J]. Atmospheric Chemistry and Physics Discussions, 2017:1-30.
[9] HAN L J, ZHOU W Q, LI W F. Increasing impact of urban fine particles (PM2.5) on areas surrounding Chinese cities [J]. Scientific Reports, 2015, 5: 12467.
[10] 戴孟莲, 王彤, 邓海银, 等. 基于偏相关与逐步回归方法的AQI影响因素分析及预测[J]. 环境保护前沿, 2017, 7(3): 191-201.
[11] 陈优良, 陶天慧, 刘新意. 环鄱阳湖城市群空气质量时空分布[J]. 环境污染与防治, 2018, 40(12): 1418-1424.
[12] 罗岳平, 刘孟佳, 甘杰,等. 长株潭城市环境空气中PM2.5和O3质量浓度的相关性研究[J]. 安全与环境学报, 2015, 15(4): 313-317.
[13] 刘艳萍, 王明仕, 桂晨露,等. 中国工业基地城市群PM2.5时空分布特征及相关性分析[J]. 科学技术与工程, 2018, 18(15): 184-189.
[14] 李婷婷，尉鹏，程水源,等. 2005—2014年中三角城市群大气污染特征及变化趋势[J]. 环境工程学报, 2017, 11(5): 2977-2984.
[15] LIU J Z, LI W F, WU J S, et al. Visualizing the intercity correlation of PM2.5 time series in the Beijing-Tianjin-Hebei region using ground-based air quality monitoring data [J]. Plos One, 2018, 13(2): e0192614.
[16] GONG Z Z, ZHANG X P. Assessment of urban air pollution and spatial spillover effects in China: cases of 113 key environmental protection cities [J]. Journal of Resources and Ecology, 2017, 8(6): 584-594.
[17] SHEN Y, ZHANG L P, FANG X, et al. Spatiotemporal patterns of recent PM2.5 concentrations over typical urban agglomerations in China [J]. Science of the Total Environment, 2019, 655(3): 13-26.
[18] JIANG L, BAI L. Spatio-temporal characteristics of urban air pollutions and their causal relationships: evidence from Beijing and its neighboring cities [J]. Scientific Reports, 2018, 8(1):1279.
[19] 王访, 范毅.基于AMF-HXA的长株潭空气质量指数互相关性分析[J]. 环境保护前沿, 2017, 7(6): 443-452.
[20] WANG F, WANG L, CHEN Y M. Detecting PM2.5’s correlations between neighboring cities using a time-lagged cross-correlation coefficient [J]. Scientific Reports, 2017,7:10109.
[21] WANG F, WANG L, CHEN Y. A DFA-based bivariate regression model for estimating the dependence of PM2.5 among neighbouring cities [J].Scientific Reports, 2018,8(1):7475.
[22] PINCUS S M. Approximate entropy as a measure of system complexity [J]. PNAS,1991,88(6):2297-2301.
[23] PINCUS S M. Approximate entropy (ApEn) as a complexity measure [J]. Chaos， 1995,5(1):110-117.
[24] PINCUS S M. Quantifying complexity and regularity of neurobiological systems [J]. Methods in Neurosciences, 1995, 28:336-363.
[25] RICHMAN J S, RANDALL M J. Physiological time-series analysis, using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6):2039-2049.
[26] 刘慧, 和卫星, 陈晓平. 生物时间序列的近似熵和样本熵方法比较[J]. 仪器仪表学报, 2004, 25(增刊): 806-807，812.
[27] LIU L Z, QIAN X Y, LU H Y. Cross-sample entropy of foreign exchange time series [J]. Physica A：Statistical Mechanics and Its Applications, 2010, 389(21):4785-4792.
[28] COSTA M, GOLDBERGER A L, PENG C K. Multiscale entropy analysis of complex physiologic time series [J]. Physical Review Letters, 2007, 89(6):705-708.
[29] WU Y, SHANG P J, LI Y L. Multiscale sample entropy and cross-sample entropy based on symbolic representation and similarity of stock markets [J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 56:49-61.
[30] PENG C K, BULDYREV S V, HAVLIN S, et al. Mosaic organization of DNA nucleotides [J]. Journal of Physical Review. E, 1994, 49(2):1685-1689.
[31] PENG C K, HAVLIN S, STANLEY H E, et al. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series [J]. Chaos, 1995, 5(1): 82-87.
[32] KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELNY-BUNDE E, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A, 2002, 316(1/2/3/4):87-114.
[33] PODOBNIK B, STANLEY H E. Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series [J]. Physical Review Letters, 2008, 100(8): 084102.
[34] ZHOU W X. Multifractal detrended cross-correlation analysis for two nonstationary signals[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2008, 77(2):066211.
[35] XU W J, LIU C Q, SHI K, et al. Multifractal detrended cross-correlation analysis on NO, NO2 and O3 concentrations at traffic sites [J]. Physica A：Statistical Mechanics and Its Applications, 2018, 502: 605-612.
[36] MANIMARAN P, NARAYANA A C. Multifractal detrended cross-correlation analysis on air pollutants of University of Hyderabad Campus, India[J]. Physica A：Statistical Mechanics and Its Applications, 2018, 502:228-235.
[37] XIONG H, SHANG P. Weighted multifractal cross-correlation analysis based on Shannon entropy[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1/2/3): 268-283.
[38] 燕丽, 杜小申. 典型城市空气污染特征对比分析[J].中国环境管理, 2018, 10(6): 92-98.
[39] 汪伟全. 空气污染的跨域合作治理研究:以北京地区为例[J]. 公共管理学报, 2014, 11(1): 55-64，140.