0 引 言
随着我国工业高速发展,化石燃料快速消耗,大量空气污染物产生并排放到大气中,致使我国大气污染问题越发严重。空气中的悬浮颗粒物(particulate matter, PM)是空气质量的一个重要评价指标, 其中直径≤10 μm的颗粒物(PM10)是我国北方大部分城市的首要大气污染物,其不仅危害人体健康[1],且影响空气能见度。因此,及时、准确地预测PM10浓度有利于提前做好防备工作并予以控制。目前,对PM10浓度的预测方法多采用一元线性回归法[2]、多元线性回归法[3]、支持向量机法[4,5]等。随着人工智能的发展,人工神经网络(ANN)在PM10浓度预测方面取得了良好的性能[6]。然而,人工神经网络存在结构设计困难、容易收敛到局部最优和不适合小样本等缺点,严重影响预测精度。近年来,深度学习作为一种机器学习领域一个新的研究方向,在不同应用领域取得了明显的优势。深度学习模型拥有多个非线性映射层级,可以通过逐层学习掌握海量数据中蕴含的深层次的潜在规律[7]。在众多深度学习模型中,循环神经网络(recurrent neural network,RNN) 引入了时间步长的概念,在时序数据的分析中表现出更强的适应性。长短期记忆神经网络(LSTM)改进了循环神经网络结构,具有特殊的记忆结构和门结构增强了长期依赖性的记忆能力,弥补了RNN 的梯度爆炸以及容易忽视时间序列内部的长期依赖关系等问题。因此,本文以LSTM作为预测算法构建PM10浓度预测模型。
研究表明,空气质量主要受污染源的排放与气象条件的影响。在污染源位置固定且污染物排放相对稳定的前提下,气象条件对大气中污染物的累积、消除以及扩散有重要作用。例如,风是影响污染物扩散的主要因素,风速影响大气污染物扩散的速度,而风向影响大气污染物的扩散方向。相对湿度的增加有助于细颗粒物的沉降,从而降低空气中颗粒物的浓度[2]。同时,光化学烟雾的形成也取决于太阳辐射和温度。此外,大气中的颗粒物浓度不仅受某个气象因素的影响, 而且受多种气象因素复杂关联的特殊天气现象的影响。因此,本文利用风速、风向、湿度、温度、大气压5种气象因素和历史PM10浓度数据作为预测模型的输入。在城市中,受区域地形、地貌、排放源位置、排放速率和天气因素的影响,PM10浓度具有很强的非线性和波动性特征。同时,PM10浓度数据在采集过程中因受众多因素干扰会产生噪声,若将采集到的数据直接用来实验仿真,会使模型不能准确地寻找PM10浓度时间序列的变化规律,导致模型预测精度不高。文献[8]采用小波分析技术将PM10浓度时间序列进行分解, 建立了小波变换与支持向量机相组合的PM10浓度预测模型。文献[9]中采用经验模态分解(empirical mode decomposition, EMD)方法对时间序列进行了分解处理,但在使用EMD方法时容易产生模态混叠现象。文献[10]采用整体经验模态分解将PM2.5时间序列进行分解,然后用支持向量回归预测,有效提高了预测精度。集成EMD(ensemble EMD,EEMD)即继承小波变换多变分析的优势, 又改善了EMD的模态混叠现象。CEEMDAN(complete EEMD with adaptive noise,CEEMDAN)在EEMD的基础上进行了改进,不仅克服分解效率低的问题,而且重构误差近乎为0,更适合非线性时间序列的分解。
综上,本文提出1种基于EEMD-样本熵和LSTM的PM10浓度预测模型。利用CEEMDAN将原始PM10浓度时间序列分解为若干个不同复杂度的子序列;基于样本熵判定剩余各子序列的复杂度,将相近的子序列进行合并重组,得到复杂度差异明显的PM10浓度子序列;针对各重组子序列加入气象因素分别建立适当参数空间的LSTM预测模型[11,12];最后将预测值进行叠加得到最终预测值。
1 研究方法
1.1 CEEMDAN方法
EMD由Huang等[13]于1998年提出,该方法可以对原始信号自适应分解出频率不同的固有模式分量(intrinsic model function,IMF),自适应性强。EEMD是在EMD基础上改进的方法[14],主要是将不同的高斯白噪声多次加入原始序列中,然后分别进行EMD分解,最后将得到的IMF分量求均值得到最终结果,避免了模态混叠现象的出现。然而,实际中EEMD方法添加的白噪声经过多次平均后,并未抵消完全。算法依赖于添加的白噪声的幅值和平均次数。CEEMDAN方法通过在每一分解阶段添加自适应白噪声,在较少的平均次数下,实现重构误差几乎为0。因此,CEEMDAN方法既能克服EMD所存在的模态混叠现象,又解决了 EEMD分解的不完整性和必须通过增加平均次数来降低重构误差所造成的计算效率低的问题。
记s(n)为原始PM10浓度时间序列,vi(n)为第i(1,2,…,I)次实验所添加的高斯白噪声序列,第i次分解PM10浓度时间序列可表示为si(n)=s(n)+vi(n)。假设第k个由EMD和CEEMDAN产生的模态分量分别表示为Ek(·)和IMFk,则CEEMDAN算法具体步骤如下:
1)与EEMD方法相同,CEEMDAN针对PM10浓度时间序列s(n)+vi(n),进行I次分解。通过EMD方法计算得到第1个模态分量:
(1)
2)计算由CEEMDAN分解的第1个唯一的余量序列为:
r1(n)=s(n)-IMF1(n)
(2)
3)对r1(n)+ε1E1[vi(n)]进行i(1,2,…,I)次分解。计算得到第2个模态分量为:
(3)
4)同样,对剩余每个阶段,计算第k(2,3,…,K)个余量序列;然后依据步骤3),计算得到第k+1个模态分量,即:
rk(n)=rk-1(n)-IMFk(n)
(4)
(5)
5)执行步骤4),当余量序列不可再分解,即余量信号的极值点个数至多为2时,算法终止。此时,得到K个模态分量,余量序列的最终结果为:
(6)
此时原始PM10浓度时间序列s(n)最终被分解为![]() 和R(n)。
和R(n)。
综上,CEEMDAN分解过程完整,能够对原始PM10浓度时间序列精确重构。
1.2 样本熵
样本熵 (sample entropy, SE)是Richman等[15]在2000年提出的一种能够对时间序列复杂度进行度量的新方法,是对近似熵(approximate entropy,AE)的改进,减少了对时间序列长度的依赖性,可以有效降低近似熵在计算过程中出现的误差。给定PM10历史浓度值序列{x(i)|1≤i≤N},m为模式维数,r为相似容限。样本熵具体计算步骤如下:
1)将原时间序列组成m维向量Z(i),
Z(i)=[x(i),x(i+1),…,x(i+m-1)]
i=1,2,…,N-m+1
(7)
2)定义d[Zm(i),Zm(j)]为向量Zm(i)和Zm(j) (j=1,2,…,N-m+1)之间对应元素差值绝对值的最大值。即:
(8)
3)给定相似容限r(r>0),对每个i值统计d[Zm(i),Zm(j)]<r的数目,记为Bi,计算其与(N-m)的比值,记作![]() 即:
即:
(9)
4)计算(N-m+1)个![]() 的平均值,记为Bm(r),即:
的平均值,记为Bm(r),即:
(10)
5)增加维数到(m+1),重复步骤1)—4),得到Bm+1(r),即:
(11)
样本熵值为:
(12)
6)当N取有限值时,样本熵的估计值记为:
(13)
由上述定义可知,SampEn的值与维数m和相似容限r有关,通常情况下,m=1或2,r=0.1 Std-0.25 Std(其中Std为时间序列x(i)的标准差)。本文取m=2,r=0.2 Std。
1.3 长短期记忆神经网络
RNN是一种前馈神经网络的变体[16],隐含层的信息不仅传递到输出层,还传递到下一时刻的隐含层,能够将之前学习的信息应用于当前节点的计算中。LSTM改进了RNN结构,通过在RNN的记忆模块增加门控制单元来控制当前数据与历史数据的关联程度,使得网络模型实现信息的持久性传递与学习[17]。LSTM的基本单元如图1所示。

图1 LSTM的基本单元
Figure 1 Basic unit of LSTM network
假设xt为t时刻的输入向量,t-1时刻的输出为ht-1,W(f),W(i),W(c),W(o), U(f),U(i),U(c),U(o)和bf,bi,bc,bo分别为权重矩阵和偏置向量,计算过程如下:
1)遗忘门忘记无用的历史信息:
Ft=σ(W(f)xt+U(f)ht-1+bf)
(14)
2)输入门根据输入数据和历史信息进行状态更新:
It=σ(W(i)xt+U(i)ht-1+bi)
(15)
(16)
(17)
3)LSTM最终输出由输出门和单元状态共同确定:
Ot=σ(W(o)xt+U(o)ht-1+bo)
(18)
ht=Ot*tanh(Ct)
(19)
式中:σ为sigmoid激活函数;Ft,It和Ot分别为t时刻遗忘门、输入门和输出门的输出状态;![]() 为t时刻输入的单元状态;tanh为tanh激活函数。
为t时刻输入的单元状态;tanh为tanh激活函数。
1.4 基于CEEMDAN-SE和LSTM的PM10浓度预测模型CEEMDAN-SE-LSTM
PM10浓度预测的CEEMDAN-SE-LSTM模型结构如图2所示,具体步骤如下:
1)获取包含历史PM10浓度和气象参数的建模数据。
2)利用CEEMDAN将原始PM10浓度序列分解得到若干IMF分量和1个趋势分量。
3)分别计算各IMF分量的样本熵值,将样本熵值相近的子序列进行合并重组,得到复杂度差异明显的新子序列。
4)为提高模型的预测精度,在数据送入模型之前将新子序列和气象参数进行归一化处理,即:
(20)
式中:X(i)为原始数据;X′(i)为归一化后的数据。
5)针对各新子序列加入气象因素分别建立相应参数空间的LSTM神经网络预测模型,输出各模型的预测值。
6)将步骤4)得到的n个预测值反归一化处理后,相叠加得到PM10浓度预测结果。
7)将预测结果与实际PM10浓度数据相比,计算误差分析的误差指标。
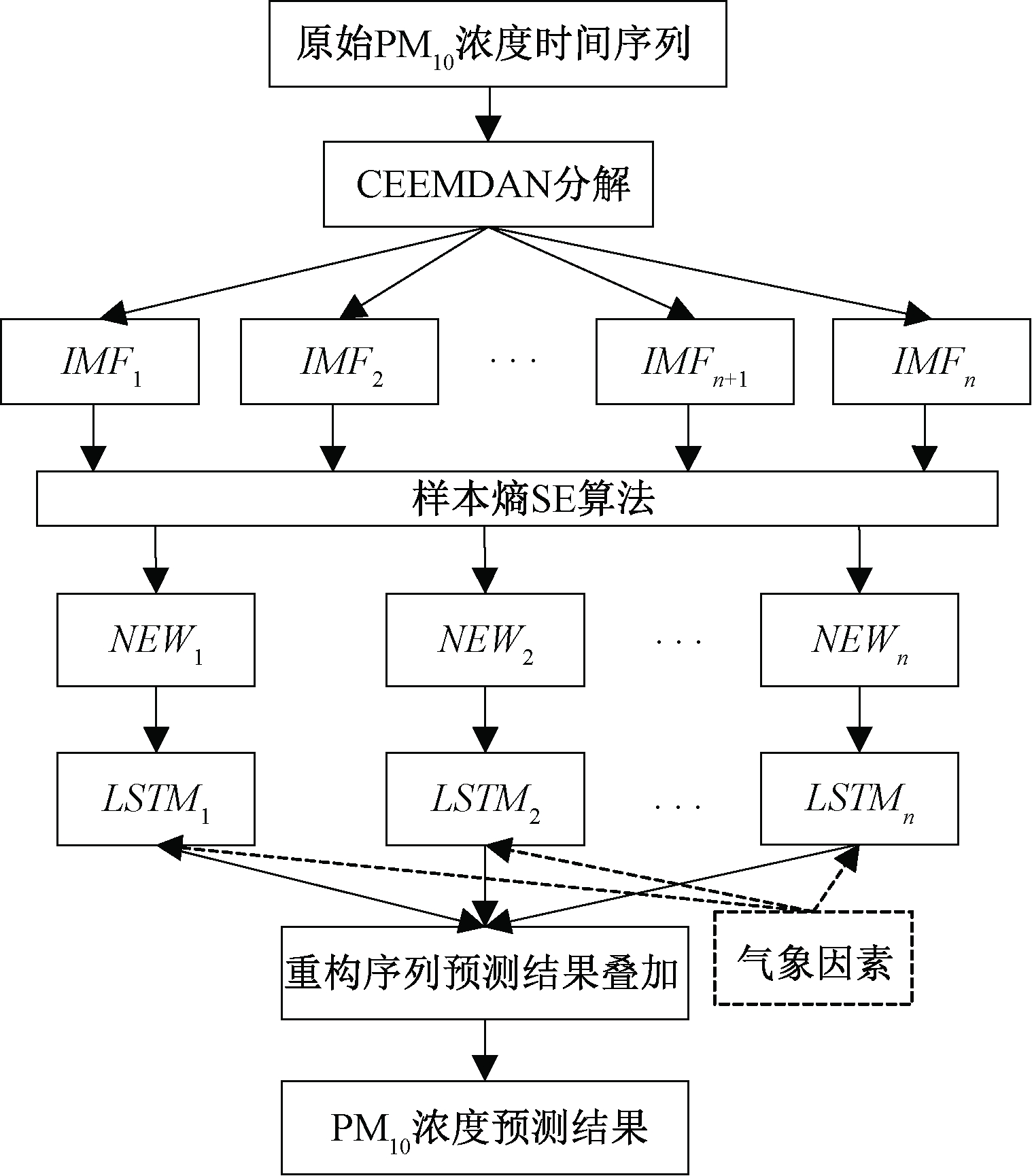
图2 CEEMDAN-SE-LSTM预测模型结构
Figure 2 Structure of CEEMDAN-SE-LSTM forecasting model
2 仿真实验与结果分析
2.1 数据选取
以河北省唐山市的4个空气质量监测站(S1-S4)的PM10浓度实测数据作为研究对象。每1 h采集1次数据,时间跨度为2018-03-01 01:00至2018-05-01 00:00共61 d。对应选取温度(℃)、湿度(%)、风向、风速(m/s)、大气压(mmHg)作为输入的气象参数。将03-01—04-23共计1296组数据作为模型训练样本,04-24—04-30共计168组数据作为模型测试样本。选取监测站S1实测数据的仿真结果作为展示对象。
监测站S1的实测PM10浓度时间序列如图3所示。可知:PM10浓度时间序列具有明显的非线性和波动性特征,这为模型的准确预测增加了难度。
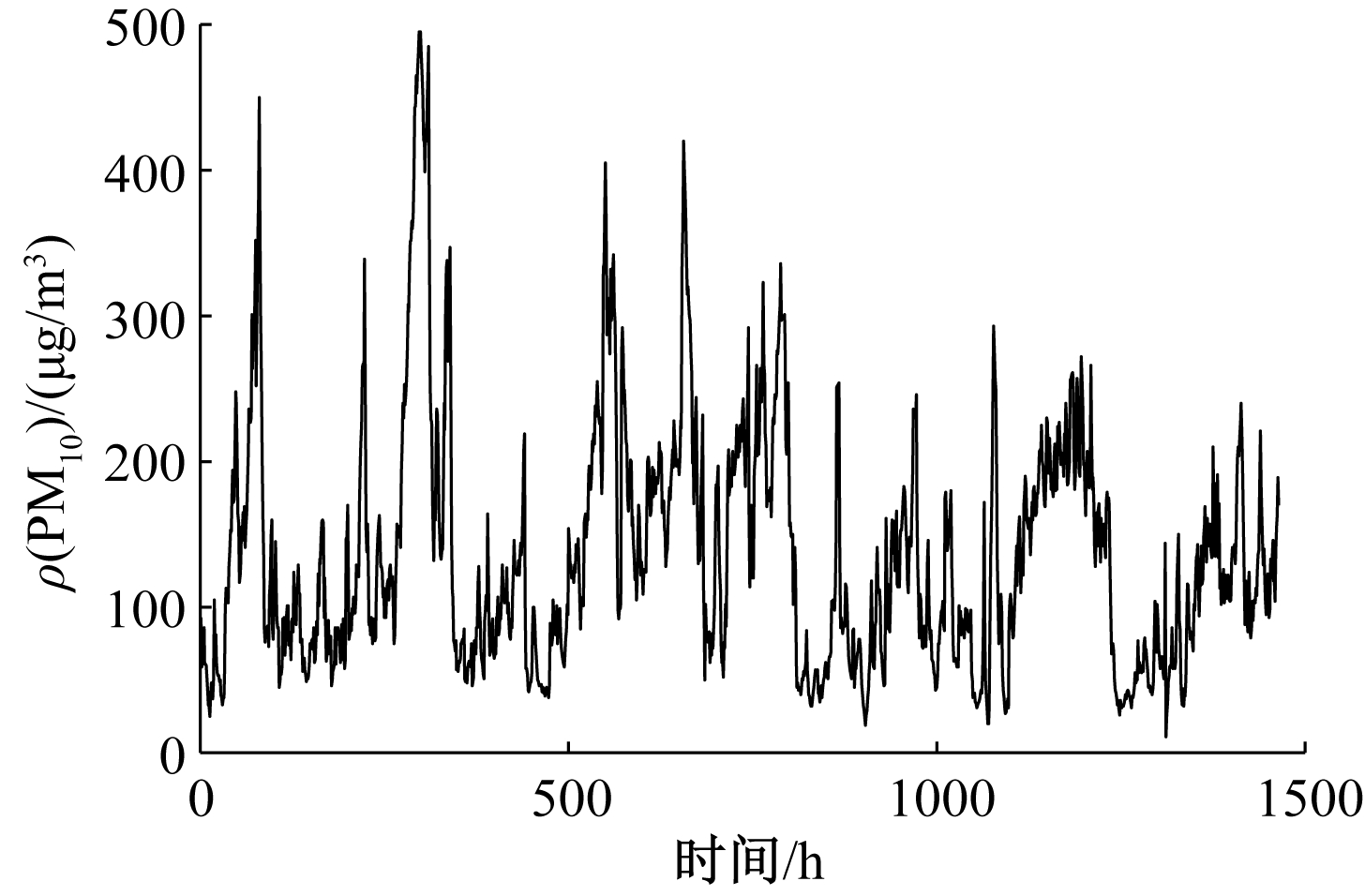
图3 PM10浓度时间序列
Figure 3 Time series of PM10 concentration
2.2 ρ(PM10)时间序列CEEMDAN-SE分解重组
为了更准确地对PM10浓度时间序列进行局部分析,采用CEEMDAN方法对ρ(PM10)时间序列进行分解处理,得到10个IMF分量,如图4所示。

图4 PM10浓度时间序列CEEMDAN分解结果
Figure 4 PM10 concentration time series decomposition
results by CEEMDAN algorithm
为减小计算规模,以更有效地对PM10浓度进行预测,采用样本熵理论对CEEMDAN分解得到的各IMF分量进行复杂度评估,分别计算剩余各分量的样本熵值,结果见表1。各IMF分量的样本熵值的分布如图5所示。
表1 各IMF分量合并后的新子序列
Table 1 New subsequences with merged IMF components

IMFnHSE(n)合并新IMF分量IMF11.321IMF1NEW1IMF20.742IMF2NEW2IMF30.563IMF3、IMF4NEW3IMF40.483IMF50.201IMF5、IMF6、IMF7NEW4IMF60.127IMF70.085IMF80.025IMF8、IMF9、IMF10NEW5IMF90.009IMF100.005
注:HSE(n)为IMFn的样本熵值。

图5 经CEEMDAN-SE处理后的PM10浓度子序列
Figure 5 PM10 concentration subsequences processed by CEEMDAN-SE
如表1所示,为运行效率和运行结果更加精确,综合比较各IMF分量前后差值,高频分量IMF1和IMF2虽然相邻,但其样本熵值差异为0.579,相差较大,故分别作为单独分量;IMF3和IMF4样本熵值相差甚小,因此将其进行合并;IMF5、IMF6和IMF7与IMF8、IMF9和IMF10 2组中各分量之间样本熵值差异均较小,将其分别进行合并。综上,得到5组重组序列,具体合并结果见表1,合并叠加后的新子序列如图5所示。
2.3 预测模型的评价指标
为了评价模型的预测效果,利用平均绝对误差MAE、均方根误差RMSE和平均绝对百分比误差MAPE作为评价指标,分析模型的预测精度。各指标公式如下:
(21)
(22)
(23)
式中:n为测试数据的数量;yi和![]() 分别为PM10的预测值和实际监测值。
分别为PM10的预测值和实际监测值。
2.4 预测结果与对比分析
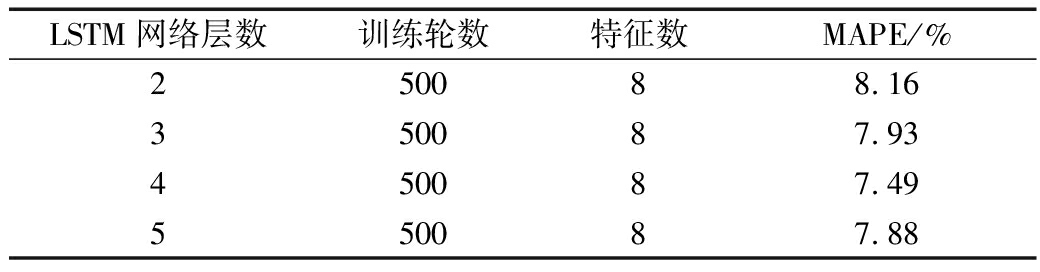
通过实验发现,增加LSTM网络的模型深度可有效改善模型的预测精度。因此,本文分别对不同的LSTM网络层数的模型进行实验,将新子序列的预测时间点前1天、前2天和前3天的数值与预测时间点的气象参数:温度、湿度、风向、风速、大气压作为每个LSTM网络的输入参数,对应预测时间点的新子序列的数值作为模型的输出,实验结果如表2所示。可知:适当增加LSTM网络层数可改善模型的预测精度。因此最终选取LSTM网络包含4个隐含层,每层的神经元个数为5、10、20、40,为防止模型过拟合,Drop Out层设定随机断开20%的神经元。
表2 不同层数的 LSTM网络实验结果
Table 2 Experimental results of different
layers of LSTM networks
LSTM网络层数训练轮数特征数MAPE/%250088.16350087.93450087.49550087.88
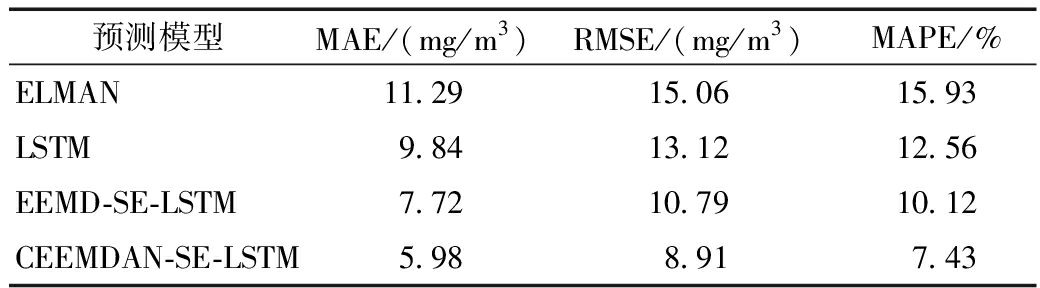
为了验证CEEMDAN-SE-LSTM模型的优越性,在相同的计算环境条件下,构建CEEMDAN-SE-LSTM、EEMD-SE-LSTM、LSTM和ELMAN模型,对比预测效果。其中,EEMD-SE-LSTM和LSTM模型的LSTM网络结构设计与CEEMDAN-SE-LSTM模型相同;ELMAN模型采用单隐含层的网络结构,隐含层神经元个数为12。将预测时间点前1天、前2天和前3天的PM10浓度数值和预测时间点的气象参数:温度、湿度、风向、风速、大气压作为LSTM模型和ELMN模型的输入。各模型的预测结果及实际PM10浓度值如图6所示。预测性能评价指标结果如表3所示。
表3 各预测模型性能指标对比
Table 3 Comparison of prediction performance
indexes for each prediction model
预测模型MAE/(mg/m3)RMSE/(mg/m3)MAPE/%ELMAN11.2915.0615.93LSTM9.8413.1212.56EEMD-SE-LSTM7.7210.7910.12CEEMDAN-SE-LSTM5.988.917.43
由图6可知:CEEMDAN-SE-LSTM模型的预测结果与实际PM10浓度值最为接近,ELMAN模型与实际值的偏离程度最大;LSTM模型拟合程度虽有提高,但相比经过CEEMDAN-SE和EEMD-SE处理过的CEEMDAN-SE-LSTM模型和EEMD-SE-LSTM模型,与实际PM10浓度值偏离程度仍然较大。
由表3可知:CEEMDAN-SE-LSTM模型的平均绝对误差、均方根误差和平均绝对百分比误差均优于EEMD-SE-LSTM、LSTM和ELMAN预测模型。说明CEEMDAN-SE-LSTM模型的预测值能较好地跟踪PM10浓度值时间序列的波动趋势,预测误差最小,预测精度最高,可有效提高PM10浓度预测精度。

![]() —ELMAN;
—ELMAN; ![]() —LSTM;
—LSTM; ![]() —EEMD-SE-LSTM;
—EEMD-SE-LSTM;![]() —CEEMDAN-SE-LSTM;
—CEEMDAN-SE-LSTM; ![]() —实际值。
—实际值。
图6 各模型预测结果
Figure 6 Prediction results of each model
为了验证提出的CEEMDAN-SE-LSTM预测模型的普适性,利用CEEMDAN-SE-LSTM、EEMD-SE-LSTM、LSTM和ELMAN模型分别对唐山市另外3个站点的实测数据进行训练和预测,结果如表4所示。
表4 不同站点数据的各预测模型性能指标对比
Table 4 Comparison of prediction performance indexes of each prediction model for different sites data

预测模型监测站S2监测站S3监测站S4MAE/(mg/m3)RMSE/(mg/m3)MAPE/%MAE/(mg/m3)RMSE/(mg/m3)MAPE/%MAE/(mg/m3)RMSE/(mg/m3)MAPE/%ELMAN12.1615.7816.0311.1915.8915.4511.8815.4316.01LSTM8.9712.8912.878.6312.8712.018.8912.8612.57EEMD-SE-LSTM7.9811.0110.537.6710.9810.027.8310.9410.46CEEMDAN-SE-LSTM6.218.987.875.889.017.126.038.997.88
可知:本文提出的CEEMDAN-SE-LSTM模型对不同站点的PM10浓度预测的结果仍是最优,该模型具有普适性。
3 结 论
针对PM10浓度时间序列具有明显的非线性和波动性特征,提出了CEEMDAN-SE-LSTM模型,通过对唐山市4个监测站的实测PM10浓度数据进行实验研究得到如下结论:
1)利用CEEMDAN将PM10浓度时间序列进行更准确的分解,有利于准确掌握PM10浓度时间序列的变化规律和隐含信息的深度提取。然后基于SE对子序列进行重构,得到复杂度差异明显的PM10浓度子序列,减小了计算规模。
2)采用多层LSTM网络作为预测算法,能更加准确地描述ρ(PM10)的变化趋势,提高了模型的预测精度。
3)将本文提出的CEEMDAN-SE-LSTM模型与其他模型的预测性能进行对比分析,并对不同站点的ρ(PM10)进行预测。结果表明, CEEMDAN-SE-LSTM模型各项指标均优于其他模型,能够有效地拟合ρ(PM10)时间序列的非线性变化,预测精度良好,也具有普适性。
[1] KHANIABADI Y O, GOUDARZI G, DARYANOOSH S M, et al. Exposure to PM10, NO2, and O3 and impacts on human health[J]. Environmental Science and Pollution Research, 2017,24(3):2781-2789.
[2] LI Y, CHEN Q L, ZHAO H J, et al. Variations in PM10, PM2.5 and PM10 in an urban area of the Sichuan basin and their relation to meteorological factors[J]. Atmosphere,2015,6(1):150-163.
[3] VLACHOGIANNI A, KASSOMENOS P, KARPPINEN A, et al. Evaluation of a multiple regression model for the forecasting of the concentrations of NOx and PM10 in Athens and Helsinki[J]. Science of the Total Environment,2011,409(8):1559-1571.
[4] LI W D, KONG D M, WU J. A new hybrid model FPA-SVM considering cointegration for particular matter concentration forecasting: a case study of Kunming and Yuxi, China[J]. Computational Intelligence and Neuroscience, 2017: 2843651.
[5] 冯晓秀,高志文,李风军,等.基于LS-SVR、BP-ANN和 MLR模型的PM10浓度预测[J].中国环境监测,2014,30(6):138-141.
[6] DEDOVIC M M, AVDAKOVIC S, TURKOVIC I, et al. Forecasting PM10 concentrations using neural networks and system for improving air quality [J]. 2016 XI International Symposium on Telecommunications (BIHTEL), Sarajevo, 2016:1-6.
[7] QU X Y, KANG X N, ZHANG C, et al. Short-term prediction of wind power based on deep Long Short-Term Memory[C]∥2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, 2016:1148-1152.
[8] 王平,张红,秦作栋,等.基于wavelet-SVM的PM10浓度时序数据预测[J].环境科学,2017,38(8):3153-3161.
[9] 邓翱,金敏.基于EMD的时标特征提取方法及其在短期电力负荷预测中的应用[J].计算机应用研究,2017,35(10):2952-2955.
[10] 秦喜文,刘媛媛,王新民,等.基于整体经验模态分解和支持向量回归的北京市PM2.5预测[J].吉林大学学报(地球科学版),2016,46(2):563-568.
[11] BAI Y, LI Y, WANG X X, et al. Air pollutants concentrations forecasting using back propagation neural network based on wavelet decomposition with meteorological conditions[J]. Atmospheric Pollution Research,2016,7(3).:557-566.
[12] 郭飞,谢立勇.基于气象因素和改进支持向量机的空气质量指数预测[J].环境工程,2017,35(10):151-155.
[13] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physicaland Engineering Sciences,1998,454(12):903-995.
[14] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1 (1):1-41.
[15] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology Heart Circulatory Physiology,2000,278(6):2039-2049.
[16] GRAVES A, MOHAMED A, HINTON G. Speech recognition with deep recurrent neural networks[C]//Proceedings of International Conference on Acoustics, Speech and Signal Processing Acoustics. Vancouver, Canada:IEEE,2013:6645-6649.
[17] HOCHREITE S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation,1997,9(8):1735-1780.