0 引 言
PM2.5又称为细颗粒物,是指空气动力学当量直径≤2.5 μm的颗粒物。已有研究表明,PM2.5和人体健康之间有密切联系[1]。由于地面监测成本较高,且网络空间分布不均匀,东部多,西部少,高密度的大气监测难以实现,使用卫星气溶胶光学厚度(aerosol optical depth, AOD)来估算地面PM2.5浓度是目前的一个研究热点。1997年,Kaufman等[2]反演了陆地上空的AOD,通过和地面监测网AERONET得到的AOD进行验证,误差为0.05左右。2002年,毛节泰等[3]使用地面观测值验证了北京地区的MODIS 10 km AOD,结果显示两者的相关系数超过0.7。目前利用AOD数据估算地面PM2.5浓度主要有4种方法:基于物理机理的半公式经验法、比例因子法、统计模型法以及机器学习方法,其中机器学习方法[4]精度高,易实现,已被用于大范围PM2.5的估算研究工作。Gupta等[5]将神经网络用于估算美国东南部地面PM2.5浓度,结果表明,机器学习相对于统计模型潜力巨大。Liu等[6]使用随机森林算法,建立了美国地面PM2.5浓度估算模型,得到了美国高分辨率的地面PM2.5浓度分布。Hu等[7]利用PM2.5和AOD之间空间上的关系,建立了地理加权的回归模型。考虑到时间因素的影响,Fang等[8]提出一种时序结构自适应模型,利用AOD估算全国PM2.5浓度,验证结果R2=0.80。Li等[9]将地理信息与DBN相结合,建立了地理智能的深度置信网络,在全国区域的PM2.5浓度估算中取得了较好的效果。但是,PM2.5浓度与多方面因素有所联系,当前大多数研究使用单一学习器估算地面PM2.5浓度,其中线性回归对于非线性以及特征空间大的数据时性能表现不足;神经网络面临着容易陷入局部最优解以及迭代收敛速度慢的问题,且容易陷入过拟合,导致使用传统的机器学习模型估算地面PM2.5浓度的难度增加,传统机器学习模型在地面PM2.5浓度估算研究中存在较大改进空间。
为解决上述问题,本文提出使用MODIS 10 km AOD数据估算地面PM2.5浓度,可有效弥补地面PM2.5监测站点在空间覆盖上的不足,为研究PM2.5动态变化提供了大范围、长时间的基础数据。在建立估算模型方面采用Stacking集成框架将随机森林、梯度提升回归树以及XGBoost进行集成。与传统回归模型相比,随机森林避免了支持向量机对于核函数的依赖以及线性回归对于预先函数的设定,梯度提升回归树和XGBoost则可用于大多数的线性以及非线性回归问题,能够适应各种类型的数据,且相比于神经网络,XGBoost使用二阶导数以及正则化方法,大大提高了训练速度,不易陷入过拟合。由于Stacking结合多种机器学习算法,克服单个模型的缺陷,因此Stacking在许多应用方面取得了较好的效果[10,11]。现有研究中用于估算地面PM2.5模型都为单学习器模型,时间参数、气象参数以及与PM2,5排放相关参数对污染物的扩散与稀释有很大的影响[12,13]。因此,本文提出以Stacking方法构建地面PM2.5浓度估算模型,上述参数作为估算因子,对PM2.5浓度变化的时间规律以及与气象参数的相关性进行分析,结合改进网格搜索[14],优化模型超参数,并对比多个模型的差异,从而获取更准确、稳定的结果。
1 数据构建与分析
本文所选研究区域是整个中国区域,研究时间为2016-01-01—12-31。
数据源包括5个部分:1)地面PM2.5。地面PM2.5浓度数据来源于中国环境检测中心站(http://www.cnemc.cn),地面监测站点数约1500个,采用地面PM2.5浓度日均值用于模型构建。2)中分辨率成像光谱仪(MODIS) 10 km AOD。Terra和Aqua卫星的MODIS AOD值来源于 (LAADS Web, https://ladsweb.modaps.eosdis.nasa.gov/),采用Terra和Aqua卫星的MODIS AOD数据平均值用于估算地面PM2.5浓度值。3)气象参数。相对湿度(RH,%)、2 m处空气温度(TMP,K)、地面以上10 m风速(WS, m/s)、表面压力(PS, kPa)和行星边界层高度(PBL, m)通过WRF(the weather research and forecast model)模拟得到。4)MODIS归一化植被指数(normalized difference vegetation index, NDVI)。来源于LAADS网站。5)人口和土地数据。人口数据来源于社会经济数据和应用中心(SEDAC, http://sedac.ciesin.columbia.edu/data/collection/gpw-v4);土地数据来源于(land-use and land-cover change, LUCC)中科院环境数据云平台。
1.1 时间特征对PM2.5的影响
研究区域跨经纬度较广,气候类型多样,不同气象条件对PM2.5浓度影响明显,不同时间、不同季节的天气状况不尽相同,因此,研究长时间序列的PM2.5浓度变化规律十分有必要。
本文利用2016年全年的地面PM2.5浓度数据进行时间变化规律的分析,结果如图1所示。由图1a可知:PM2.5在1、2、3、11、12月的浓度值较高。这是由于这些月份气温较低,大气边界层较低,大气湍流活动较弱,气溶胶更容易聚集在近地面,且在冬季部分地区进入采暖季,煤炭燃烧造成污染物排放加重,导致与其他月份PM2.5浓度值的明显差异。由图1b可知:夏季PM2.5浓度为一年当中最低,因夏季高温多雨,大气湍流活动强,有利于PM2.5的扩散和清除。
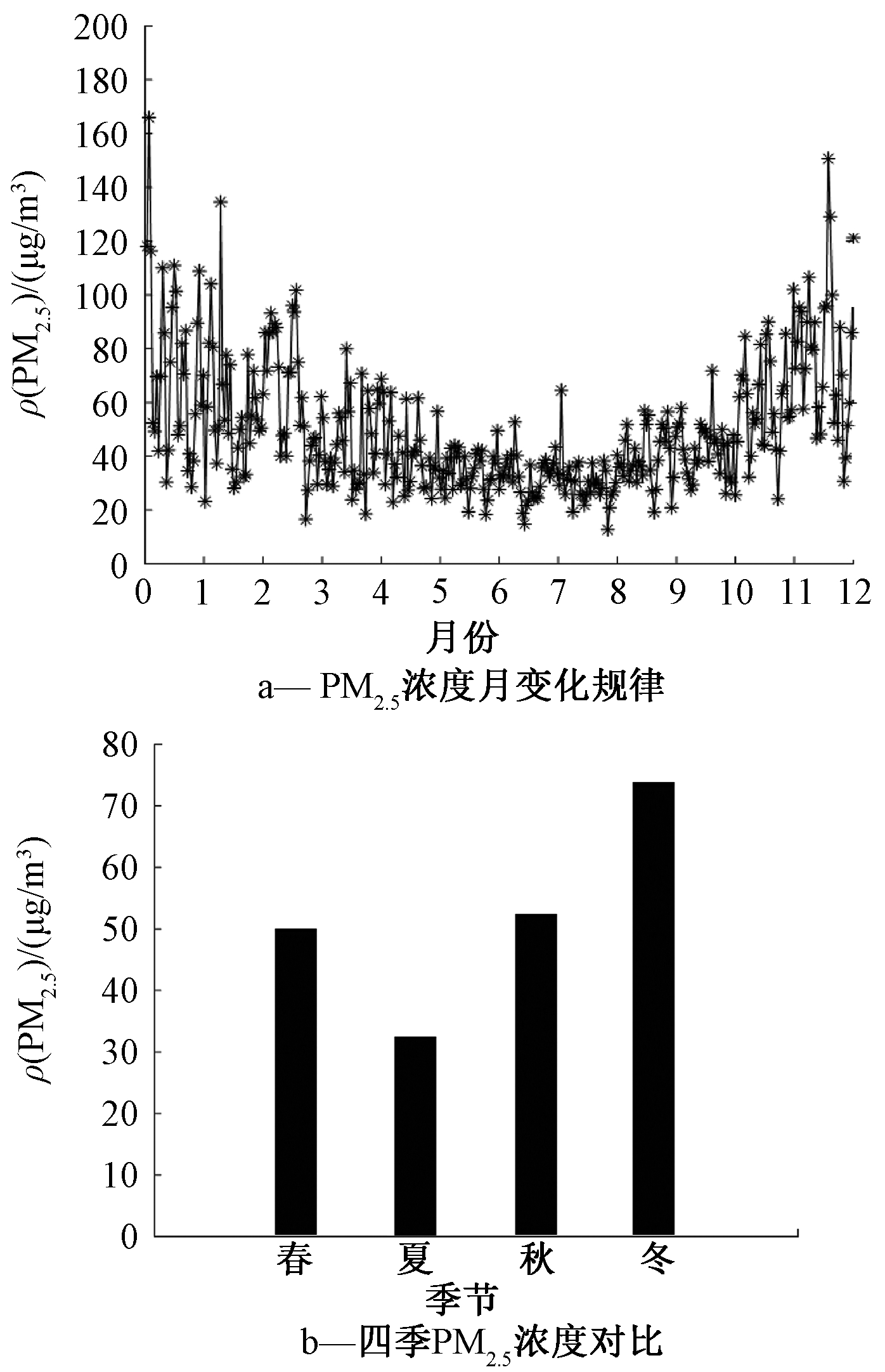
图1 全国PM2.5浓度时序规律
Figure 1 The time series analysis result of PM2.5 concentration
1.2 气象特征对PM2.5的影响
除了人为、自然污染源排放等内部因素,气象条件等外部因素也是造成大气污染的重要因素,不同气象条件对PM2.5的扩散和清除能力不同。
2016年地面PM2.5浓度与气象特征的相关性分析结果如表1所示。可知:6种气象因子与PM2.5存在一定程度的直接相关性,其中PM2.5与温度、风速、压力直接相关性较明显,与表面气压、相对湿度、边界层高度直接相关性较弱,与表面气压、压力和相对湿度呈正相关。而同边界层高度、风速和温度呈负相关,其中气温较高时,大气对流显著,有利于PM2.5扩散,反之出现逆温层不利于PM2.5扩散;风速是影响颗粒物的重要因子,风速越大,污染物的输送和扩散能力越强,污染物浓度就越低,反之污染物浓度越高。
表1 PM2.5浓度与气象特征相关系数
Table 1 The correlation coefficients between
PM2.5 and meteorological data
气象因子温度风速表面气压压力相对湿度边界层高度相关系数-0.17-0.270.060.120.04-0.04
1.3 数据预处理
PM2.5数据由多个部分组成,每个特征具有不同的量纲和数量级,特征之间水平相差很大。其中,数值较高的特征,例如,人口数据最大值为33236,最小值为0;数值较低的特征,例如AOD数据,AOD数据最大值为4.993,最小值为0。如果使用原始特征进行分析,数值较高的特征会对模型的建立产生较大的影响,从而削弱数值水平较低特征对于模型的贡献。因此,为了保证输出结果的稳定性与可靠性,对原始特征进行标准化处理,采用标准差标准化(Z-score)公式如式(1)所示:
x*=(x-μ)/σ
(1)
式中:x为数据样本初始值;μ为所有数据样本均值;σ为数据样本标准差;x*为标准差标准化后数据样本值。
标准差标准化其实质是一种线性变换,不会改变原始数据的数值排序,通过标准差标准化,将特征转换为平均值为0、标准差为1的标准正态分布,消除因不同量纲引起的误差,使各特征处于同一个数量级别,在数值上有更强可比性,避免了数值过高/低的特征引发的数值问题,最终结果显示,经过标准化后模型估算表现有较大提高,提升了模型估算性能。
2 Stacking整体架构设计
2.1 构建随机森林估算模型
随机森林(random forest,RF)是Bagging一个扩展变体。随机森林在以分类回归树作为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机特征的选择。本文采用随机森林的回归方法作为构建Stacking模型的基础学习器模型之一,构建过程为:1)对PM2.5训练样本集采用Bootstrap抽样得到m个训练样本的新样本数据集;2)对上述m个样本数据集建立决策树,在建立过程中,从随机选取的部分特征中选取最佳特征进行数据划分;3)重复步骤1和步骤2,构建T棵回归树,形成森林;4)对于T棵树生成的结果,采用均值(回归)方式作为最终的结果。
使用Bagging代表方法中的随机森林作为第1层基学习器之一,通过Bootstrap有放回地抽取样本子集,使每棵树的建立是不同的并且完全公平的,在一定程度上使模型具有较大差异,降低了模型相关性。同时,通过随机选择特征子集,再次降低了模型之间的相关程度,进而使方差进一步降低。随机森林面对默认数据以及不平衡数据表现比较稳健,且具有处理高维特征估算地面PM2.5数据的能力。
2.2 构建GBRT以及XGBoost估算模型
梯度提升回归树(gradient boost regression tree,GBRT)是一种Boosting算法,GBRT中的基学习器是分类回归树,每个子模型是根据已训练出的学习器的性能(残差)训练出来的,是为了减少上一次的残差,使之前的模型的残差往梯度方向减少,在残差减少的梯度方向上建立一个新的模型。GBRT可用于大多数的线性以及非线性回归问题,能处理空间外的异常数据,且适应各种类型的数据,不需要复杂的特征工程,所以将其作为基础学习器之一。
XGBoost(extreme gradient boosting)是在Gradient Boosting框架下实现机器学习算法,由于Boosting算法通过串行生成基学习器,难以实现并行运算而开发出,是由Gradient Boosting Machine的一个C++实现,并在原有的基础上加以改进,从而极大地提升了模型训练速度和预测精度。由于XGBoost实现原理与GBRT类似,两者差异性主要为:1)XGBoost对代价函数进行了二阶泰勒展开,同时用到一阶和二阶导数,使其在训练集上更快收敛,大大提高了训练速度;2)当特征值存在缺失时,XGBoost可以根据增益自动划分分裂方向,对稀疏数据的处理有优势;3)XGBoost在代价函数里加入了正则项,用于降低模型的复杂度,学习出来的模型更加简单,增强了模型的泛化能力,还能在一定程度上降低过拟合的风险;4)XGBoost借鉴了随机森林的做法支持特征抽样,在减少计算量的同时降低过拟合。
由于XGBoost高效的设计实现,使其在面对大量PM2.5数据时大大提高了算法的效率,同时降低了偏差,因此将XGBoost作为基础学习器之一。
2.3 构建Stacking模型
堆叠(Stacking)是通过训练高级学习器来寻找基学习器的最优组合,而不是将若干初级学习器结果进行简单融合。相较于Bagging和Boosting框架使用同类型的基学习器进行构建,Stacking则是将不同类型的基学习器进行组合构建,因为不同类型基学习器对于数据空间以及结构的学习存在较大差别,不同类型基学习器可以从不同的角度观测数据特征,更加全面地学习数据,从而得到一个更准确的结果。核心思想是对基学习器(base learner)进行交叉验证训练,然后在基学习器输出结果的基础上,构造二级特征用于训练元学习器(meta learner)。
2.3.1 多重共线性分析
第2层元学习器特征是由基础学习器交叉验证计算组合得来,相较于原始特征,属于强相关类型的特征。由于二级特征与估算值之间线性相关,计划采用多元线性回归作为第2层元学习器,但将二级特征数据放入元学习器进行训练之前,有必要检验各特征之间是否存在多重共线性问题。
多重共线性不仅会降低回归模型的稳定性和准确性,而且会导致回归模型过拟合。多重共线性一般由容忍度、方差膨胀因子(variance inflation factors,VIF)、特征值等来进行判别。本文选取容忍度及VIF进行判定。
容忍度是指将每个特征值作为预测值对其他特征回归建模时得到的残差比例,用决定系数(R2)表示,值域为[0,1]。VIF通过检查指定特征能够被回归方程中其他特征所解释的程度来检测多重共线性,具体步骤如下。
1)设原方程为:
Y=β0+β1X1+β2X2+…+βkXk+μ
(2)
式中:Xi为输入特征;Y为输出结果;βi和μ为回归系数。
2)计算K个不同的VIF,每1个特征值对应1个VIF,对式(2)中所有特征变量进行最小二乘回归(OLS),计算其决定系数,例如,若i=1,则回归方程为:
X1=α0+α2X2+α3X3+…+αkXk+ν
(3)
3)计算VIF:
(4)
式中:![]() 为第2步中OLS决定系数。
为第2步中OLS决定系数。
4)分析多重共线性程度。多重线性指标统计如表2所示,根据经验法则,当VIF<10,不存在多重共线性;当VIF≥10或容忍≤0.1,则说明特征之间存在较严重的多重共线性。由表2可知:经过第1层基学习器交叉验证计算得到的二级特征之间存在较强的多重共线性。
表2 多重共线性指标统计信息
Table 2 The statistics index of multi-collinearity

模型容差VIFRF0.02638.604GBRT0.03231.639XGBoost0.02736.781
2.3.2 构建岭回归元学习器模型
岭回归,又称及洪诺夫正则化,实质上是通过改良最小二乘法,放弃最小二乘法的无偏性产生有偏估计,允许以损失部分信息、降低精度为代价获得更实际更可靠的回归系数,是一种专用于处理共线性数据的有偏回归方法。岭回归与多元线性回归唯一不同点在于代价函数差别,岭回归在代价函数后加上所有参数的平方和![]() 即L2范数。
即L2范数。
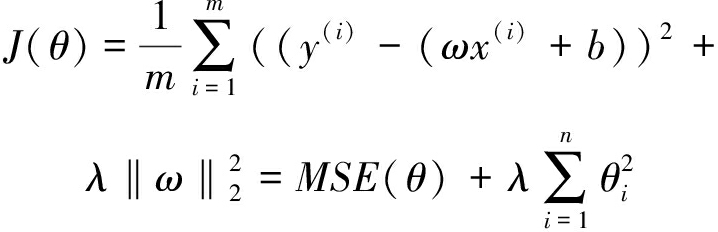
(5)
式中:m为样本数;n为特征数;ω为长度为n的向量,不包含截距项的系数θ0,θ是长度为(n+1)的向量,包含截距项的系数。
由于岭回归代价函数仍然为一个凸函数,利用梯度等于0,求得全局最优解:
θ=(XTX+λI)-1(XTy)
(6)
与多元线性回归代价函数相比,多一项λΙ,其中Ι为单位矩阵。因为特征之间存在较强的共线性,|XTX|接近于0,即XTX接近于奇异矩阵,参数计算结果会不准确,加入λΙ之后可以保证可逆,减少(XTX)-1计算误差。由于特征之间多重共线性的影响,使多元线性回归缺乏稳定性与可靠性,岭回归通过损失了无偏性,对最小二乘回归进行补充,换取较高的数值稳定性,从而得到较高的计算精度。且岭回归建模速度快,不需要复杂的计算过程,在大数据量估算PM2.5的情况下依然运行很快,通过第1层基学习器交叉验证计算,用于岭回归建模数据无异常值的存在,最终选择岭回归作为第2层元学习器。
2.3.3 Stacking集成
Stacking集成方法集成多种学习器的预测结果。本文采用随机森林、GBRT和XGBoost 3种模型作为基学习器,岭回归作为元学习器进行融合得到集成模型,然后用于估算地面PM2.5浓度。通过对多种机器学习算法的结合,克服单个模型缺陷,优化岭回归的输入,提升了估算结果。Stacking模型融合过程如图2所示,算法步骤如下:

图2 Stacking 模型结构
Figure 2 The structure of stacking model
1)获取初始数据集,采用90%的数据集作为训练集,10%的数据集作为测试集。
2)Stacking选用随机森林、GBRT和XGBoost作为第1层基础学习器,采用5折交叉验证来训练第1层模型,每个模型计算得到与原训练集数量相当的数据,3种模型扩展之后生成第2层特征,输入到元学习器岭回归模型,岭回归学习3种算法输出结果与PM2.5浓度之间的关系,生成回归模型用于后续估算。
3)Stacking在3个基学习器模型进行5折交叉验证过程中,对测试集进行5次计算,将5次计算得到的结果平均,计算得到与原测试集数量相当的数据,3种模型扩展之后生成第2层测试集,输入到元学习器岭回归模型。
4)将得到的新训练集用于训练第2层元学习器岭回归模型,并用新的测试集验证Stacking模型性能。
5)融合3种算法得到Stacking模型,实现对全国地面PM2.5浓度的估算。
3 结果及分析
3.1 模型性能分析
为了比较模型性能,本文选取了3种评价回归模型的的性能指标,依次是平均绝对误差(MAE)、均方根误差(RMSE)和决定系数(R2),其计算如式(7)—(9)所示:
(7)
(8)
(9)
式中:Yi为第i个样本的真实值;![]() 为第i个样本的预测值;
为第i个样本的预测值;![]() 为预测值的平均值;n为样本容量。MAE反映输出值误差的实际情况,RMSE反映模型输出值的稳定性,二者的值越小,模型性能越好。R2反映模型输出值与实际值的相关程度,其值越接近1,说明模型的效果越好。
为预测值的平均值;n为样本容量。MAE反映输出值误差的实际情况,RMSE反映模型输出值的稳定性,二者的值越小,模型性能越好。R2反映模型输出值与实际值的相关程度,其值越接近1,说明模型的效果越好。
3.2 实验结果
2016-01-01—12-31的数据共183140条,其中90%的数据作为训练集,10%的数据作为测试集,利用2.3.3节中的模型估算地面PM2.5浓度,结果如图3所示。可知:由随机森林、GBRT、XGBoost和岭回归融合得到的Stacking模型的各方面性能指标均优于基学习器中表现最好的XGBoost,Stacking决定系数为0.87,对比于XGBoost、GBRT、随机森林提高量分别为0.01、0.02和0.05,平均提高约0.03。Stacking平均绝对误差为11.24 μg/m3,降低量分别为0.52,1.07,2.48 μg/m3,平均降低1.4 μg/m3。Stacking均方根误差为20.53 μg/m3,降低量分别为0.66,1.17,3.57 μg/m3,平均降低1.8 μg/m3。4种模型拟合斜率都<1,说明模型都存在一定程度偏差,但Stacking的斜率为0.85,相比随机森林、GBRT、XGBoost 3种基学习器模型,分别降低了3%、5%、10%的偏差。

图3 地面PM2.5浓度估算结果
Figure 3 Ground PM2.5 concentration estimation results
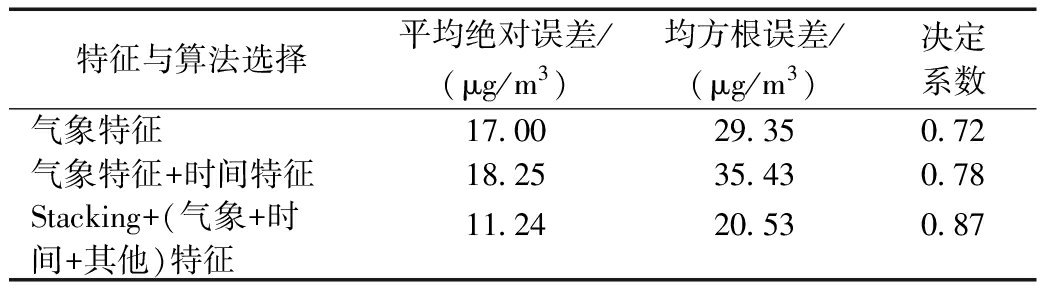
为验证本文所选特征的有效性,分别使用不同的特征和算法组合构建不同回归模型,并进行测试,结果如表3所示。可知:每加入1个特征或者算法,PM2.5估算结果都会得到显著提升。
表3 特征与算法选择效果对比
Table 3 The performance contrast of
features and algorithms
特征与算法选择平均绝对误差/(μg/m3)均方根误差/(μg/m3)决定系数气象特征17.0029.350.72气象特征+时间特征18.2535.430.78Stacking+(气象+时间+其他)特征11.2420.530.87
本文也利用其他机器学习模型进行训练和测试,结果如表4所示。可知:相对于没有使用集成策略机器学习模型,以分类回归树作为基学习器,分别使用Bagging集成的随机森林和Boosting集成的GBRT以及XGBoost,各种模型性能指标有较大提升,集成策略对于单学习器模型的结果而言有较好表现。与此同时,对于使用不同集成学习框架的XGBoost、GBRT和RF,本文提出的Stacking回归模型在3种评价指标中有明显提升,表明本文所提出的回归模型与其他模型相比,模型表现更优。
表4 各算法效果对比
Table 4 The performance contrast of different algorithms

模型平均绝对误差(μg/m3)均方根误差/(μg/m3)决定系数线性回归26.3647.000.30支持向量机18.2535.430.59决策树19.5636.800.63神经网络19.4531.490.68随机森林13.7224.100.82GBRT12.3121.700.85XGBoost11.7621.190.86本文方法11.2420.530.87
3.3 2016年PM2.5浓度分析
图4为由Stacking模型估算结果经计算得到的PM2.5年均值与地面站点测量年均值对比,可知:两者具有相似的空间分布,证明了模型估算结果的可靠性。在Stacking模型得到的结果中,北方地区PM2.5浓度水平高于南部地区,华北平原是1个污染比较严重的地区,正如Chen等[15]研究所提到的,该地区污染物排放严重,天气停滞,风力弱是该地区PM2.5严重污染的主要原因。此外,湖南和湖北地区的PM2.5浓度通常较高,研究指出,造成此地区PM2.5浓度较高的原因是湖南和湖北部分地区工业基础雄厚、污染排放集中[16,17]。且由于地理条件的优势,东南沿海地区PM2.5浓度较低,同时PM2.5污染最少的地区是海南省和云南省[18],这得益于人为排放量低和良好的大气扩散条件[19]。在西北地区,特别是新疆维吾尔自治区有极高PM2.5污染,可能原因是沙漠地区的沙尘颗粒对PM2.5的累计有较大贡献[20]。

图4 全国PM2.5均值分布模型估算与地面站点测量结果
Figure 4 The annual mean distribution of derived PM2.5 and ground-measured PM2.5 in China
4 结 论
PM2.5污染是我国当前大气污染治理方面的主要问题,本文针对PM2.5无法进行大范围高密度地理监测,提出了基于卫星AOD数据和Stacking方法来估算地面PM2.5浓度值,并通过引进时间参数、气象参数以及与PM2.5排放相关的其他参数进行建模优化。结果表明:Stacking结合了多种学习器的优势,相比于其他集成学习框架以及单一学习器,Stacking在提升模型的泛化能力以及提高模型性能方面优势显著,集成多种模型的思想,进一步提高了模型整体效果。本文以2016年全年数据作为实验数据,利用本文所提出的方法进行模型训练和测试,验证了Stacking模型在估算地面PM2.5浓度方面有较好的性能表现,满足了估算地面PM2.5的精度要求,可以对大范围地理区域进行大气污染监测,达到了预期目的。鉴于本文所提到的方法在Terra和Aqua卫星的MODIS 10 km AOD产品上表现良好,将其用于更高分辨率的AOD产品(如MODIS 3 km AOD 数据)或者静止卫星的AOD产品,以满足对精度要求更高的小范围地理区域或者城市区域地面PM2.5浓度研究,将是今后工作重点。
[1] 亢红霞,那晓东,臧淑英. 基于卫星遥感数据(AOD)估算PM2.5的研究进展[J]. 环境科学与管理, 2016, 41(2): 30-34.
[2] KAUFMAN Y J, TANRÉ D, REMER L A, et al. Operational remote sensing of tropospheric aerosol over land from EOS moderate resolution imaging spectroradiometer[J]. Journal of Geophysical Research Atmospheres, 1997,102(27):17-51.
[3] 毛节泰, 李成才. MODIS卫星遥感北京地区气溶胶光学厚度及与地面光度计遥感的对比[J]. 应用气象学报, 2002,13(1):127-135.
[4] XI X, WEI Z, RUI X G, et al. A comprehensive evaluation of air pollution prediction improvement by a machine learning method[C]//IEEE International Conference on Service Operations & Logistics. IEEE, 2016.
[5] GUPTA P, CHRISTOPHER S A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: multiple regression approach[J]. Journal of Geophysical Research Atmospheres, 2009,114(20).
[6] LIU Y, CAO G F, ZHAO N Z, et al. Improve ground-level PM2.5 concentration mapping using a random forests-based geostatistical approach[J]. Environmental Pollution, 2018,235:272-282.
[7] HU X F, WALLER L A, AL-HAMDAN M Z, et al. Estimating ground-level PM2.5 concentrations in the southeastern U.S. using geographically weighted regression [J]. Environmental Research, 2013, 121(2): 1-10.
[8] FANG X, ZOU B, LIU X P, et al. Satellite-based ground PM2.5 estimation using timely structure adaptive modeling[J]. Remote Sensing of Environment, 2016, 186: 152-163.
[9] LI T W, SHEN H F, YUAN Q Q, et al. Estimating ground-level PM2.5 by fusing satellite and station observations: a geo-intelligent deep learning approach[J]. Geophysical Research Letters, 2017, 44(23).
[10] 张璞,刘畅,王永. 基于特征融合和集成学习的建议语句分类模型[J]. 山东大学学报(工学版), 2018, 48(5): 47-54.
[11] 张笑铭,王志君,梁利平. 一种适用于卷积神经网络的Stacking算法[J]. 计算机工程, 2018, 44(4): 243-247.
[12] CHEN J, LU J, AVISE J C, et al. Seasonal modeling of PM2.5 in California’s San Joaquin Valley[J]. Atmospheric Environment, 2014, 92:182-190.
[13] ZHANG C, NI Z W, NI L P. Multifractal detrended cross-correlation analysis between PM2.5 and meteorological factors[J]. Physica A: Statistical Mechanics and its Applications, 2015, 438:114-123.
[14] 温博文,董文瀚,解武杰,等. 基于改进网格搜索算法的随机森林参数优化[J]. 计算机工程与应用, 2018, 54(10): 154-157.
[15] CHEN Z H, CHENG S Y, LI J B, et al. Relationship between atmospheric pollution processes and synoptic pressure patterns in northern China[J]. Atmospheric Environment, 2008, 42(24): 6078-6087.
[16] 陈楠,操文祥,丁青青,等. 湖北省PM2.5与PM10比值分析及PM2.5时空分布特征研究[J]. 环境科学与管理, 2017, 42(1): 98-102.
[17] 王婷. 长株潭地区PM2.5时空分布研究[D].湘潭:湖南科技大学,2016.
[18] 王振波, 方创琳, 许光, 等. 2014年中国城市PM2.5浓度的时空变化规律[J]. 地理学报, 2015, 70(11): 1720-1734.
[19] 李沈鑫, 邹滨, 刘兴权, 等. 2013—2015年中国PM2.5污染状况时空变化[J]. 环境科学研究, 2017,30(5):678-687.
[20] 姜磊, 周海峰, 赖志柱, 等. 中国城市PM2.5时空动态变化特征分析:2015—2017年[J]. 环境科学学报, 2018, 38(10):33-42.