0 引 言
城市水体水质的优劣是影响城市水环境的重要因素之一。近些年来,随着我国工业化和城镇化进程的加快,城市中污水的排放也急剧增加[1]。城市污水是指城市在运作过程中产生的生活污水、工业废水以及径流污水汇聚后的总和。郑利杰[2]等应用内梅罗指数法对我国27个典型城市进行水质分析后得出,我国当前城市地表水体中浓度超标的污染物主要为氨氮、总磷、COD以及BOD5。BOD5是当前对于地表水、生活污水以及大部分工业废水进行监控的必测指标之一[3]。实现对BOD5快速、准确的测定有助于相关部门加强对城市总体水环境的监管。
当前行业对于BOD5测定的通常方法是采用标准稀释法。使用标准稀释法进行测量虽然操作流程简单,但由于测量的完全离线进行,会造成测量时间的延误,使测量结果产生误差[4]。而且由于需要5天的测量延迟时间,标准稀释法不适用于对BOD5的实时监控。当前对于BOD5的在线测量技术主要是使用生物传感器实现的。但由于自身机理原因,生物传感器的维护工作复杂、花费昂贵。解决这类问题可从硬件及软件两个方面入手。相比于硬件的开发周期长、成本高等问题,通过改进算法使用软测量的方式对BOD5进行测定,成本更低。Scott[5] 对于解决BOD5测定问题提出了一种基于机理模型的软测量方法,但由于该机理模型存在大量需辨识的参数,在实际应用过程中比较繁琐。目前其他方法主要是通过构建人工神经网络的形式实现的。Mirbagheri[6]等使用了RBF神经网络对出水BOD5浓度进行了预测,取得了较为准确的结果,但其网络结构需人工确定。王树东等[7]提出了基于混合遗传算法优化RBF神经网络的软测量方法,对网络结构及参数进行了优化,但由于其自身机理问题导致计算复杂、训练时间较长。目前使用人工神经网络主要存在两个问题:其一是所构建人工神经网络结构复杂,训练所需的计算量大,泛化性较弱;其二是神经网络的训练需要较多的样本数据,这与当前BOD5的测量原理不相符。因此本文提出了建立GA-SVR预测模型的方式对BOD5进行软测量。相比于神经网络,SVR模型所需的训练样本较小,学习难度较低,具有更好的泛化性。通过使用遗传算法对支持向量机回归模型进行改进,解决其参数不易选取的缺点。通过对模型输入较易测得的参数并以此输出BOD5的形式得到BOD5数值。该模型泛化能力较强,更加适用于样本数据较少的环境。
1 模型算法介绍
根据水质参数数据小样本的特点,本文提出了基于GA改进SVR参数的预测模型。SVR模型具有较好的非线性预测能力,一直以来都是机器学习领域的热点[8],且SVR具有适应小样本数据的优点,因此相比于其他算法更加适用于水质的预测。遗传算法具有良好的并行性、鲁棒性及全局最优性[9]。通过遗传算法的全局搜索能力对SVR的3项参数进行寻优,建立数学模型,使用模型得到预测值。
1.1 支持向量机回归
SVR(支持向量机回归)预测算法是Vapnik[10]等提出的支持向量机原理在数据回归预测方面的应用。SVR的核心思想是风险最小化原则,其原理是通过构建非线性映射,将原始数据集映射至高位甚至无穷维的一个新的特征空间中。在此空间中可以找到一个线性函数,这个线性函数可以构建出输入值与输出值间的数学关系,通过这个函数得到预测值,该函数可以用式(1)表示:
f(x)=ωTφ(x)+b
(1)
式中:φ(x)为原始易测输入水质数据到高维空间的非线性映射;ω为特征向量。
由式(1)可以得到形式(2)的代价函数:
(2)
式中:C被称作惩罚函数,惩罚函数的值决定回归函数对于数据的拟合程度,当C选取过大时会使拟合函数产生过拟合的现象,当参数C选取过小时又会出现欠拟合的现象。式(2)中|yi-f(xi)|为真实数据与输出数据的差值。定义ε为不敏感损失函数,当|yi-f(xi)|>ε时计算损失。通过引入不敏感损失函数使误差得到控制。对于代价函数的风险最小化求解,可以转化为形如式(3)的目标函数:
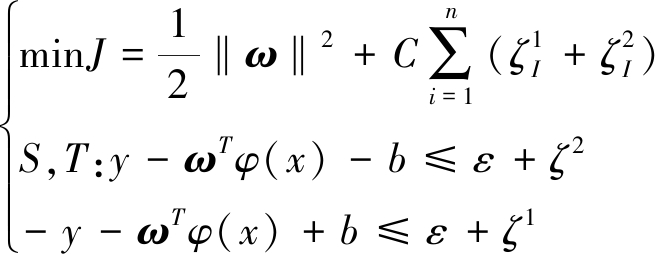
(3)
式中:ζ1与ζ2为松弛变量。通过引入拉格朗日乘子算法,在KKT条件下,为每个约束条件加上一个拉格朗日乘子,通过定义拉格朗日函数,将约束条件融入到目标函数之中得到式(4):
(4)
式中:α为大于0的拉格朗日乘子;K(xi,xj)为满足Mercer条件的核函数。经过试验对比,本文采用径向基核函数作为核函数,模型的输出预测值可用式(5)表示:
(5)
式中:σ为核函数参数;xi和xj分别训练集输入参数与测试集输入参数。
1.2 GA参数优化算法
遗传算法(genetic algorithms, GA)是通过模拟自然界中“适者生存”法则原理发展起来的随机全局搜索优化算法。遗传算法将生物染色体编码的机制适用到对优化目标参数组的编码中,使用二进制数组或实数表示参数数组。根据参数组所表现出的适应度对种群进行选择、交叉、变异操作,直到满足终止条件,同时为了保留优质的个体,每次迭代所产生的最佳个体都会保留至下一代。遗传算法不依赖于问题的种类,它是一个应用框架[11]。遗传算法具有高效、并行、全局搜索等特点,能够在搜索过程中依据优胜劣汰原则,随机进行信息交换,自动获取并积累空间知识,求得最优解[12]。
对于本文所使用的SVR模型,需要进行编码寻优的参数变量有3个,分别为惩罚函数C、不敏感损失函数ε以及核函数系数σ。其中不敏感函数决定了支持向量选择的宽度,当算法中ε的数值过大时会导致宽度狭窄,使得模型的精度不能达到要求;而当ε的数值过小时会导致支持向量的数目过多,导致模型过于复杂。C决定着函数对于样本中离群点的选择问题,决定着函数的拟合程度,当C过大时函数的拟合程度得到了提高,但会使得泛化能力变差。而核函数函数系数的选取则影响着训练样本的分布和范围,个体的适应度计算方式为平均绝对误差。遗传算法寻优过程如下:
1)种群初始化。遗传算法的编码形式模拟自然界中生物体的碱对编码,常用的编码方式较多,可分为二进制编码、浮点编码和符号编码三大类[13]。本文采用二进制形式进行编码,即使用由0、1组成的二进制数组对3项参数进行编码。每项参数由6个二进制数字代表,即每个参数组由18位二进制数代表。原始种群以随机生成的形式产生。
2)适应度计算。在遗传算法中,适应度是评价个体基因优劣的指标参数。本文所采用的适应度计算方法为见式(6)的平均误差法,平均误差越小的个体适应度越佳。将个体的基因型进行解码后映射为对应的参数值并代入SVR模型中进行训练,输出预测结果。式(6)中y和y*分别为预测值与实际值:
![]()
(6)
3)选择操作。此操作是通过来模拟生物进化过程中“优胜劣汰”的现象来对种群进行寻优。根据适应度的大小,较差的个体将会被淘汰,适应度较高的个体则会被保留至下一代。本文使用轮盘赌法进行选择操作,即模拟转盘旋转的过程,适应度越佳的个体被选中的几率越大。
4)交叉遗传。本操作是模拟自然界生物体进行繁殖,染色体交叉遗传的过程,该操作的目的是增加算法的全局搜索能力[10]。本文所采用的交叉方式是将选定的一对个体的随机一段数组进行交换,新生成的个体会加入到下一代种群中。
5)染色体变异。为了防止种群陷入局部最小值,同时也是为了增加种群的多样性,需要加入变异操作。本文所采用的方式是对二进制进行取反处理,即随机选定个体中0、1二进制数字进行取反。
使用遗传算法进行参数寻优的流程如图1所示。
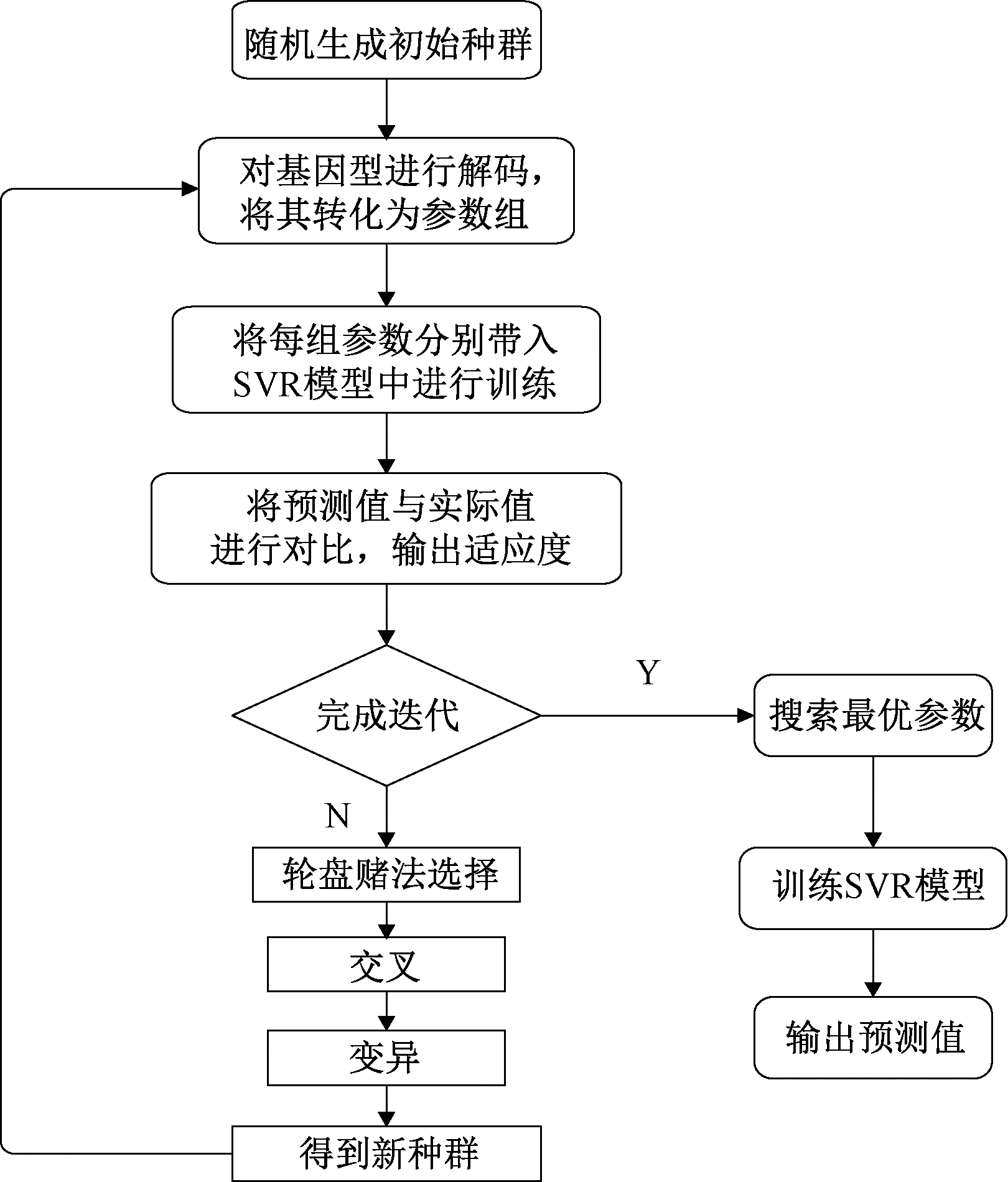
图1 遗传算法参数寻优流程
Figure 1 Genetic algorithm parameter optimization flow chart
2 实验验证及分析
本文所用于验证的数据集来源为北京市卢沟桥再生水厂进水处1年的相关水质数据,数据以天为单位,选取1个月的数据作为模型的验证数据集。
COD为化学需氧量,用来表示水体中需要被化学方法氧化的还原性污染物的量,常采用重铬酸钾作为氧化剂测量,其数值被称作CODCr,通常用COD表示。通过对数据集进行分析后发现数据集中BOD5的值与COD存在式(7)的耦合关系。郭泓利[14]等在对全国典型城市污水处理厂进水水质分析后也证明了BOD5与COD之间存在较好的线性拟合关系;李捷等[15]通过对昆明城市污水处理厂进水污水特征进行分析后,得到了COD、BOD5及SS在城市污水中相关性高且稳定的结论;陈丽琼等[16]通过对滇池水样进行分析后得出了pH对生化需氧量的测定有一定影响的结论,同时在BOD5的测定过程中氨氮会对测试结果产生一定影响[17]。本文决定使用COD、SS、pH和氨氮组成的四维输入数据作为SVR模型的输入变量。由于数据存在波动,对数据集进行了标准差标准化,将其转化为均值为0,方差为1的正态分布数据。设置初始种群的数量为500,由系统随机生。遗传算法寻优的迭代次数设置为200,种群杂交的概率和变异概率分别设置为0.6和0.01。
BOD5≈0.52COD
(7)
对于模型的优劣性评估本文采用了相对误差(RE)、平均误差(MAPE)以及均方根误差(RMSE)进行评价,见式(8)—(10)。
![]()
(8)
![]()
(9)
(10)
本文同时使用了GA-SVR模型、SVR模型和BP神经网络对1个月的连续时间内BOD5进行了预测,其中GA-SVR模型在迭代200次后,误差逐渐下降,实验所取得的最佳种群经过解码后得到的惩罚函数、不敏感损失函数以及核函数系数分别为1.7、0.058、0.024,使用这组参数对1个月连续时间的预测结果如图2a所示。为了对比,选取了3项参数分别为2、0.1、0.1的SVR常用参数进行实验,预测结果如图2b所示。为了进行验证结果,选取最为典型的BP人工神经网络进行对比实验,所选取的BP网络为泛化最好的三层结构网络,实验结果如图2c所示。实验所用数据来源均为北京卢沟桥再生水厂的进水数据。
取实验结果中的前10组输出BOD5数值进行对比(表1),模型的输入参数见表2。3种模型的评价指标参数如表3所示。
由表3可知,相对于BP神经网络及SVR模型,使用GA优化SVR的模型进行预测的结果更优,与SVR模型相比,使用GA-SVR模型BOD5预测值的平均误差降低了0.013,均方根误差由21.22 mg/L降低至16.88 mg/L。对于BP神经网络的平均误差更是降低了0.05,均方根误差则由28.26 mg/L降低至16.88 mg/L。可见,GA-SVR模型在BOD5的预测方面优于常规SVR模型及BP神经网络模型,且具有较高的实用性。

——BOD5预测值; ---BOD5实测值。
图2 不同模型的BOD5预测值与实际值的对比
Figure 2 Comparison of predicted and actual values of BOD5 in different models
表1 GA-SVR模型、SVR模型、BP神经网络输出的对比
Table 1 Comparison of GA-SVR model、SVR model and BP neural network output mg/L
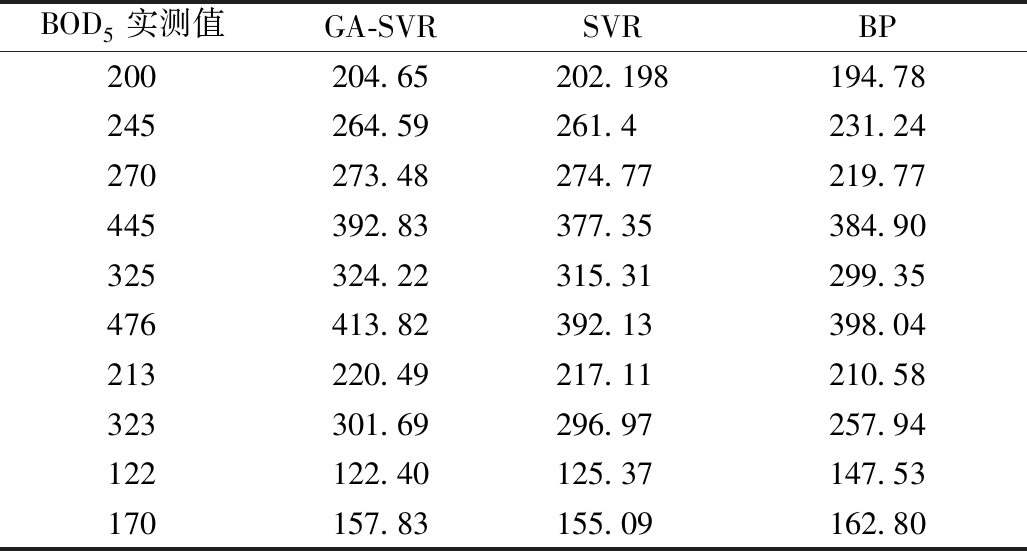
BOD5实测值GA-SVRSVRBP200204.65202.198194.78245264.59261.4231.24270273.48274.77219.77445392.83377.35384.90325324.22315.31299.35476413.82392.13398.04213220.49217.11210.58323301.69296.97257.94122122.40125.37147.53170157.83155.09162.80
3 结 论
针对现阶段水质参数BOD5难以实现在线测量的特点,设计并实现了一种基于遗传算法改进支持向量回归的预测算法,通过将遗传算法应用在SVR模型优化中,减少了选择参数的时间,提高了准确率。
表2 模型输入参数
Table 2 Model input parameters
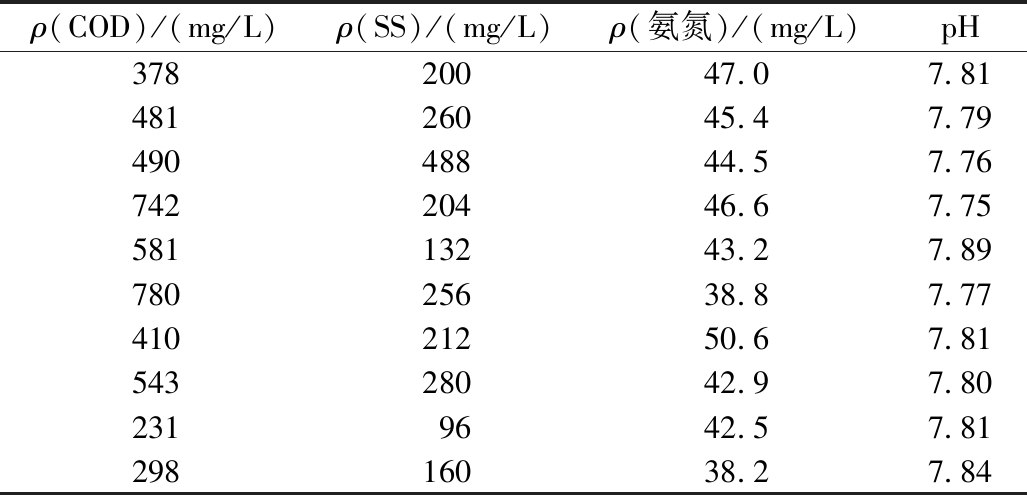
ρ(COD)/(mg/L)ρ(SS)/(mg/L)ρ(氨氮)/(mg/L)pH37820047.07.8148126045.47.7949048844.57.7674220446.67.7558113243.27.8978025638.87.7741021250.67.8154328042.97.802319642.57.8129816038.27.84
表3 三种模型的评价参数对比
Table 3 Comparison of evaluation parameters of the three models
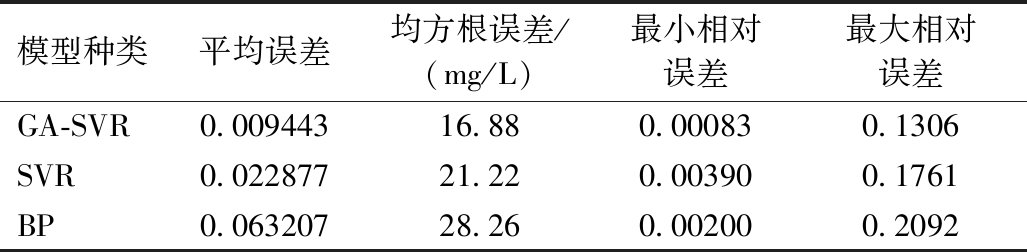
模型种类平均误差均方根误差/(mg/L)最小相对误差最大相对误差GA-SVR0.00944316.88 0.000830.1306SVR0.02287721.22 0.003900.1761BP0.06320728.26 0.002000.2092
经过实验,使用GA-SVR模型对BOD5进行预测的平均误差为0.009,均方根误差为16.88 mg/L,证明了GA-SVR水质预测模型的准确性与实用性。
本方法将机器学习技术应用在了水质预测监测领域,降低了对于BOD5的预测成本,实现了BOD5的在线测量。且GA-SVR模型具有较高的泛用性,对于水体水质管理方面的类似问题有一定的应用价值。
[1] LEWIS W M, WURTSBAUGH W A, PAERL H W. Rationale for Control of anthropogenic nitrogen and phosphorus to reduce eutrophication of inland waters[J]. Environmental Science & Technology, 2011, 45(24):10300-10305.
[2] 郑利杰, 高红杰, 宋永会, 等. 我国典型城市地表水水质综合评价与分析[J]. 环境工程技术学报, 2016(3):252-258.
[3] 刘长宇, 董绍俊. 水质生化需氧量快速检测新方法研究进展:现场、实时和就地监测[J]. 中国科学:化学, 2018, 48(8):194-201.
[4] 乔俊飞, 李瑞祥,柴伟,等.基于PSO-ESN神经网络的污水BOD预测[J]. 控制工程, 2016, 23(4):463-467.
[5] Predictive modeling for wastewater applications: linear and nonlinear approaches[J].Environmental Modeling&Software,2009,24(1):96-106.
[6] MIRBAGHERI S A, BAGHERI M, BOUDAGHPOUR S, et al. Performance evaluation and modeling of a submerged membrane bioreactor treating combined municipal and industrial wastewater using radial basis function artificial neural networks[J]. Journal of Environmental Health Science & Engineering, 2015, 13(1): 1-15.
[7] 王树东, 葛珉昊, 陈明明. 基于混合递阶遗传算法优化RBF神经网络的BOD5软测量方法[J]. 给水排水, 2014, 40(3): 149-153.
[8] 唐晓彬, 张瑞, 刘立新. 基于蝙蝠算法SVR模型的北京市二手房价预测研究[J]. 统计研究, 2018, 35(11):73-83.
[9] 墨蒙, 赵龙章, 龚嫒雯, 等. 基于遗传算法优化的BP神经网络研究应用[J].现代电子技术,2018,512(9):49-52.
[10] VAPNIK V.The Nature of Statistical Learning Theory [M]. Heidelberg: Springer, 1995.
[11] 周丽芳,文佳黎.基于遗传算法的虚拟足球游戏设计[J].计算机应用与软件,2017,34(2):209-213.
[12] 段青玲,张磊,魏芳芳,等. 基于时间序列GA-SVR的水产品价格预测模型及验证[J].农业工程学报, 2017(1):308-314.
[13] 任金霞,刘敏. 基于改进GA的云计算任务调度策略[J]. 沈阳工业大学学报, 2019, 41(3):320-325.
[14] 郭泓利,李鑫玮,任钦毅,等. 全国典型城市污水处理厂进水水质特征分析[J].给水排水,2018,54(6):12-15.
[15] 李捷, 王宏利, 隋军. 昆明某城市污水处理厂进水特征分析[J]. 给水排水, 2015(增刊1): 66-69.
[16] 陈丽琼, 茹婉红, 胡勇, 等. 生化需氧量测定方法的研究进展及现状[J]. 绿色科技, 2013(2): 138-141.
[17] 江梅, 范云慧, 瑞凤霞. 五日生化需氧量(BOD5)测定时防止氨氮干扰的方法探讨[J]. 净水技术, 2010, 29(6):62-65.