0 引 言
透水铺装作为雨水源头减排系统的重要技术之一,具有削减雨水径流、补充地下水以及降低径流污染负荷等作用。但透水铺装在寒冷地区受冻融的影响,易损程度显著增加,若处理不好就使寿命缩短,严重限制其使用范围。国内外已有学者开展了透水铺装冻胀损坏机理的研究,对透水铺装冻胀损坏程度的影响因素也开展了理论分析,以及提高其抗冻性能等方面的实验研究[1-6],但关于透水铺装面层孔隙率、水饱和度及透水基层厚度等因素对其抗冻性影响方面的实验数据支撑仍然缺乏。为此,笔者以透水砖铺装为例,针对上述3种影响因素对透水铺装防冻性能进行了实验研究,分析面层孔隙率、水饱和度、透水基层厚度对透水铺装面层抗冻性的影响,并对3种影响因素进行了相关性排序,以期对透水铺装在寒冷地区的应用提供科学技术支撑。
1 实验部分
1.1 实验材料
实验所用原材料包括:1)面层:不同材质、孔隙率的透水砖,规格为200 mm×100 mm×60 mm,主要物理性能见表1;2)找平层:粗砂;3)基层:透水级配碎石,将级配碎石过16 mm的集料筛;同时,为排除含泥量对透水基层渗透性能的影响,将碎石过0.075 mm的集料筛,筛除<0.075 mm的部分;4)其他:水泥、土工布、自来水、勾缝所用的粗砂。
表1 透水砖的主要物理性能指标
Table 1 Main physical performance indexes of the permeable bricks

粒径/mm孔隙率/%透水系数/(cm/s)初始抗压强度/MPa初始质量/(kg/块)1.91~9.515.3~25.42.13~2.3735.4~39.12.38~2.49
1.2 实验方案
根据GB/T 50082—2009《普通混凝土长期性能和耐久性实验方法标准》的快速冻融方法[7] ,并结合现有实验条件,每种实验条件下共有3组平行实验,对各组试件进行冻融实验并求其平均值。每次冻结时间为2~4 h,融化时间≥冻融时间的1/4;完全冻结后的温度为(-17±2) ℃,完全融化后的温度为(8±2) ℃。每间隔25个循环测透水砖质量和抗压强度,直到冻融循环次数达到200次或者透水砖质量减少5%后结束实验,其中,将每块透水砖在清水中浸泡1 d,使其完全饱和,然后通过调整试件静置时间来控制透水砖的水饱和度,以完成透水砖不同水饱和度的分级研究。透水砖铺装各层的结构厚度参考CJJ/T 188—2012《透水砖路面技术规程》[8],并结合目前施工时的常用做法和现有实验条件而定。不同条件下的透水砖铺装构造见表2—4,其中透水砖铺装的面层厚度均为60 mm,找平层厚度均为40 mm,透水基层厚度分别为100,150,200 mm。
表2 不同面层孔隙率条件下铺装结构
Table 2 Pavement structure under different brick porosity

实验编号孔隙率/%面层水饱和度/%面层厚度/mm找平层厚度/mm透水基层厚度/mm1-115.3完全饱和60402001-220.61-325.4
注:1)面层水饱和度是指面层中水占孔隙体积的百分比;2)空白部分与上一致。(下同)
表3 不同面层水饱和度条件下铺装结构
Table 3 Pavement structure under different brick saturation
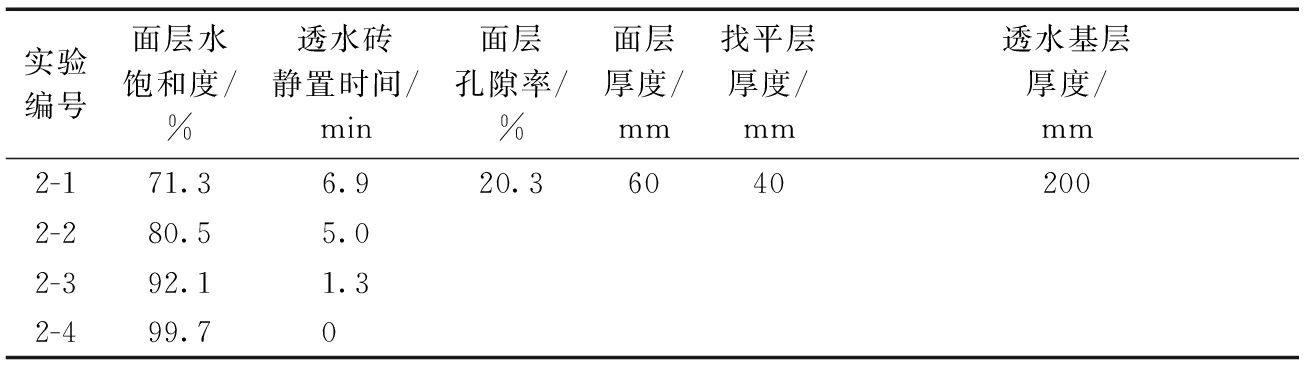
实验编号面层水饱和度/%透水砖静置时间/min面层孔隙率/%面层厚度/mm找平层厚度/mm透水基层厚度/mm2-171.36.920.360402002-280.55.02-392.11.32-499.70
表4 不同透水基层厚度条件下铺装结构
Table 4 Pavement structure under different base layer thickness
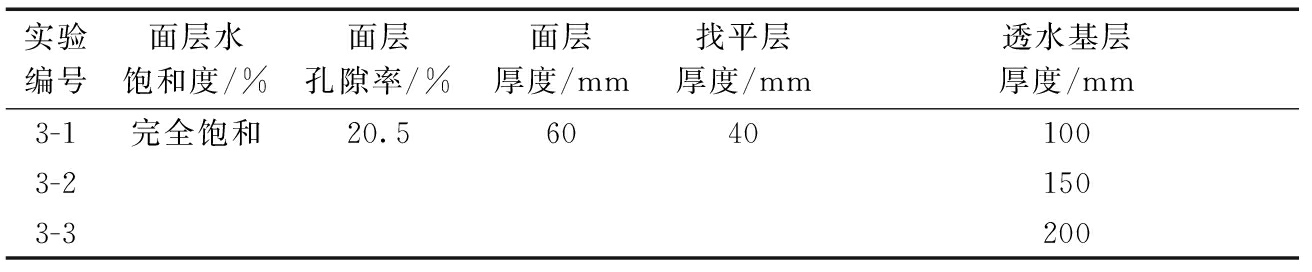
实验编号面层水饱和度/%面层孔隙率/%面层厚度/mm找平层厚度/mm透水基层厚度/mm3-1完全饱和20.560401003-21503-3200
整个实验装置置于尺寸为460 mm×460 mm×400 mm,厚度为5 mm的钢质实验箱内,见图1。每个实验箱内铺设8块透水砖,多组同步进行,按照标准养护条件养护到规定龄期28 d后,测各项初始值,因实验装置体积较大、实验组数较多,选用冷库进行冷冻,以达到冻融实验要求。实验用水为自来水。
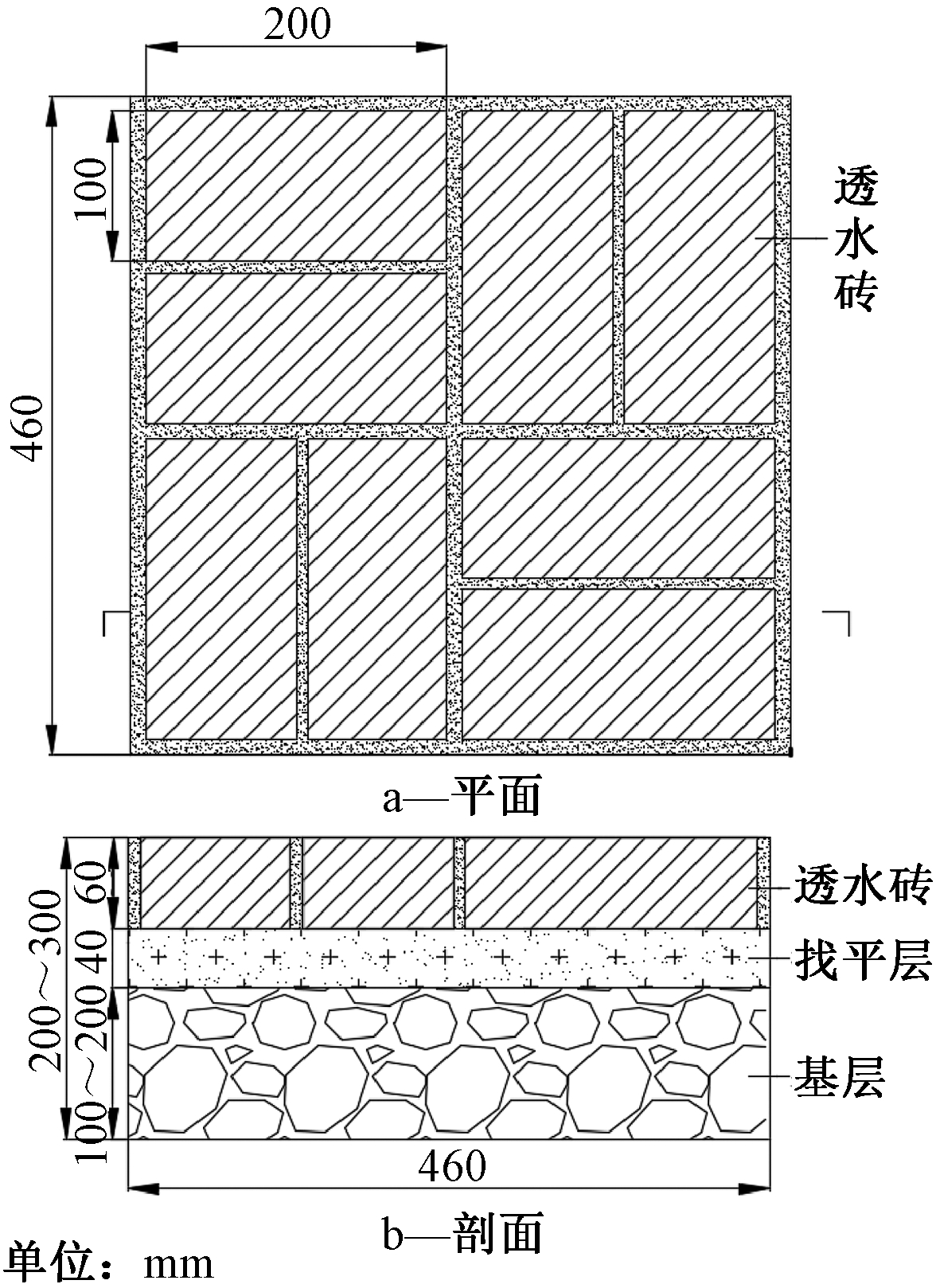
图1 实验装置构造示意
Figure 1 Sructure of the experimental device
1.3 抗冻性指标的计算方法
1.3.1 质量损失率
每25次冻融实验后,取出3块透水砖试件将其烘干,测其烘干后的质量,记为Mn(n为冻融实验次数),依次得到不同冻融循环次数下,不同面层孔隙率、水饱和度、透水基层厚度透水砖试件的质量,并取其平均值。透水砖质量损失率按式(1)计算:
![]()
(1)
式中:α为透水砖n次冻融循坏前后的质量损失率,%;M0为透水砖质量初始值,kg;Mn为透水砖n次冻融循环后的质量,kg。
1.3.2 抗压强度损失率
每次冻融实验结束后将其中3块透水砖试件放置在压力机上、下承压板正中,按照实验规定的6~10 kN/s的速度连续均匀加荷载直至试件被破坏,得到不同冻融循环次数下不同孔隙率和水饱和度透水砖试件的抗压强度Pn(n为冻融次数)的平均值。其抗压强度损失率按式(2)计算:
![]()
(2)
式中:β为透水砖抗压强度损失率,%;P0为透水砖抗压强度初始值,Pa;Pn为透水砖n次冻融循环实验后的抗压强度,MPa;其中![]() 为压力机测得压力值,N,A为透水砖受力面积,m2。
为压力机测得压力值,N,A为透水砖受力面积,m2。
2 实验结果及分析
2.1 透水砖铺装面层孔隙率与抗冻性的关系
根据实验数据和式(1)、(2)计算在25,50,75,100,…,200次冻融实验后的质量值、抗压强度值及损失率,变化规律如图2所示。
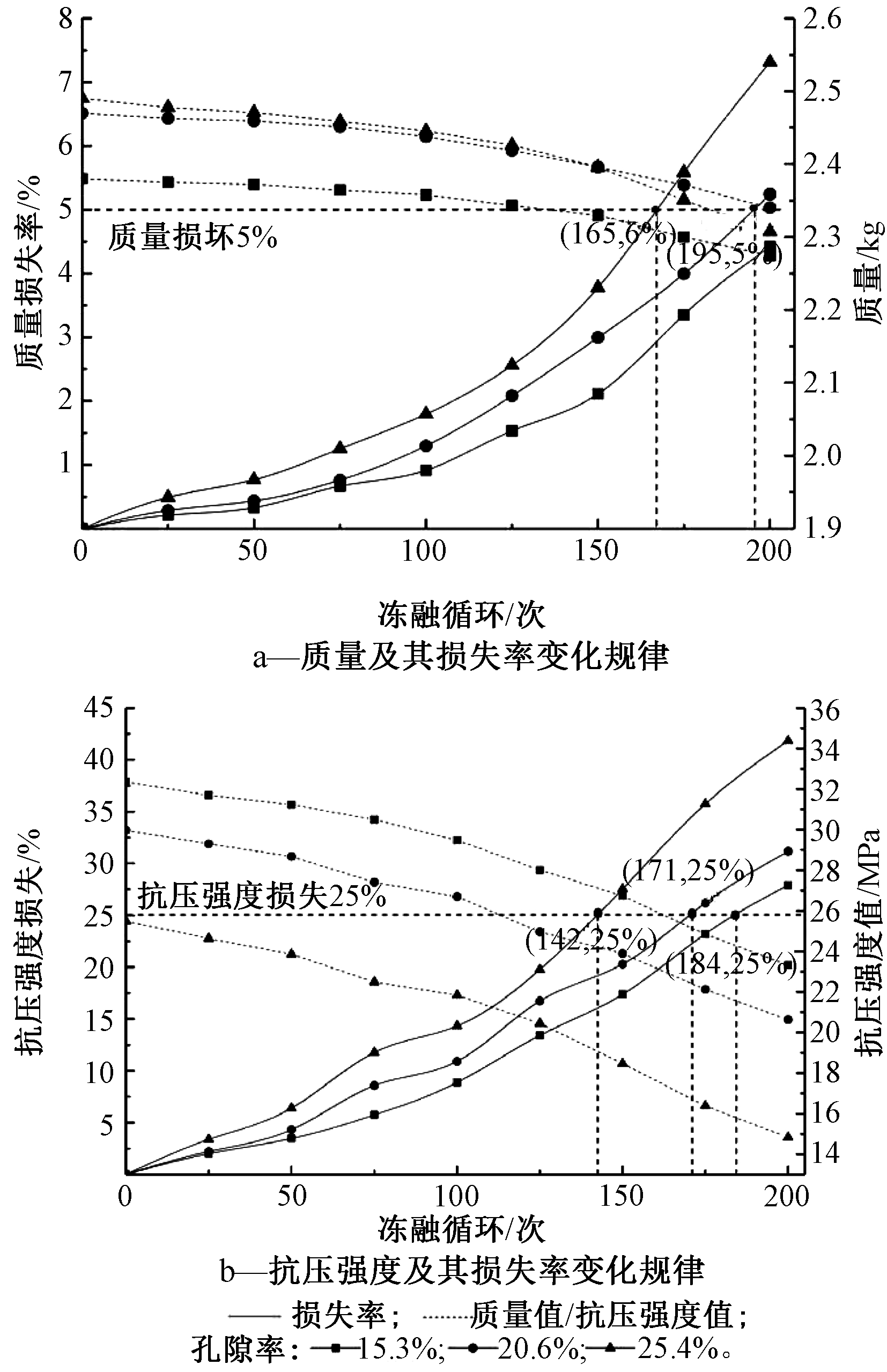
图2 不同面层孔隙率对其抗冻性的影响
Figure 2 The effect of porosity in different surface layer on frost resistance
由图2a可知:透水砖孔隙率为15.3%、20.6%、25.4%的质量初始值分别为2.38,2.47,2.49 kg。当冻融循环为25次时,3种不同孔隙率的透水砖质量损失均较小,相应的质量损失率分别为0.21%、0.28%、0.50%。随着冻融循环次数的增加,透水砖质量损失率逐渐增大,当冻融循环达到150次时,对应的质量损失率分别为2.11%、3.00%、3.77%;当冻融循环达到200次时,对应的质量损失率分别为4.42%、5.24%、7.31%;三者对应的透水砖质量损失依次加快,后两者损失率为5%的临界冻融循环次数依次为195,165次;而孔隙率为15.3%的透水砖质量损失值最小,损失率均低于5%。上述分析表明,透水砖冻融后的质量损失率随着冻融次数的增加而逐渐增大,其原因是随着冻融循环次数的增加,其内部水泥与粗、细骨料之间的孔隙逐渐增大,进而造成表面骨料剥蚀量增加且孔隙率大的剥蚀最为严重。在相同冻融次数下,孔隙率越大其质量损失量越大,原因是孔隙率越大,滞蓄在孔隙中的水量越多,其产生的冻胀应力随之增加,从而造成透水砖剥蚀量较大。
由图2b可知:透水砖孔隙率为15.3%、20.6%、25.4%的抗压强度初始值分别为32.35,29.97,25.49 MPa。当冻融循环为25次时,不同孔隙率条件下透水砖抗压强度损失值均较小,孔隙率为15.3%、20.6%、25.4%的抗压强度损失率分别为2.01%、2.22%、3.37%。随着冻融循环次数的增加,透水砖抗压强度损失率逐渐增大,当冻融循环达到150次时,对应的抗压强度损失率分别为17.37%、20.28%、27.54%;当冻融循环达到200次时,对应的抗压强度损失率分别为27.91%、31.17%、41.84%。3种孔隙率的透水砖抗压强度损失依次加快,损失率为25%的临界冻融循环次数分别为184,171,142。通过上述分析可知,随着冻融循环次数的增加,不同孔隙率的透水砖铺装面层的抗压强度损失量均增大;透水砖铺装面层抗压强度损失率与孔隙率有关,孔隙率越大,其抗压强度损失率越大,表明孔隙率与透水砖铺装面层抗压强度损失量呈负相关。根据冻胀损坏机理[9]并结合实验数据分析,这是由于不同孔隙率的透水砖在受到的冰负荷作用下,其内部体现出不同的结构稳定性,孔隙率大的透水砖在冻胀作用下产生了更大的孔隙,降低了骨料之间的黏合力,结构稳定性破坏较为严重,从而导致其抗压强度损失较大。
综上所述,孔隙率是影响透水铺装面层冻胀损坏程度的主要因素之一,因此,寒冷地区在使用透水铺装时,在保证其满足透水铺装的承载能力、渗透能力和滞蓄能力设计后[10],应尽量选择孔隙率较小的面层透水砖,以降低因冬季冻融造成的冻胀损坏。当然,渗透体积控制对面层孔隙率的要求和防冻性能对面层孔隙率的要求是一对矛盾,应根据当地冻土条件、冬季冻融次数、降雨数据等气候因素,结合质量和抗压强度的临界值以及拟定的抗冻等级科学选定其孔隙率。
2.2 透水砖铺装面层水饱和度与抗冻性的关系
根据实验数据和式(1)、(2)计算在25,50,75,100,…,200次冻融实验后不同面层水饱和度条件下的质量值、抗压强度值及损失率,变化规律如图3所示。
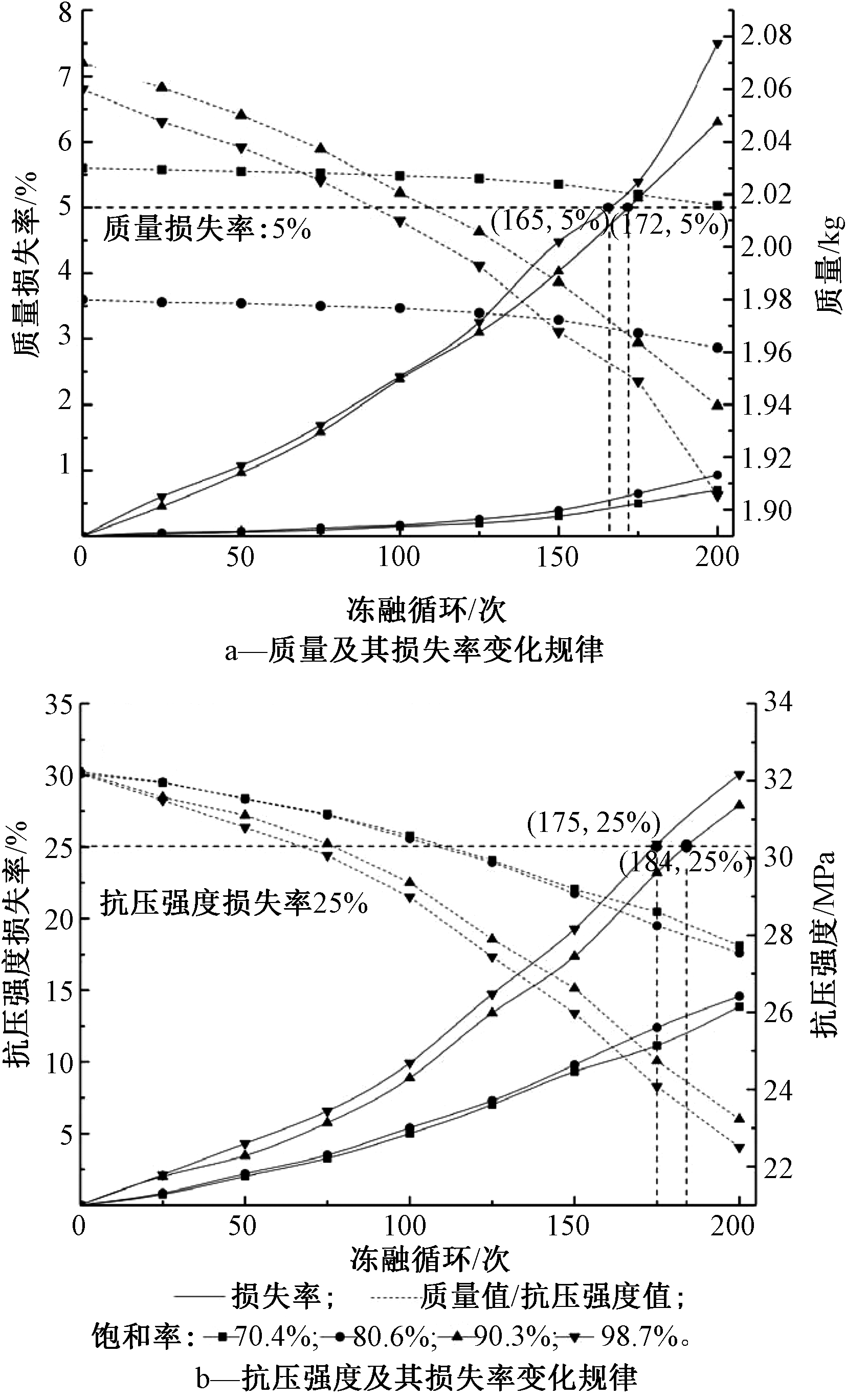
图3 不同面层水饱和度对其抗冻性的影响
Figure 3 The effect of different surface water saturation on frost resistance
由图3a可知:透水砖在水饱和度为70.4%、80.6%、90.3%、98.7%时,质量初始值分别为2.03,1.98,2.07,2.06 kg;当冻融循环为25次时,不同面层水饱和度条件下透水砖质量损失较小,水饱和度为70.4%、80.6%、90.3%、98.7%的透水砖对应的质量损失率分别为0.03%、0.05%、0.45%、0.6%;随着冻融循环次数的增加,透水砖的质量损失逐渐增大,同时面层水饱和度超过90%的透水砖质量损失增加程度明显高于面层水饱和度低于90%的透水砖。当冻融循环达到150次时,对应的质量损失率分别为0.30%、0.39%、4.03%、4.48%,当冻融循环达到200次时,对应的质量损失率分别为0.70%、0.93%、6.28%、7.54%;其中面层水饱和度为90.3%、98.7%透水砖质量损失最快,损失率为5%的临界冻融循环次数分别为172,165次;面层水饱和度为70.4%、80.6%的透水砖质量损失最小,损失率均低于5%。上述数据表明,当透水砖铺装面层水饱和度>90%时,质量损失超过水饱和度<90%的质量损失,证明超过90%的面层水饱和度的透水砖铺装其面层粗骨料剥蚀较严重,可作为透水砖铺装产生冻胀损坏的临界值。
由图3b可知:面层水饱和度为70.4%、80.6%、90.3%、98.7%的条件下,其透水砖抗压强度初始值分别为32.19,32.24,32.22,32.18 MPa。当冻融循环为25次时,不同面层水饱和度透水砖的抗压强度损失值均较小,面层水饱和度为70.4%、80.6%、90.3%、98.7%的抗压强度损失率分别为0.75%、0.84%、2.0%、2.12%;随着冻融循环次数的增加,不同面层水饱和度的透水砖抗压强度损失率均逐渐增大,当冻融循环达到150次时,对应的抗压强度损失率分别为9.32%、9.80%、17.37%、19.28%;当冻融循环达到200次时,对应的抗压强度损失率分别为13.87%、14.58%、27.91%、30.07%;其后两者的透水砖抗压强度损失最快,损失率为25%的临界冻融循环次数分别为184,175次;而前两者的透水砖抗压强度损失最小,损失率均<25%。综上所述,随着冻融循环次数的增加,不同水饱和度的透水砖铺装面层的抗压强度损失量均增大;当透水砖铺装面层水饱和度>90%,其抗压强度损失值远超过其水饱和度<90%时。其原因是在冻融循环的作用下,滞蓄在孔隙中的径流破坏了透水砖宏观的孔隙结构,且其系不可逆过程,面层水饱和度>90%的条件下,水结冰时膨胀量较大且无膨胀空间,造成其内部结构粗骨料之间的黏合力衰减量较多,从而导致其抗压强度损失较大。
综上所述,透水铺装是否发生冻胀损坏与其面层水饱和度有关,这与Sutter[11]、Leech[12]等研究学者提出的混凝土在饱和时易发生冻胀现象一致。透水铺装面层水饱和度>90%时,其结构和性能变化较大,这与水结冰过程中的产生冻胀系数大小有关。
2.3 透水砖铺装基层厚度与面层抗冻性的关系
根据实验数据和式(1)和(2)计算在25,50,75,100,…,200次冻融实验后不同透水基层厚度条件下的质量值、抗压强度值及损失率,变化规律如图4所示。
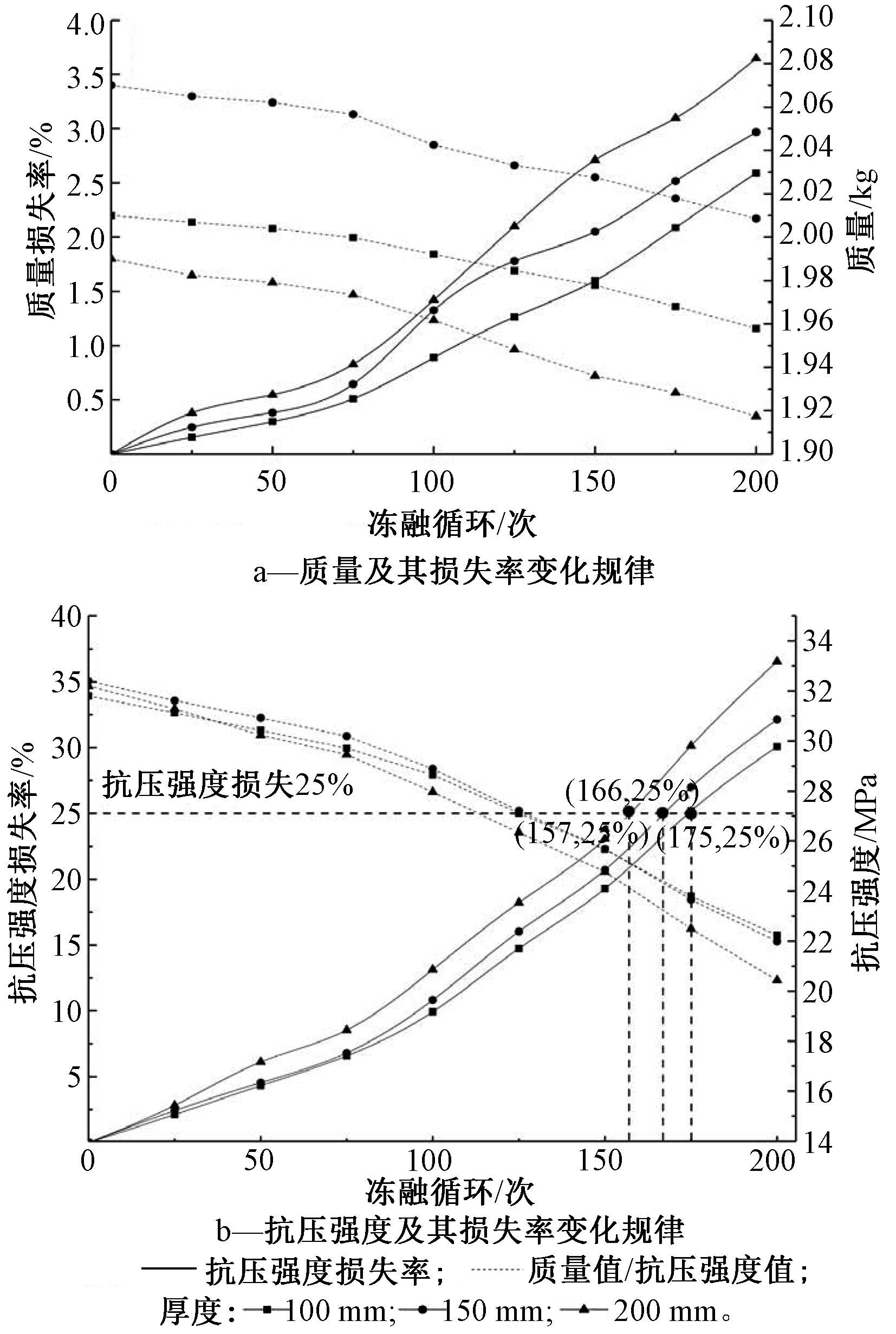
图4 不同透水基层厚度对面层抗冻性的影响
Figure 4 The effect of different permeable base thickness on frost resistance of the surface
由图4a可知:透水基层厚度为100,150,200 mm所对应的透水砖质量初始值分别为2.01,2.07,1.99 kg;当冻融循环为25次时,不同透水基层厚度条件下的透水砖质量损失较小,其对应的透水砖质量损失率分别为0.15%、0.25%、0.38%;随着循环次数的增加,每组透水砖的质量损失值逐渐增大,当冻融循环达到150次时,对应的质量损失率分别为1.60%、2.05%、2.71%,当冻融循环达到200次时,对应的质量损失率分别为2.59%、2.97%、3.65%,均未超过5%。上述数据表明,随着透水基层厚度的增加,其面层质量损失逐渐增大,会降低面层抗冻性能。
由图4b可知:透水基层厚度为100,150,200 m的透水砖铺装,其面层透水砖抗压强度初始值分别为31.8,32.4,32.2 MPa。当冻融循环为25次时,不同透水基层条件下的透水砖抗压强度损失值较小,厚度为100,150,200 mm对应的透水砖抗压强度损失率分别为2.12%、2.42%、2.82%;随着冻融循环次数的增加,透水砖抗压强度损失率逐渐增大,当冻融循环达到150次时,对应的抗压强度损失率分别为19.28%、20.71%、23.06%;当冻融循环达到200次时,各透水基层厚度对应的抗压强度损失率分别为30.07%、32.13%、36.54%。厚度为100,150,200 mm的透水砖质量损失值依次增大,损失率为25%的临界冻融循环次数分别为175,166,157次。上述数据表明,透水基层厚度对透水砖铺装面层的抗压强度有微小影响,分析其主要原因是厚度大的透水基层会延长滞蓄在其孔隙中径流的排空时间,增加其面层水饱和度,使得冻胀量增大从而导致其抗压强度损失较大。
综上所述,透水基层厚度也是影响透水铺装面层抗冻性能的因素,为提高透水铺装面层的抗冻性,应在透水铺装的面层、基层等结构层底部铺设渗排板或渗排管,减小径流在其内部结构中的排空时间,进而提高其使用寿命。
2.4 透水砖铺装抗冻性的主要影响因子相关性分析
用SPSS中的方差分析法进行多变量相关性分析,对透水砖铺装面层抗冻性的3个主要因子:面层孔隙率、面层水饱和度、基层厚度进行相关性排列。结果表明,三者均与面层抗冻性呈负相关,相关系数分别为-0.702、-0.822、-0.152,前两者相关性较显著;而基层厚度与面层抗冻性相关性弱。由此得到影响透水铺装抗冻性的主要因子相关性排序为面层水饱和度>面层孔隙率>透水基层厚度;面层水饱和度是透水铺装冻胀损坏的最主要因素,且临界水饱和度值在90%左右。
3 结 论
1)随着透水砖铺装面层孔隙率的增加,透水砖铺装面层抗压强度逐渐减小,二者呈负相关。在相同冻融循环次数下,面层孔隙率越大,透水砖铺装面层质量损失、抗压强度损失越大,说明当孔隙率越大时,透水铺装抗冻性能越低,因此在设计透水铺装时,在满足承载能力、渗透能力和滞蓄能力后,应选择较小的面层孔隙率,以增加其使用寿命。
2)面层水饱和度是影响透水砖铺装冻胀损坏程度的决定性因素,且面层水饱和度越高其抗冻性能越差,二者呈负相关。当面层水饱和度>90%时,透水砖铺装的抗冻性能远差于面层水饱和度<90%的抗冻性能。
3)透水基层厚度也是透水砖铺装面层抗冻性能的影响因素,厚度增加会延长其排空时间,增加冻融循环次数从而造成抗冻性降低。因此,寒冷地区在设计透水砖铺装时,应尽量缩短其排空时间,以减少冻融循环次数,提高透水砖铺装的抗冻性能。
4)利用SPSS方差分析法进行影响因素相关性分析发现,影响透水砖铺装面层抗冻性的主要因子相关性排序为:面层水饱和度>面层孔隙率>透水基层厚度。
[1] LAI Y M, ZHANG S M, YU W B. A new structure to control frost boiling and frost heave of embankments in cold regions[J]. Cold Regions Science and Technology, 2012, 79/80: 53-66.
[2] VANCURA M, MACDONALD K, KHAZANOVICH L. Microscopic analysis of paste and aggregate distresses in pervious concrete in a wet, hard freeze climate[J]. Cement & Concrete Composites, 2011, 33(10):1080-1085.
[3] LI W, POUR-GHAZ M, CASTRO J, et al. Water absorption and critical degree of saturation relating to freeze-thaw damage in concrete pavement joints[J]. Journal of Materials in Civil Engineering, 2011, 24(3): 299-307.
[4] FAGERLUND G. The critical degree of saturation method of assessing the freeze/thaw resistance of concrete[J]. Materials and Structures, 1977, 10(4): 217-229.
[5] 马悦因. 多孔混凝土透水基层材料设计研究[D].武汉:武汉理工大学,2008.
[6] 薛冬杰, 谭文菁. 透水性生态混凝土的抗冻研究[J].山西建筑, 2015, 41(32):119-120.
[7] 中华人民共和国住房和城乡建设部. 普通混凝土长期性能和耐久性实验方法标准:GB/T 50082—2009[S].北京:中国建筑工业出版社,2009.
[8] 中华人民共和国住房和城乡建设部.透水砖路面技术规程:CJJ/T 188—2012[S].北京:中国建筑工业出版社,2012.
[9] LITVAN G G. Pore structure and frost susceptibility of building materials[J]. Res Pap, 1973:17-30.
[10] 李俊奇, 张哲, 王耀堂, 等. 透水铺装设计与维护管理的关键问题分析[J]. 给水排水, 2019,45(6):26-31.
[11] SUTTER L, VAN DAM T, PETERSON K R, et al. Long-term effects of magnesium chloride and other concentrated salt solutions on pavement and structural portland cement concrete[J]. Transportation Research Record Journal of the Transportation Research Board, 2006, 1979(1): 60-68.
[12] LEECH C, LOCKINGTON D, HOOTON R D, et al. Validation of Mualem’s conductivity model and prediction of saturated permeability from sorptivity[J]. ACI Materials Journal, 2008, 105(1): 44.