0 引 言
随着城市化进程的不断加快,建筑与小区不透水区域明显扩大,绿地减少,土壤硬化板结现象在高密度建筑区域较为严重,使得在较大降雨条件下雨水不能迅速流入周边绿地土壤自身消化,而需要通过路面雨水口和市政雨水管网排出,增大内涝风险。
土壤入渗能力、孔隙比、含水率等物理性质是影响城乡绿地雨水入渗和蓄积能力的重要因素[1,2],研究入渗过程及其影响因子,有助于评估和优化绿地海绵体对降雨径流的渗蓄功能。渗透性不仅受土壤本身物理性质的影响,还受制于许多外在因素的限制[3],诸如植物种植程度、人为干扰情况、前期降雨情况等。土壤的物理性质直接影响土壤的通气透水性能和蓄水抗旱[4]。丁海晶等[5]通过相关性分析发现,非毛孔孔隙度和土壤稳定入渗速率之间存在正相关,土壤容重和土壤稳定入渗速率之间存在负相关抛物线关系。石亚芳等[6]研究发现,人为干扰情况增大会延长坡面产流时间,土壤稳定入渗速率增加,径流系数和累计入渗量降低。已有研究主要集中在实测绿地土壤的理化性质[7,8],而应用数理统计分析方法建立土壤渗透性能内外部影响因素之间关系模型的研究还很少。以实测数据为基础,探讨土壤渗透性与降雨产流过程的影响关系,可为评估绿地土壤蓄积雨水能力及海绵城市建设的建模和下垫面优化设计提供参考。
1 研究方法
1.1 研究过程
本研究首先实测和对比3种功能区(居住区、文教区和商业区)绿地的土壤物理性质(含水率、容重、密度、孔隙比和入渗速率),结合现场调查的植被覆盖度和人为干扰情况2种影响土壤渗透性的外在因素,利用SPSS 18.0中的双变量相关性分析和因子分析探讨不同功能区绿地渗透性能内外部影响因素之间的关系。然后,将初始入渗速率作为因变量,建立多元线性回归模型,并采取霍顿模型对初始入渗速率和稳定入渗速率的关系进行参数模拟,拟合得到3种功能性绿地土壤渗透模型及入渗曲线。进而,结合运动波计算模型,计算雨量径流系数,以期建立土壤渗透性能和降雨产流之间的量化关系。最后,将根据实测数据得到的径流系数值,和实际工程中常用的综合径流系数计算方法及结果进行对比,分析不同计算方法对径流系数结果的影响,详见图1。
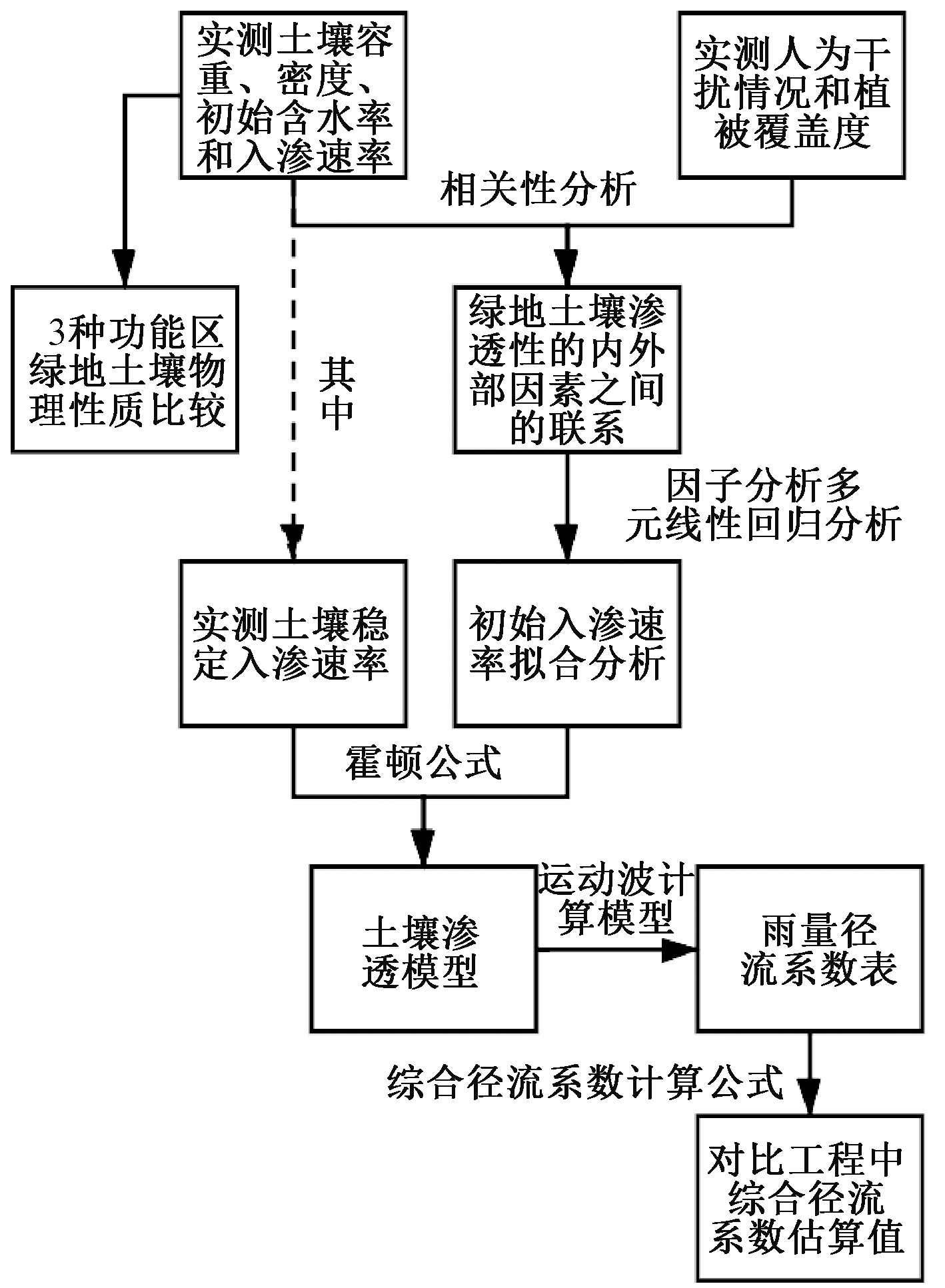
图1 研究过程
Figure 1 Process of the research
1.2 研究区域概况及试验测定
研究区域为北京市建成区。样品于2019年5、6月采集,在西城区、大兴区、通州区选取典型文教区、商业区和居住区,对场地内绿化带及宅间绿地进行布点和采样,共设21个采样点。采样时,根据绿地分布情况,选择有代表性的样点,尽量回避人工填充物,直接用环刀(体积100 cm3)取土,采样深度约为20 cm。
利用IN8-W型双环入渗仪(内环面积A=182.4 cm2)测定土壤稳定入渗率,每个样地重复3次,每次稳定时间约为60 min。以时间和入渗量为横纵轴,建立土壤入渗率关系曲线,以确定土壤的初始入渗率、稳定入渗率和衰减系数。土壤孔隙比一般无法直接测量,而是通过测定土壤的容重、密度计算所得,见式(1):
![]()
(1)
式中:P为土壤孔隙比,%;D为土壤容重,g/cm3;d为土壤密度,g/cm3。
土壤容重和初始含水率测定采用环刀法,土粒密度测定采用比重瓶法[9]。采集的土壤样品经烘箱105 ℃下8 h烘干后,将供试土壤碾碎,除去其中的碎石、人为侵入物、枯草及根系残留物等杂质,碾碎过1 mm筛称重,精确至0.001 g。
实验样点的植被覆盖度和人为干扰情况也通过现场测量获得,两者均采用面积加权法计算,即在采样点周围选取9个1 m×1 m的正方形区域,分区域考察植被覆盖比例、人为踩踏程度及植物倒伏等情况。
1.3 降雨数据
根据北京市地方标准DB 11/685—2013《雨水控制与利用工程设计规范》的暴雨强度公式,计算得出试验区不同重现期下降雨历时为1 h的降雨总量,见表1。
表1 北京不同重现期下降雨数据
Table 1 Rainfall with different return periods in Beijing

重现期/a设计暴雨强度q/[L/(s·100 m2)]1 h降雨量H/mm11.0035.8621.2444.6231.3849.7451.5656.19
1.4 理论计算与统计分析
运动波计算模型[10]见式(2):
![]()
(2)
式中:C为雨量径流系数;D1为透水区洼蓄量,mm;D2为不透水区洼蓄量,mm;I为不透水区面积比,%;m为系数,若不透水区域产生积水或地表径流,则m=1,否则m=0;n为系数,若C>0,则n=1,否则n=0;F为入渗量,mm,入渗量F为入渗曲线上t时间内曲线与横纵坐标轴包围的面积。
综合径流系数计算方法[11]见式(3):
Cv=(1-I)Cvp+ICvi
(3)
式中:Cv为综合径流系数;Cvp为透水区域径流系数; Cvi为不透水区域径流系数。
2 结果与讨论
2.1 城市建筑小区绿地土壤物理特性
2.1.1 土壤质地
北京城市绿地土壤多属砂质土[12],同时也有一定数量的垫土,生活废弃物、建筑垃圾等外部侵入体的影响使土壤质地变得更粗,土壤颗粒组成的差异较大,即便是同一种实验样地仍有很大差异,表明土壤性质空间变异性强[13]。由于研究区域内绿地环境均不相同,影响渗透能力的相关因素间均存在差异,因此采用现场测定的方法来分析,以提高准确性。
2.1.2 土壤孔隙比及初始含水率
实验结果显示,针对本研究范围内的绿地,居住区和商业区绿地由于压实和踩踏等人为活动的影响,表现为土壤容重增大、孔隙比降低、渗透性减弱现象。而文教区绿地受人为活动影响较少,土壤容重较小,孔隙比较高,表现为渗透性较好,见表2。这也说明土粒密度小,土壤比较疏松,孔隙所占百分数大,容重也就比较小;反之,土粒密度大,土体比较紧实,结构性差,孔隙少,容重也就比较大[14,15]。
表2 环刀实验实测数据
Table 2 Measured data of ring sampler experiment

功能区土壤容重/(g/cm3)土壤密度/(g/cm3)土壤孔隙比/%土壤初始含水率/%平均值标准偏差平均值标准偏差平均值标准偏差平均值标准偏差居住区1.490.132.750.1047.376.9711.011.33文教区1.200.112.530.0452.594.5310.480.84商业区1.340.052.750.0851.212.3110.700.86
2.1.3 土壤渗透性
实验结果表明,在本研究范围内的建筑小区绿地中,3种用地功能的绿地土壤入渗速率存在较大的差异,其中居住区绿地较为显著。初始入渗速率和稳定入渗速率排序为:居住区>文教区>商业区,原因可能是采样的居住区和部分文教区土壤多为人工回填土,而商业区土壤多为原始土,人工回填土渗透性能优于原始土。
实验样地的入渗速率见图2。可知均存在差异,原因有:1)样点测量日期的前日曾有降雨,土壤含水率较高,使初始入渗速率偏低;2)样点处地面下存在较为粗壮的植物根系,影响雨水的下渗量,入渗速率较低;3)人为干扰情况较大,土壤压实情况严重导致入渗速率较低[16];4)采样区域刚于近期完成相关改造,土壤较为疏松,土壤入渗速率偏高。采用各功能区平均渗透速率作图,如图3所示,土壤入渗曲线为平滑曲线,经SPSS拟合,发现曲线符合霍顿模型[17]。
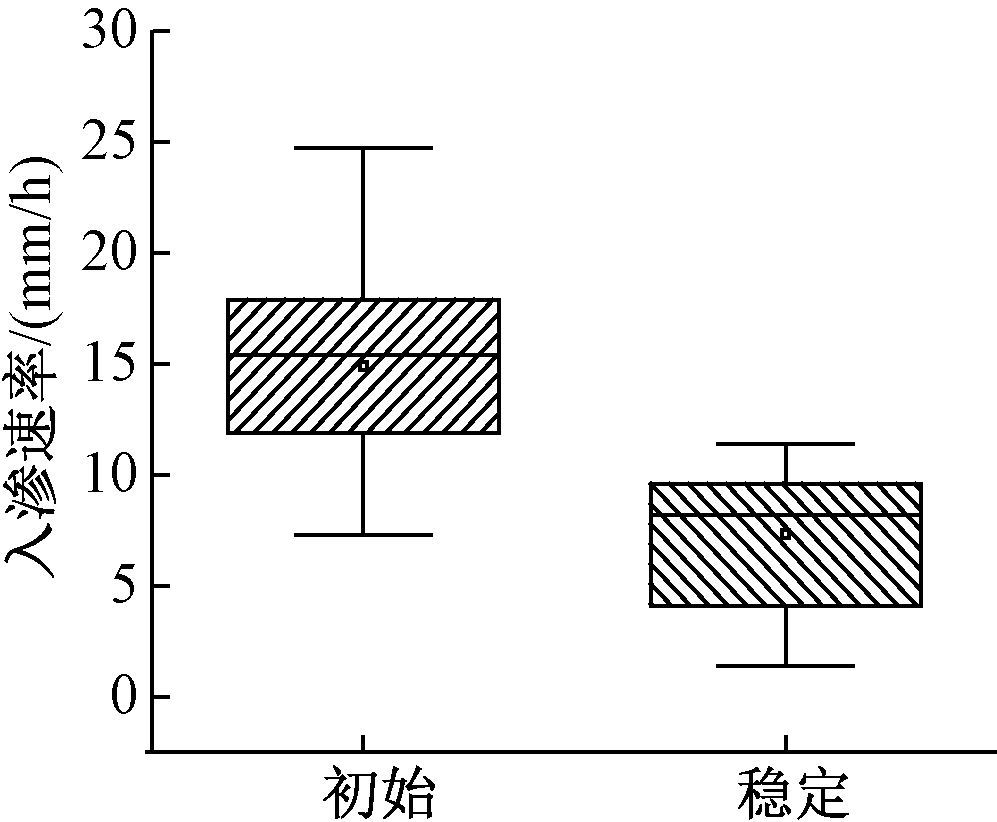
图2 实测入渗速率范围
Figure 2 Measured infiltration rates’ range
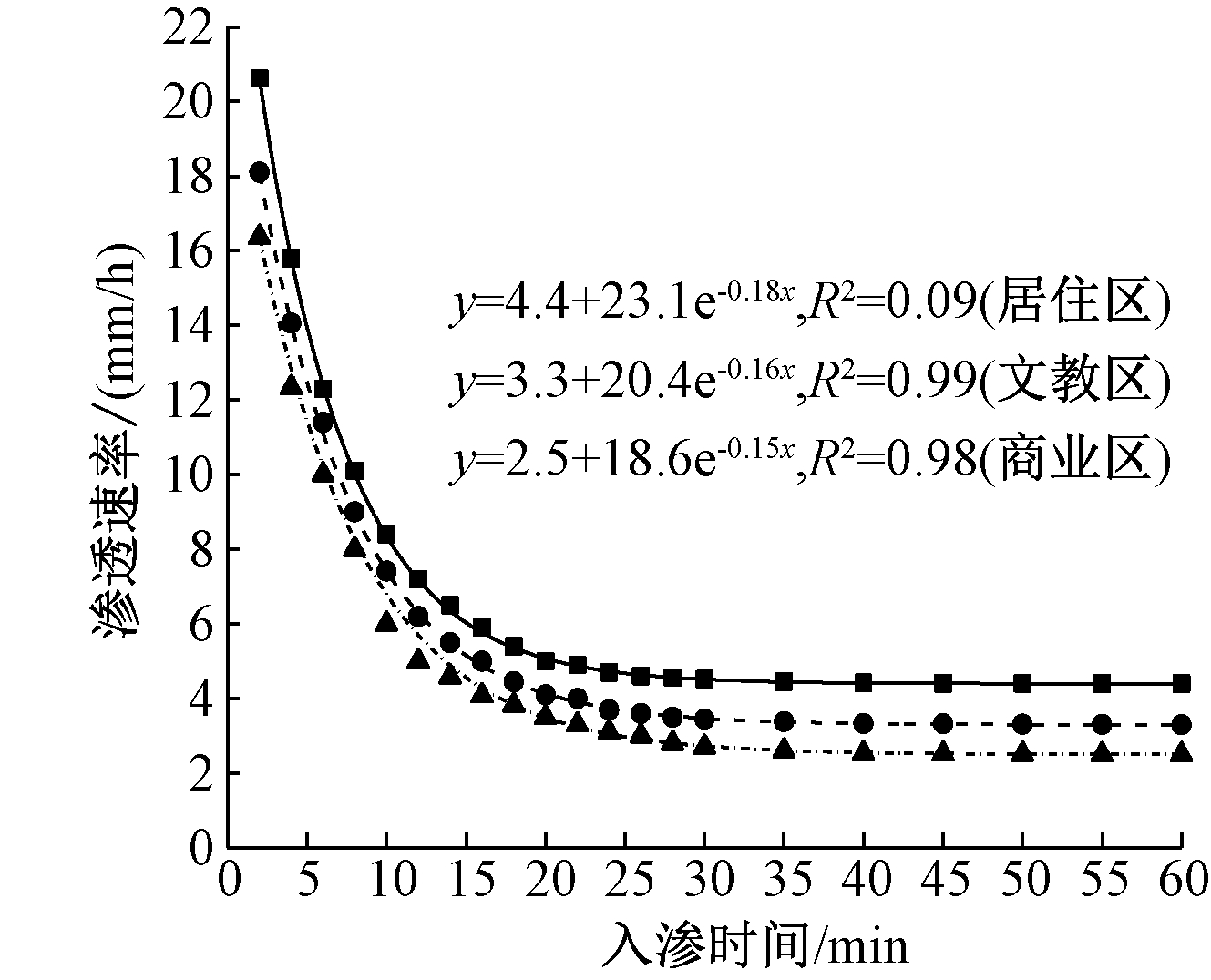
![]() 居住区;
居住区;![]() 文教区;
文教区;![]() 商业区。
商业区。
图3 3类功能区绿地土壤入渗曲线
Figure 3 Soil infiltration curves of green space in three types of functional areas
2.2 影响土壤渗透性能的相关因素分析
2.2.1 相关性分析
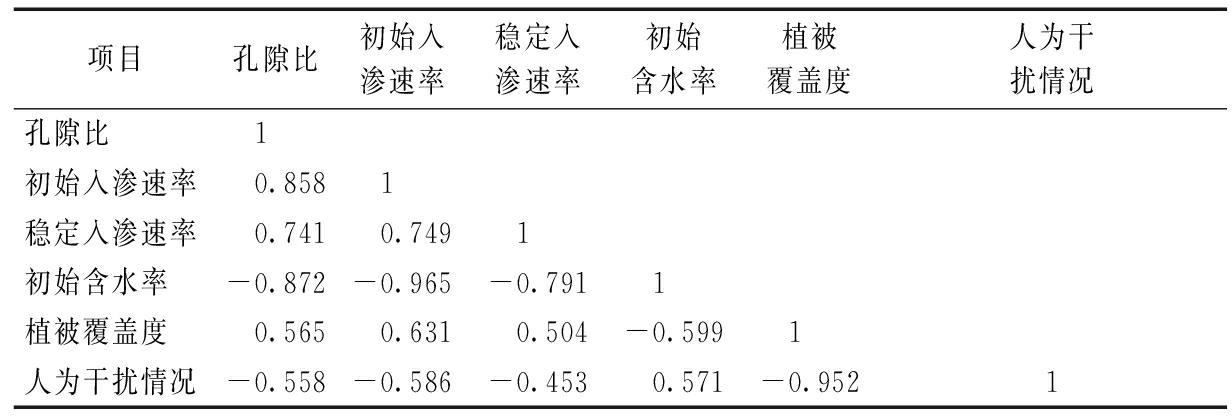
根据文献[5,17-19],影响土壤渗透性能的因素主要有土壤质地、土层深度、样地坡度、孔隙比、有机质、含水率、容重、人为扰动程度和植被覆盖类型等。其中,影响初始入渗速率的有孔隙比、土层深度变化、初始含水率和植被覆盖类型等,影响稳定入渗速率的有土壤密度、容重、初始含水率、人为踩踏干扰情况和初始入渗速率等因素。因此,选取孔隙比、初始含水率、植被覆盖度、人为干扰情况、初始入渗速率和稳定入渗速率6个已知指标,通过对6个指标的相关性分析,发现各指标之间存在着不同程度的相关关系,见表3。
表3 土壤物理性质相关性
Table 3 Correlation of soil physical properties
项目孔隙比初始入渗速率稳定入渗速率初始含水率植被覆盖度人为干扰情况孔隙比1 初始入渗速率0.8581 稳定入渗速率0.7410.7491 初始含水率-0.872-0.965-0.7911 植被覆盖度0.5650.6310.504-0.5991 人为干扰情况-0.558-0.586-0.4530.571-0.9521
由表3可知:孔隙比与初始入渗速率呈强正相关,与初始含水率呈强负相关;而初始含水率与初始入渗速率呈强负相关,说明孔隙比、初始含水率和初始入渗速率三者相互关系相当紧密。植被覆盖度与人为干扰情况呈强负相关,绘制散点图4。可知:两者关系呈显著线性负相关,植被覆盖度越高,人为干扰情况越小,土壤的渗透性能越好,主要原因是人为踩踏会造成土壤紧实,并可能会踩断绿化植物的茎,不利于其生长。
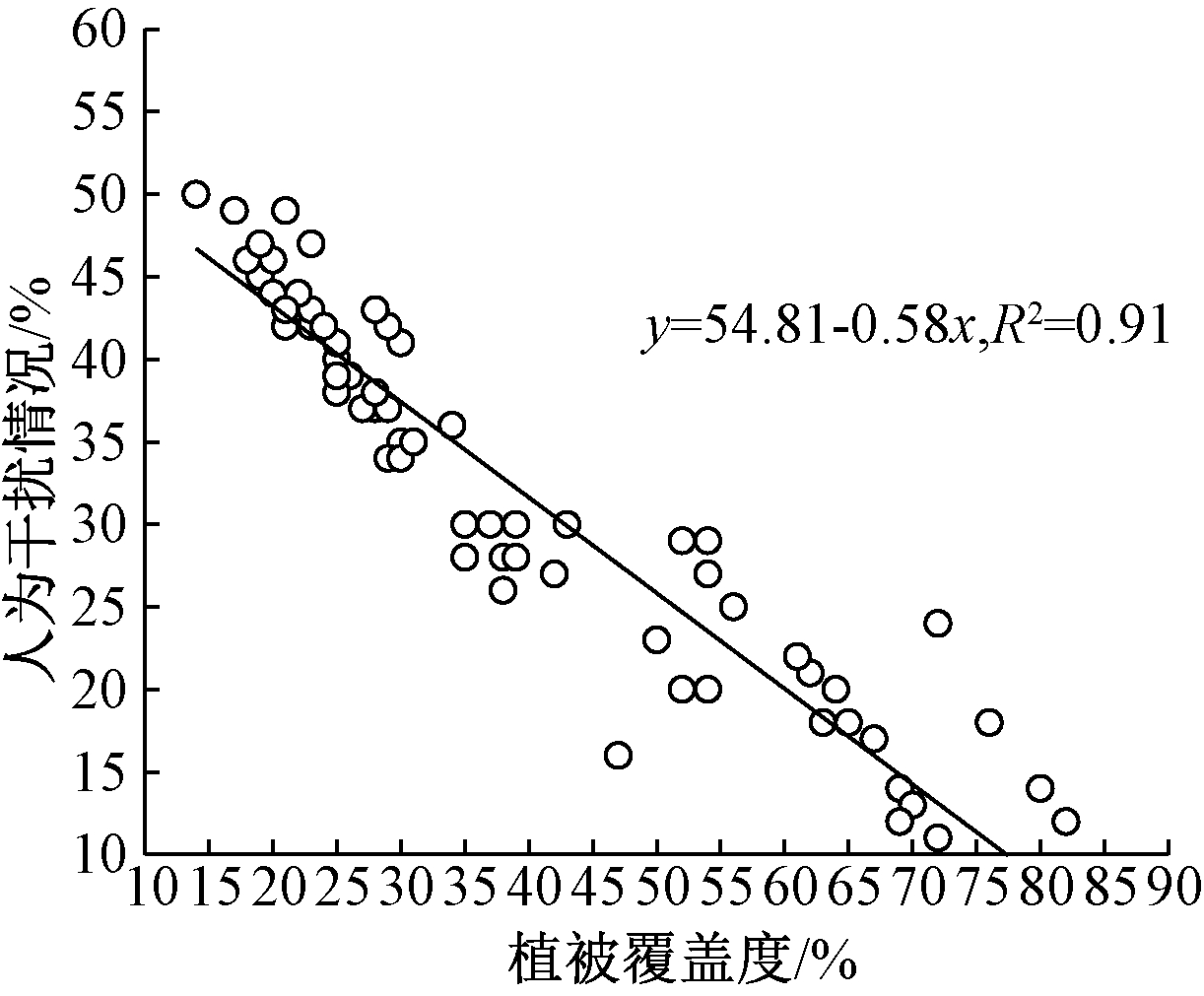
图4 人为干扰情况与植被覆盖度线性关系
Figure 4 Linear formula between human disturbance and vegetation coverage
2.2.2 因子分析
相关性分析是自变量两两之间的相互关系。受制于因子间的相互作用,相关系数并不能完全正确地反映它们之间的真正关系。因子分析是一种把多个变量化为少数几个综合变量的多变量分析方法,能够将有限个不可观测的隐变量用来解释原始变量之间的相关关系[20]。由表3可知:相关分析中各变量间表现出较好的相关性,这是进行因子分析的前提。针对初始土壤入渗率的相关影响研究,选取孔隙比、初始含水率、人为干扰情况和植被覆盖度4种因子,并对原始特征量进行了KMO和Bartlett检验,结果表明,KMO检验值为0.643>0.6,表明变量之间存在较强的偏相关性,而Bartlett检验显著值sig为0,表明变量之间无较强的独立性,因此此类特征适宜使用因子分析进行降维处理。
通常,提取特征值>1并且累积贡献率达到85%以上的成分作为默认的选取公共因子的标准。将指标数据标准化处理之后在SPSS 18.0中求出相关矩阵旋转前后的特征值和贡献率,见表4和表5。由表4可知:符合标准的为前2个成分,累积贡献率达到95.48%,可以反映原有指标的信息。
表4 实测北京地区初始入渗性能特征值和累积贡献率
Table 4 Measured initial infiltration performance characteristic values and cumulative contribution rates in Beijing

成分初始特征值提取载荷平方和旋转载荷平方和总计方差百分比/%累积贡献率/%总计方差百分比/%累积贡献率/%总计方差百分比/%累积贡献率/%13.0275.5075.503.0275.5075.501.9448.6248.6221.0821.0795.481.0821.0795.481.8746.8595.4830.133.3698.8440.051.16100.00
表5 旋转后的成分矩阵
Table 5 Components matrix after rotation

指标成分12孔隙比0.943初始含水率-0.938植被覆盖度-0.913人为干扰情况0.926
由表5可知:成分1包括孔隙比与初始含水率,两者大致互为相反数;成分2包括植被覆盖度与人为干扰情况,两者也大致互为相反数。因此,一个成分中可取一种因子作为代表。
2.2.3 初始入渗速率拟合分析
根据上述分析,分别选取成分1和成分2中的一种进行两两组合,均通过SPSS 18.0回归分析,经线性拟合得到初始含水率和植被覆盖度作为分析初始入渗速率的样本时,复相关系数最大,为0.97,调整后的R2为0.94,此时初始入渗速率的近似方程为:
y=4.695-0.031x1+0.001x2
(4)
式中:x1为初始含水率,%;x2为植被覆盖度,%。该方程通过显著性水平α=0.05的F检验。由VIF=1.56<<10可知,无多重共线性存在。经多元回归分析得到残差的直方图、正态P-P图和散点图显示,式(4)为最终方程。
从本研究实测数据出发,分析得到了初始入渗速率的拟合方程。但影响土壤初始入渗速率的因素还包括土壤有机质、前期降雨情况等因素,还需要深入研究,以得出更为精确的结果。
2.3 绿地土壤入渗能力对降雨产流的影响
综合式(3)、实测土壤数据和降雨数据(表1),计算出北京典型建筑小区实际的雨量径流系数,见表6。可知:各区入渗量不同对相同不透水比例下的径流系数影响不大,降雨量越大,不透水面积比例越大,影响越小。跟前期研究结果[21]对比可知,实测的1 h土壤入渗量大于单一土层的入渗量,故得出的径流系数偏小。这是由于实验样地的土壤多为回填土,回填土渗透性能优于单一砂质土;同时,实验样地上的植被根系会促进雨水的快速入渗,也会截留一定量的雨水。两方面均造成地表径流量减少。
表6 北京市不同功能区降雨1 h的雨量径流系数
Table 6 Runoff coefficients of 1 hour rainfall in different functional areas of Beijing
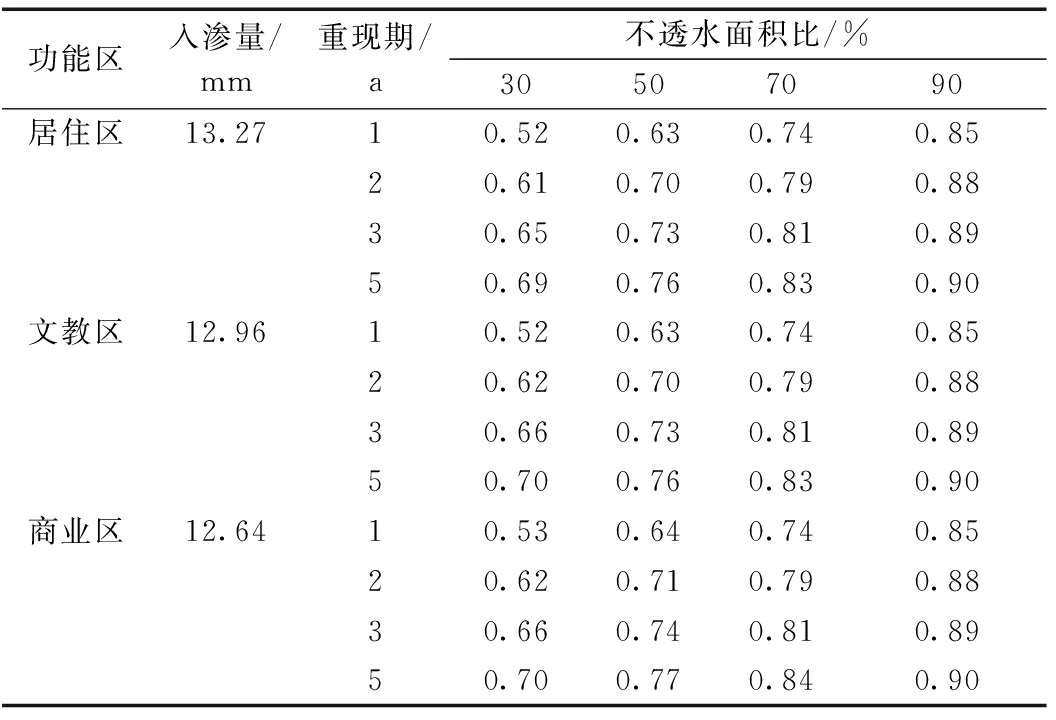
功能区入渗量/mm重现期/a不透水面积比/%30507090居住区13.2710.520.630.740.8520.610.700.790.8830.650.730.810.8950.690.760.830.90文教区12.9610.520.630.740.8520.620.700.790.8830.660.730.810.8950.700.760.830.90商业区12.6410.530.640.740.8520.620.710.790.8830.660.740.810.8950.700.770.840.90
北京年径流总量控制率为75%~85%对应的设计降雨量为22.8~33.6 mm[11],得到入渗量占年径流总量控制率条件下对应的设计降雨量比例见图5,两者比值和降雨量呈负相关,针对本研究范围内的实验样地,居住区的比值为39.5%~58.2%,文教区的比值为38.6%~56.8%,商业区的比值为37.6%~55.4%。
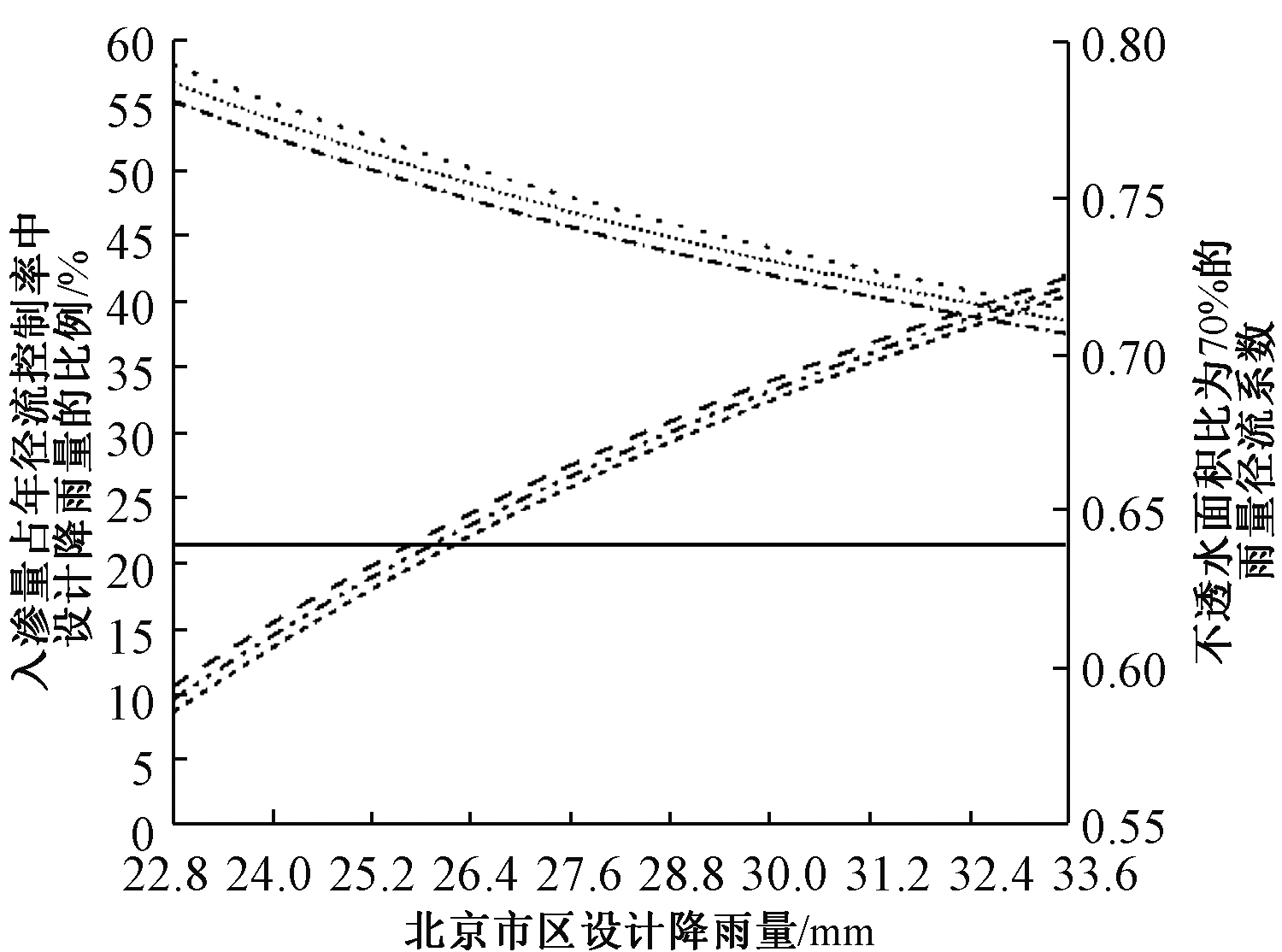
····居住区比例;……文教区比例; -·-·-·商业区比例; -----居住区径流系数; -··-文教区径流系数; --·商业区径流系数; ——经验值径流系数。
图5 年径流总量控制率在75%~85%下北京城区土壤入渗能力与径流的关系
Figure 5 Relationship between soil infiltration capacity and runoff in Beijing urban area under the annual rainfall volume capture ratio of 75%~85%
由于目前建筑与小区绿地率普遍在30%左右,故选取不透水面积比例I为70%时,代入式(3)得到的综合径流系数估算值Cv为0.64。由图5可知:3种功能区实际径流系数C为0.59~0.72,当降雨量<26 mm时,实际径流系数略低于经验值,其他情况均偏高。可能的原因是:透水区域经验值通常采用0.15进行计算,而针对本文的研究对象,透水区域径流系数为0.00~0.43。另外,随着降雨量的增大,实际值和经验值之间的差异逐渐增大,实际径流量高于工程设计的估算值,可能造成强降雨时的积水现象。因此,利用具有环境功能的城市绿地进行雨水调控时,需要根据降雨条件、土壤入渗情况等进行计算评估、设施选址,或改良原有土壤理化性质,使其达到入渗要求,才能充分发挥土壤的雨水调蓄作用。
3 结 论
1)土壤初始入渗速率和稳定入渗速率作为表现土壤渗透性能的重要组成因素,直接影响降雨入渗及径流过程。根据本研究实测数据,理论分析表明,土壤初始入渗速率主要与初始含水率(内因)和植被覆盖度(外因)有关,并建立初步关系式;稳渗速率主要与初始含水率和初始入渗速率有关;实验测定稳渗速率和初始入渗速率之间的关系符合霍顿公式拟合的入渗曲线,由此得到本研究范围内3种功能区绿地的土壤渗透模型,并确定了北京市典型建筑小区应用霍顿公式的主要参数,可为北京地区的SWMM模型参数选择等提供参考。
2)运用运动波计算模型,以北京地区实测数据建立的土壤渗透模型和数据为基础,获得了在不同功能区、小区不透水区域比例和降雨重现期下的径流系数表,以及入渗量占年径流总量控制率条件下对应的设计降雨量比例,定量描述了3种功能区实际径流系数与经验值的差值范围,并细化了透水区域径流系数的取值范围,可为快速评估土壤入渗能力和下垫面情况提供一定参考。
致谢:
感谢宋琪、马凌宇、覃信坤和相关人员对本研究做出的贡献。
[1] 朱永杰, 毕华兴, 霍云梅, 等. 北京地区下凹式绿地土壤渗透能力及蓄水对土壤物理性质的影响[J]. 中国水土保持科学, 2015, 13(1):106-110.
[2] 张金龙, 张志政. 下凹式绿地蓄渗能力及其影响因素分析[J]. 节水灌溉, 2012(1):44-47.
[3] 刘青柏, 刘明国, 王玉涛, 等. 不同林型立地土壤水分性状及其持水能力的比较[J]. 干旱区研究, 2011, 28(5):775-779.
[4] 王玲, 冯茂松, 洪志刚, 等. 兴文县香椿人工林土壤物理性质研究[J]. 土壤, 2014,46(3):512-517.
[5] 丁海晶, 姜姜, 张金池. 土壤渗透性的区域变化规律及因子分析[J]. 水土保持学报, 2019, 33(1):51-56.
[6] 石亚芳, 赵允格, 李晨辉, 等. 踩踏干扰对生物结皮土壤渗透性的影响[J]. 应用生态学报, 2017,28(10):3227-3234.
[7] 聂发辉, 李田, 姚海峰. 上海市城市绿地土壤特性及对雨洪削减效应的影响[J]. 环境污染与防治, 2008,30(2):49-52.
[8] 于冰沁, 车生泉, 严巍, 等. 上海城市现状绿地雨洪调蓄能力评估研究[J]. 中国园林, 2017,33(3):62-66.
[9] 车生泉, 于冰沁, 严巍. 海绵城市研究与应用:以上海城乡绿地建设为例[M]. 上海: 上海交通大学出版社, 2015.
[10] JAMES C Y G, URBONAS B. Volume-based runoff coefficients for urban catchments[J]. Journal of Irrigation and Drainage Engineering, 2014, 140(2):1-5.
[11] 中华人民共和国住房和城乡建设部. 海绵城市建设技术指南:低影响开发雨水系统构建(试行)[M]. 北京: 中国建筑工业出版社, 2015.
[12] 马秀梅.北京城市不同绿地类型土壤及大气环境研究[D]. 北京: 北京林业大学,2007.
[13] 邹明珠, 王艳春, 刘燕. 北京城市绿地土壤研究现状及问题[J]. 中国土壤与肥料, 2012(3):1-6.
[14] 包昱峰, 高甲荣, 高阳. 密云水库北京集水区典型植被土壤入渗特征研究[J]. 水土保持研究, 2007, 14(4):176-179.
[15] 赵景波, 陈颖, 曹军骥, 等. 青海湖西北部土壤入渗规律研究[J]. 陕西师范大学学报(自然科学版), 2011,39(3):90-96.
[16] 郭晓朦, 何丙辉, 秦伟, 等. 不同坡长条件扰动地表下土壤入渗与贮水特征[J]. 水土保持学报, 2015,29(2):198-203.
[17] 黄延林, 马学尼. 水文学[M]. 4版. 北京: 中国建筑工业出版社, 2011.
[18] 黄祺, 何丙辉, 秦伟, 等. 自然降雨条件下扰动地表土壤入渗性能变化特征[J]. 灌溉排水学报, 2015, 34(1):91-95.
[19] 陈三雄, 沈义. 黄浦江源头区主要植被类型土壤入渗特征及模拟分析[J]. 水土保持研究, 2016,23(6):59-63.
[20] 张一璇, 史常青, 杨浩, 等. 永定河流域官厅水库南岸典型林分土壤饱和导水率研究[J]. 生态学报, 2019, 39(18):1-8.
[21] 王思思, 王榕, 宫永伟, 等. 基于运动波计算模型的北京城市土壤渗透性对雨量径流系数的影响分析[J]. 环境工程, 2019, 37(7):25-29.