0 引 言
目前我国大多数城市,尤其是老城区的排水体制大都采用截流式合流制,合流制溢流(CSO)污染问题严重,雨水混合生活污水和工业废水通过管道溢流的方式排入河道水系,给水环境带来了极大的负面影响。近年来国内外对CSO污染控制的研究和实践不断深入,美国等国家较早将灰绿设施相结合的方法应用在CSO污染控制上,并取得了良好的效果[1,2],将源头控制、污染物扩散途径控制和终端治理三者结合起来,能取得较好的CSO预期治理效果[3,4]。随着我国逐渐推进海绵城市建设工作,合流制老城区广泛采用源头分散式雨洪控制措施(LID),有效地减少了CSO污染。源头LID设施建设配合截流管网改造、合流制调蓄池建设和末端污水处理厂提标改造形成一套CSO污染控制系统。综合绿色基础设施和灰色设施建设,也逐渐成为控制CSO污染的主要方式。
但在CSO控制系统的规划与设计过程中,仍然存在最大化效益的同时如何最小化成本的问题。本研究利用Matlab、Python和SWMM模型建立了CSO控制系统建设成本与CSO削减率的多目标优化模型,研究北京市某合流制片区CSO控制系统的优化方法,为合流制区域治理方案的优化提供参考。
1 研究区域与方法
CSO控制系统的优化设计主要有2方面:经济性优化和功能性优化。经济性优化是以最优化理论为基础,以整体系统造价和运行维护费用最小为目标函数,寻求满足各类约束条件下的设计方案,通常采用的方法包括线性规划法、非线性规划法、动态规划法和智能优化算法等[5,6]。功能性优化设计主要通过构建模型的方法来进行CSO雨污水量削减的优化设计。
本研究通过Matlab软件实现非支配排序遗传算法(NSGA-Ⅱ)优化算法的编程,以及与其他软件间的衔接调用,借助Python软件实现数据的抓取和更新,并调用SWMM模型软件源程序对搭建好的模型实现自动运算。
1.1 研究区概况
1.1.1 研究区现状
研究区位于北京市某合流制区域,该区域总面积约为3 km2,区域内雨污水全部汇集至合流制管道内。2个合流制溢流口上游设有截污闸门,闸门附近设有高80 cm的溢流堰,管涵中闸门在旱季关闭,在雨季人工开启。当产生的雨污水量较少时,将直接被截入污水干管,收集至下游污水处理厂;当雨污水量较大漫过溢流堰时,则发生CSO现象。
1.1.2 研究区CSO控制系统组成
本研究区位于老城区,合改分面临耗费时间长、投入资金和实施难度大、难以达到预期目标等问题,因此采用“源头LID设施建设+中途截流管网改造+末端合流制调蓄池+末端污水处理厂前池建设”的CSO控制系统,系统设计如图1所示。
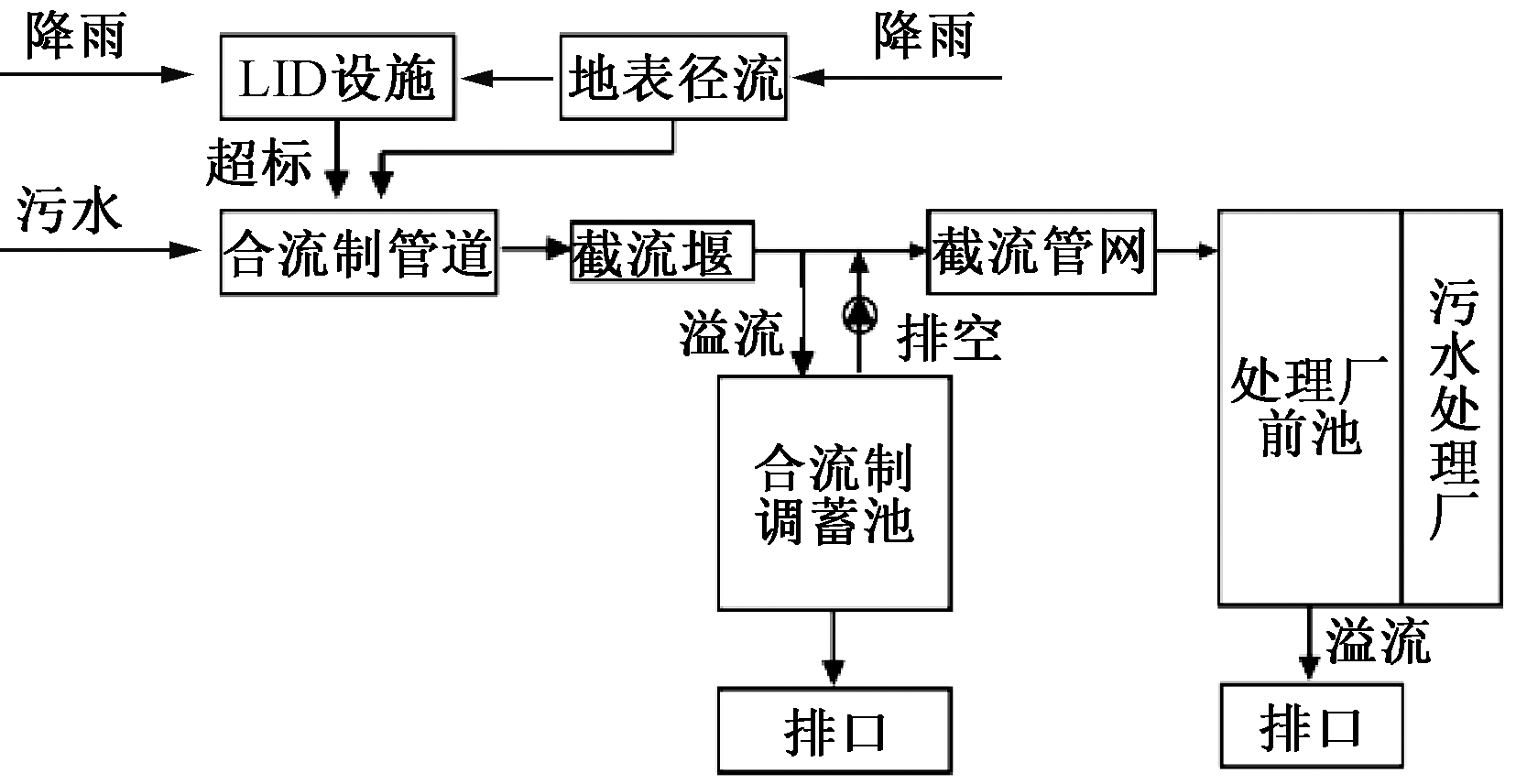
图1 CSO污染控制系统示意
Figure 1 Schematic diagram of CSO pollution control system
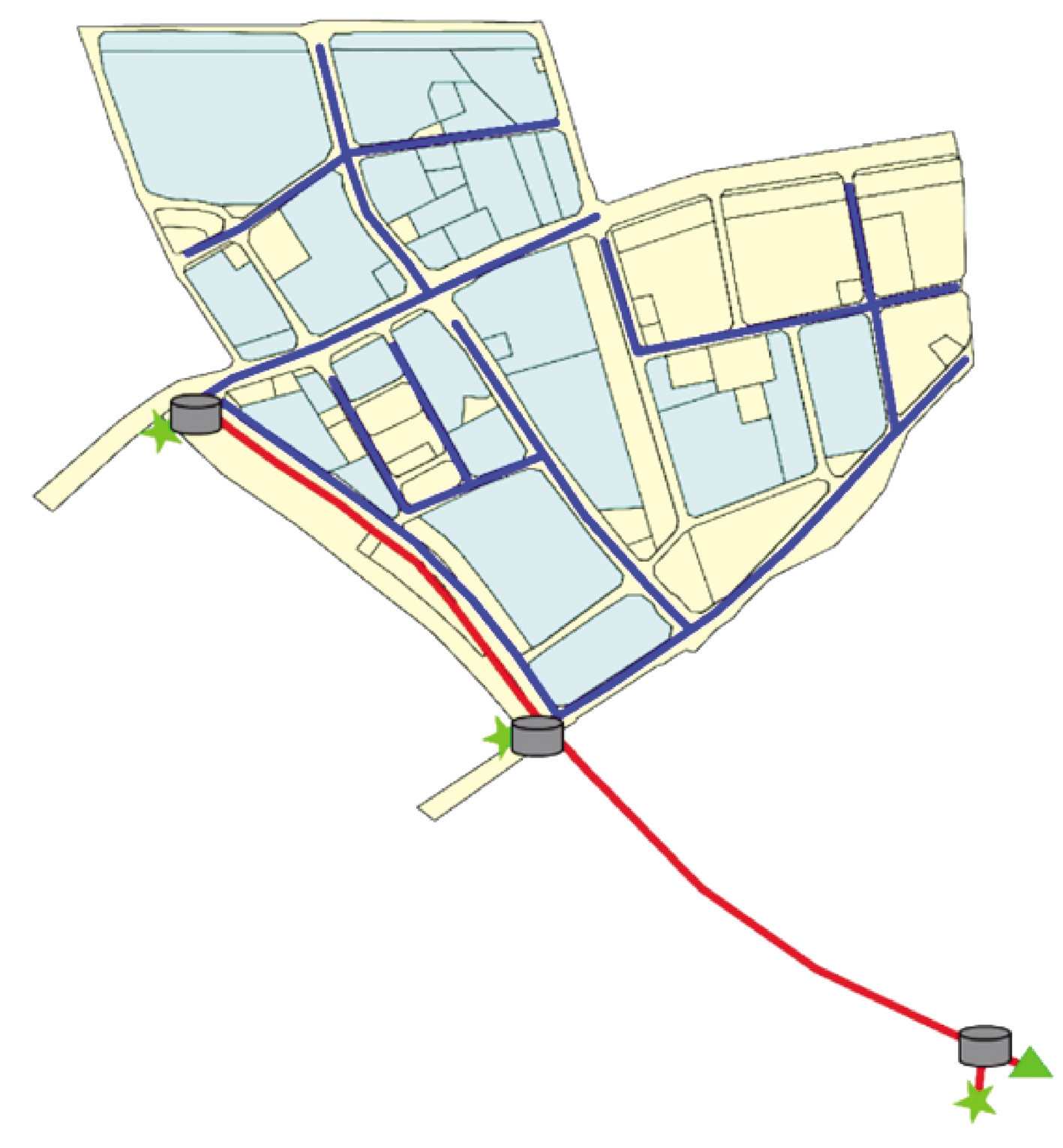
本研究将流入下游污水处理厂不能处理的雨污水认定为厂前溢流,将厂前溢流概化为排口溢流,通过在污水处理厂前建设前池来削减溢流雨污水量。2个合流制溢流口前同样需要建设调蓄池,故此CSO控制系统中共计3个调蓄池和3个溢流口。本研究系统中设定调蓄池在降雨时调蓄合流雨污水,降雨结束时将池内的雨污水排入污水处理厂,故将3个调蓄池设施都定义为末端设施。根据现场调查,结合当地实际建设情况,对能够进行源头LID设施建设的项目及其他CSO控制设施进行了统计,建设与改造项目分布情况如图2所示。
![]() LID改造区域;
LID改造区域; ![]() LID未改造区域;
LID未改造区域; ![]() 雨水主干管;
雨水主干管; ![]() 截流干管;
截流干管; ![]() 合流制溢流口;
合流制溢流口; ![]() 污水处理厂;
污水处理厂; ![]() 调蓄池。
调蓄池。
图2 改造项目分布示意
Figure 2 Schematic diagram of the distribution of the retrofitting projects
1.2 优化算法
由于本研究中的CSO污染控制系统的方案优化具有多目标、参数复杂、模型运行时间长等特点,故采用搜索范围较广、结果精确、优化过程自动化的NSGA-Ⅱ作为优化算法。NSGA-Ⅱ是一种模拟自然界生物群体进化过程的全局优化搜索算法,同时具备精英保留策略和非控制排序的特征,由多个决策变量、多个目标函数和多个约束组成。该算法以群体中的所有个体为对象,通过选择、交叉和变异等非支配排序遗传算法的主要步骤,对种群进行多目标下的优化。相比传统的数学算法可以节省大量的时间和人力,结果也更加精确可信。
本研究在NSGA-Ⅱ的优化过程中采用二元锦标赛选择法和群体精英保留策略,将父代种群和子代种群合并后,选择其中最优的个体构成下一代个体,提高优化过程中的收敛速度和优化效率[7]。
1.3 目标函数选取
本研究以降低系统建设成本和提高CSO削减率作为目标函数,在此基础上建立CSO控制系统的多目标优化模型。
1)建设成本。
建设成本由源头LID设施建设、截流管网改造及合流制调蓄池建设的工程造价组成,目标是在保证系统组成合理、提高CSO削减率的同时,尽量减少建设投资。
本研究中的各类源头LID设施以及合流制调蓄池的造价参考《海绵城市建设典型案例》[8]和北京市海绵城市建设实际工程确定,源头LID设施透水铺装为300元/m2,生物滞留池为500元/m2,雨水调蓄池为2500元/m3,末端调蓄设施合流制调蓄池和污水处理厂前池1500元/m3。源头LID设施和调蓄池建设成本采用式(1)、(2)计算:
![]()
(1)
式中:Z1为源头LID设施建设成本,元;Mij为第j项设施在第i个地块所占面积,m2;Bj为第j个设施的建设成本单价,元;m为源头LID设施的种类数目;n为地块数目。
![]()
(2)
式中:Z2为合流制调蓄池及污水处理厂前池建设成本,元;Vi为第i个调蓄池的建设体积,m3;B为调蓄池的建设成本单价,元。
由于管道工程中管道的埋深基本不变,成本实际上大多数来源于管网的翻修和替换[9],故本研究CSO控制系统中的管网改造成本参考国内相关研究成果[10]:
![]()
(3)
式中:Z3为截流管网改造成本,元;H为管道平均埋深,m;D为管道直径,m;l为管道长度;m。
建设成本目标公式如下:
G1=min(Z1+Z2+Z3)
(4)
式中:G1为区域的建设投资目标,元。
2)CSO削减率。
本研究中共涉及3个溢流口,将其总溢流削减率作为区域整体CSO削减率,该目标在模型中体现为式(5):
G2=max[1-(V1+V2+V3)/V0]
(5)
式中:G2为区域整体的合流制溢流雨污水控制目标,%;V0为改造前研究区域的合流制雨污水溢流量,m3;V1、V2、V3分别为溢流口1、2、3的合流制雨污水溢流量,m3。
1.4 约束条件
为更加准确快速地获取优化结果,结合实际建设条件,在多目标优化模型中设定5个约束条件,包括LID设施建设面积约束、合流制调蓄池和前池建设条件约束、管道建设条件约束、调蓄池排空时间约束和污水处理厂进水约束。
1)LID设施建设面积约束。
源头LID设施的建设面积是一项重要的约束条件[11],如停车场、人行道、屋顶、绿地等区域的总面积决定了海绵设施的最大面积,将其作为优化设计的约束条件,构成函数如下:
Aki≤MAki,∀k,I
(6)
式中:Aki为第i个LID设施占k分区的面积,m2;MAki为第i个LID设施占k分区的最大面积,m2。
2)合流制调蓄池和前池建设条件约束。
合流制调蓄池和前池在实际建设中往往受到选址地点最大建设面积和最大建设深度的影响,本研究中合流制调蓄池和前池的条件约束在模型中体现为最大建设体积,构成函数如下:
Vi≤MVi,∀I
(7)
式中:Vi为第i个调蓄池或前池的建设体积,m3;MVi为第i个调蓄池或前池的最大建设体积,m3。
3)管道建设条件约束。
将下游管道≥上游管道管径作为CSO控制系统截流管道建设的约束条件,且改造管径不小于改造范围外的上游管段管径,不大于改造范围外的下游管径。
D≥Dn+1≥Dn≥D0
(8)
式中:D为污水处理厂前污水干管管径,m;Dn为管段第n个截流管段管径,m;D0为管段第1个截流管段管径,m。
4)调蓄池排空时间约束。
为保证合流制调蓄池在时间接近的2场降雨中发挥作用,设定调蓄池排水泵站在雨停时开启,排空时间由下游污水厂处理能力决定,下游污水处理厂运转负荷为3.5万m3/d,最大负荷为4万m3/d,有5000 m3/d的剩余负荷量可供合流制区域利用,故合流制调蓄池泵站运转功率须满足式(9):

(9)
式中:Pn为第n个调蓄池泵站的运行功率,m3/s;P0为下游污水厂所能容纳的剩余负荷量,本次研究中固定值为0.058 m3/s;Vn为第n个调蓄池的实际调蓄空间,m3。
5)污水处理厂进水约束。
合流制污水由前池进入污水厂的过程中,由于污水厂存在处理能力上的限制,故需要满足最大进水量约束,如式(10)所示:
Q0≤Q0max
(10)
式中:Q0为污水处理厂入厂流量,m3/s;Q0max为污水处理厂最大入厂流量,m3/s。
1.5 SWMM模型及参数
本研究团队曾搭建研究区SWMM模型,深入研究海绵城市建设条件下CSO控制方案的建设效果,本研究的SWMM模型搭建和LID参数采用既有研究成果[12]。模型采用研究区域3年一遇24 h设计降雨。
2 结果分析与讨论
2.1 区域CSO削减率优化结果
2.1.1 不同类型方案与区域CSO削减率的关系
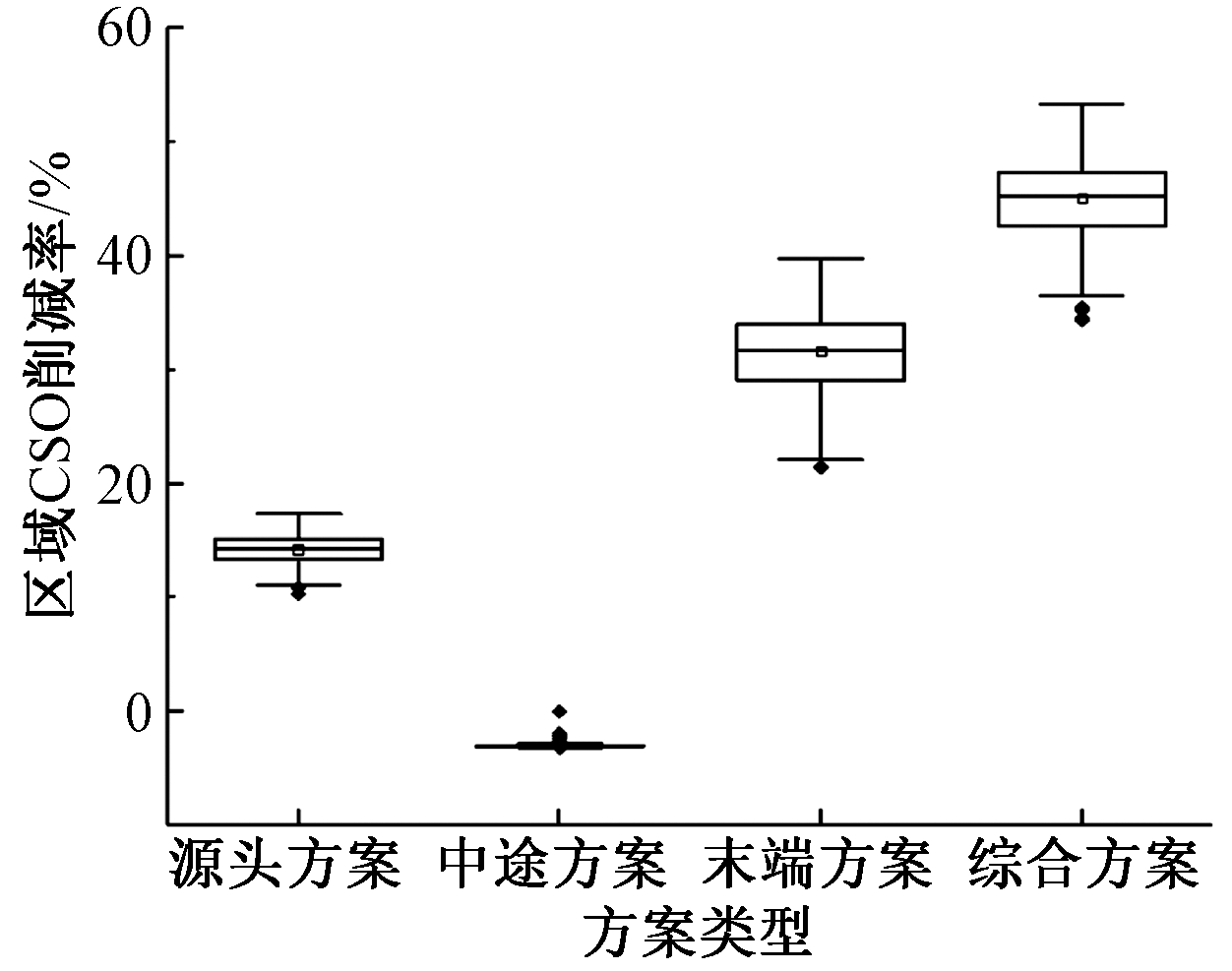
4类方案CSO削减率如图3所示。可知:综合方案为本研究的优化结果,并进一步将优化结果拆分为3类方案,并定义为源头方案、中途方案与末端方案,其中源头方案即仅实施源头LID设施建设部分,中途方案即仅采用截流管网改造部分,末端方案即为仅采用末端调蓄池建设部分。
![]() 25%~75%; ——中位线;
25%~75%; ——中位线;![]() 均值;
均值;![]() 异常值。
异常值。
图3 4类方案CSO削减贡献率
Figure 3 Schematic diagram of CSO reduction contribution rates of four schemes
源头、中途、末端和综合方案的CSO削减率如表1所示,对比得出以下结论:1)以CSO雨污水量控制为指标时,在3年一遇设计降雨条件下末端合流制调蓄池的建设发挥较好作用,另两类设施的建设效果相对较低,仅建设末端合流制调蓄池区域整体溢流削减率为21.46%~31.67%;2)从整体上看,在不涉及其他项目改造的前提下,截流管网改造对区域整体的贡献为负值,在3年一遇设计降雨条件下单独的截流管网改造会使区域溢流量增多,所以截流管网改造还需要配合其他设施改造和建设才能发挥积极作用;3)综合源头LID设施建设、截流管网改造和末端调蓄设施的CSO控制系统综合方案,相对于仅建设末端合流制调蓄池的末端方案建设效益有相应提高,综合方案能使区域整体溢流削减率达到34.33%~53.42%。
表1 4类方案CSO削减率统计表
Table 1 Statistical table of CSO reduction rate of four schemes %

CSO削减率源头方案中途方案末端方案综合方案最大值17.34-1.8939.8353.42最小值10.27-3.2321.4634.33平均值14.24-2.9531.6745.09
2.1.2 溢流口位置与CSO削减率的关系
将综合方案与源头、中途、末端3类方案结果作进一步对比分析,取区域中3个溢流口的溢流削减率进行对比研究,如图4所示。

![]() 溢流口1溢流削减率;
溢流口1溢流削减率; ![]() 溢流口2溢流削减率;
溢流口2溢流削减率; ![]() 溢流口3溢流削减率;
溢流口3溢流削减率; ![]() 整体区域溢流削减率;
整体区域溢流削减率; ![]() 25%~75%; ——中位线;
25%~75%; ——中位线;![]() 均值;
均值;![]() 异常值。
异常值。
图4 各类型方案不同溢流口削减率均值示意
Figure 4 Schematic diagram of mean value of different discharge reduction rates in different schemes
通过对比不同类型方案和不同溢流口的CSO削减率,发现源头方案、中途方案、综合方案的3个溢流口CSO削减率从上游到下游依次降低。对于综合方案,降雨时上游溢流口CSO的削减一部分依靠源头LID设施的雨量滞蓄分担减少雨水汇入;另一部分由于截流管网的改扩建增大了排水能力而排入下游,下游管道承接的上游管道来水流量增大,且越靠近下游管道,管道中的上游来水流量越大,进而导致越靠近下游CSO的削减越困难。截流管网改造导致区域CSO削减率为负值的原因在于截流能力的增加使得改造后满管情况大幅削减,上游雨水管网收水能力增强,上游区域产生的一部分积水被收集到管道,从而导致下游管道流量加大。末端方案与其他3类方案结果存在不同规律,受末端调蓄设施建设条件限制,溢流口1溢流削减率相对较低,而溢流口2溢流削减率相对较高,说明合理建设末端设施可以大幅度削减中下游溢流口的CSO。
2.2 建设成本优化结果
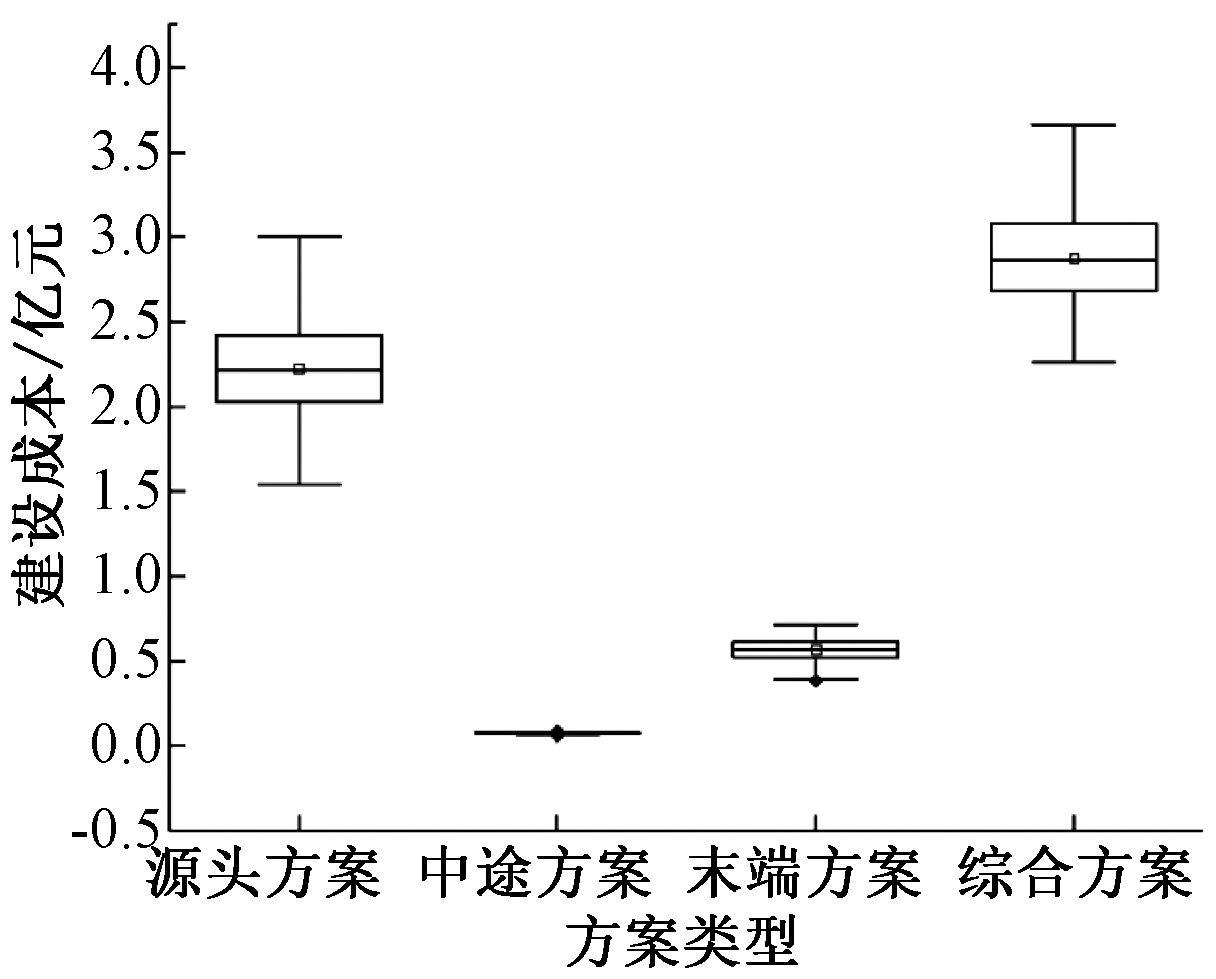
为分析区域CSO削减率与不同类型方案建设成本间的关系,将优化结果方案拆分为源头方案、中途方案与末端方案分别进行研究,单独研究某一方案时不涉及其他2类改造方案。建设成本优化结果如图5所示。区域整体建设总成本为2.26亿~3.67亿元,源头LID设施建设成本最高,中途截流管网建设成本最低,末端调蓄池建设成本相对源头LID设施建设部分较低。
![]() 25%~75%; ——中位线;
25%~75%; ——中位线;![]() 均值;
均值;![]() 异常值。
异常值。
图5 4类方案建设成本优化结果
Figure 5 Optimization result of construction cost of four schemes
源头方案建设成本与区域CSO削减率关系如图6a所示,两者呈正相关。源头LID设施建设对于CSO削减率的贡献较低,成本较高。但源头LID设施基于可持续发展的理念,与截流管网改造、合流制调蓄池建设相比,更多的回报在于雨水回用、地下水涵养、景观提升等诸多方面,关于源头LID建设与截流管网改造、合流制调蓄池建设的优化还需要综合考虑[13-15]。
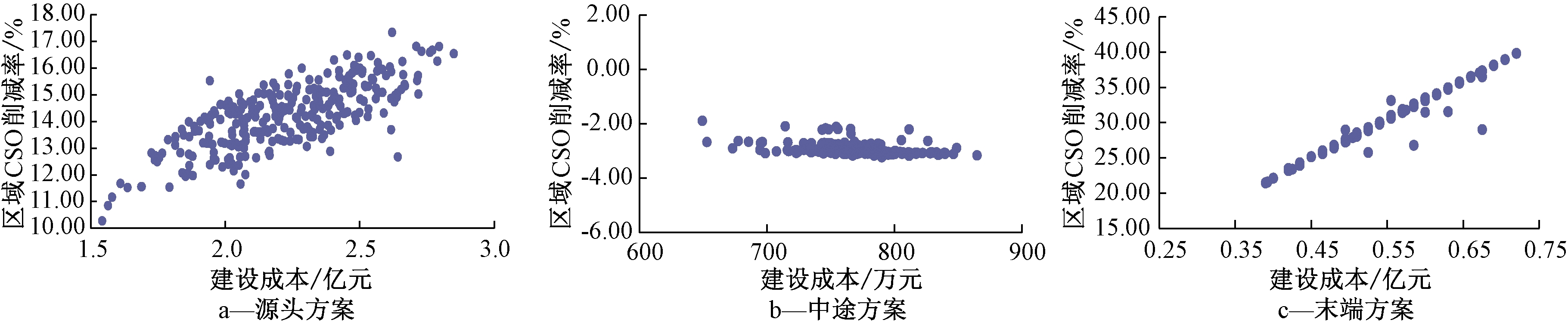
图6 建设成本与CSO削减率关系
Figure 6 Relationship between construction costs and CSO reduction rates
中途方案效果如图6b所示,中途方案的建设成本对区域整体溢流削减率影响较小。中途方案在系统建设成本中的平均占比最少,结合前文结论,单独的截流管网改造会使区域整体溢流量增加,只有配合其他类型设施建设才能发挥正面作用。
末端方案效果如图6c所示,末端方案的建设成本与区域整体溢流削减率大体上呈线性正相关,随着建设成本的增加,CSO削减率提高。区域CSO削减率的贡献平均值为31.67%,成本居中。但由于调蓄池的运维和新增污水的处理需要一定的费用,因此比选时不应仅考虑建设成本。
2.3 优化方案的选择策略研究
借助NSGA-Ⅱ对CSO控制系统建设方案进行优化并得到一系列优化结果(Pareto解集),如图7所示。从成本与效益间关系可知:随着CSO控制系统建设成本增加,区域整体溢流削减率有增高趋势,但建设成本的增加并不是决定性因素。
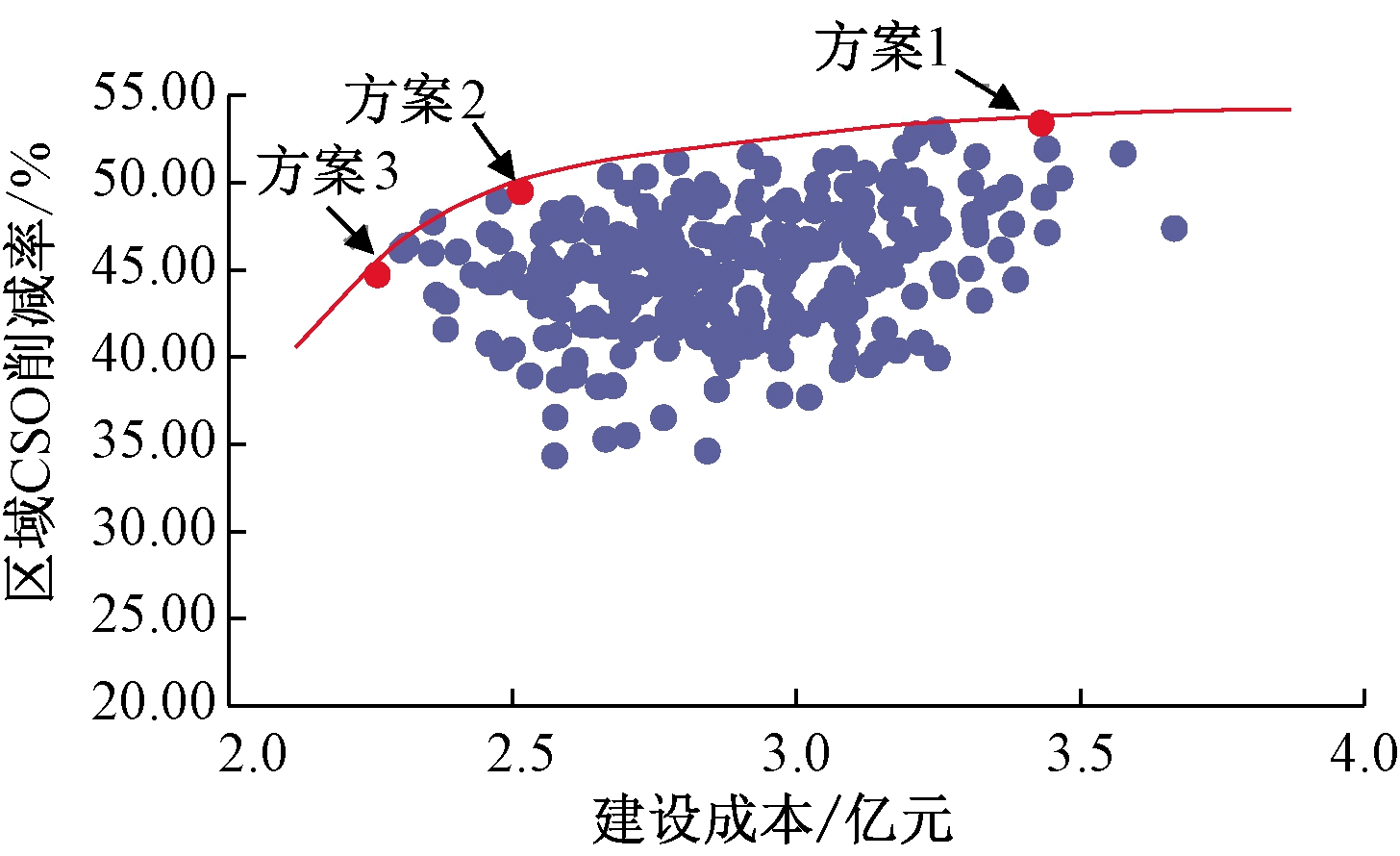
图7 优化结果中的相对较优方案
Figure 7 The optimal schemes in the optimization results
在工程的实际建设过程中规划决策者需要均衡建设成本与建设效益,二者难以同时兼顾。遵循减少建设成本与提高建设效益的原则,从优化结果中筛选位于图7上边界的相对较优方案,得到具有代表性的3套方案,方案结果如表2所示。方案1是相对较优方案中建设成本最高的,区域整体CSO削减率也相对最高;方案3建设成本为3套方案里最低,而且区域整体CSO削减率是相对较优方案中最低的,为44.72%,在所有优化结果中相对居中;方案2位于边界线上转折处,转折点之后随着建设成本增加,区域整体CSO削减率的增加不再明显。因此,当规划建设决策者侧重CSO控制系统的建设成本时,可选择方案3;侧重区域整体CSO削减率时,可选择方案1;如果寻求两者较均衡的方案时,可选择方案2。
表2 3套相对较优方案的建设成本与CSO削减率
Table 2 Construction cost and CSO raduction rates of three optimal schemes

项目系统建设成本/亿元区域整体CSO削减率/%方案13.4353.42方案22.5149.49方案32.2644.72
3 结论与展望
本研究利用Matlab、Python和SWMM模型建立了CSO控制系统建设成本与CSO削减率的多目标优化模型,在3年一遇设计降雨条件下,以区域整体溢流量削减率和工程建设成本作为控制目标进行优化,得到以下结论:
1)区域整体的CSO削减率随着控制系统建设成本增加存在增高趋势,但CSO削减率不仅受建设成本影响,还受CSO控制系统配置合理性的影响,相同建设成本下,合理的规划设计可得到更好的效益。
2)CSO削减率受末端调蓄池建设的影响最大,受源头LID设施建设和中途管网改造的影响较小;越靠近上游的溢流口溢流削减率越高,越靠近下游的溢流口溢流削减率越低;综合源头、中途、末端3类方案的CSO控制系统可达到较好的效果,在CSO污染控制系统建设方面三者都是有必要的。
3)仅在以降低系统建设成本和提高CSO削减率为双目标的前提下,末端设施相比于源头LID设施更合理。但是源头LID设施更符合可持续发展理念,CSO控制方案的优化需要综合考虑其他建设效益作进一步研究。
本研究受资料和其他研究条件限制,CSO控制系统优化过程中的经济性仅考虑了固定的建设成本,因此结论有一定的局限性。未来的研究和实践中,还需将源头LID设施、调蓄池、雨污水处理等的运维费用以及LID设施的其他效益纳入优化目标,实现更多目标的方案优化。
[1] 唐磊, 车伍, 赵杨, 等. 合流制溢流污染控制系统决策[J]. 给水排水, 2012, 38(7):28-34.
[2] 杨雪, 车伍, 李俊奇, 等. 国内外对合流制管道溢流污染的控制与管理[J]. 中国给水排水, 2008, 24(16):7-11.
[3] 车伍, 刘燕, 李俊奇. 国内外城市雨水水质及污染控制[J]. 给水排水, 2003,29(10):38-42.
[4] 徐一茗. 合流制管道溢流的影响因素及其污染治理措施[J]. 山西建筑, 2010, 36(34):170-172.
[5] 韩东刚, 王赫婧, 尤学一, 等. 基于图论与枚举算法的城市污水管网优化设计[J].中国给水排水,2013,29(15):141-145.
[6] 曹相生, 刘杰, 刘婷, 等. 基于枚举算法的雨水管网优化设计[J]. 中国给水排水, 2010, 26(7):37-39.
[7] IngeTeng. [多目标优化算法应用]新高考模式下遗传算法在排课问题中的应用[EB/OL]. (2019-03-13)[2019-10-21].https://blog.csdn.net/loveC_/article/details/88542429.html.
[8] 章林伟. 海绵城市建设典型案例[M]. 北京:中国建筑工业出版社, 2017.
[9] 李芊, 张明媛, 袁永博. 基于MOPSO的雨水管网多目标改建优化[J]. 给水排水,2016,52(5):127-131.
[10] 王赫婧. 城市雨水管网多目标优化设计研究[D]. 天津:天津大学, 2012.
[11] SEBTI A, FUAMBA M, BENNIS S. Optimization model for BMP selection and placement in a combined sewer[J]. Journal of Water Resources Planning and Management, 2015, 142(3): 04015068.
[12] GONG Y W, CHEN Y, YU L, et al. Effectiveness analysis of systematic combined sewer overflow control schemes in the sponge city pilot area of Beijing[J]. International Journal of Environmental Research and Public Health, 2019, 16(9): 1503.
[13] HUANG Y L, HUANG C, LIU H J, et al. Optimization of low impact development layout designs for megacity flood mitigation[J]. Journal of Hydrology, 2018, 564: 542-558.
[14] 沈冰洁, 潘迪. 基于海绵城市理念的海绵校园景观优化研究[J]. 现代农村科技,2018(9):77-78.
[15] ECKART K, MCPHEE Z, BOLISETTI T. Multiobjective optimization of low impact development stormwater controls[J]. Journal of Hydrology, 2018,562:546-576.
[16] 李倩, 宫俊, 唐加福. 基于改进NSGA-Ⅱ的交叉培训规划多目标优化[J]. 东北大学学报(自然科学版), 2011,32(12):1696-1699.