0 引 言
由于全球气候变化及人类高强度活动等因素共同作用,极端天气频发,人类社会屡遭洪涝灾害影响[1]。EM-DAT国际灾害数据库统计显示,洪灾导致经济损失占全球经济损失的1/3以上,受各种自然灾害影响的人口中有2/3受洪灾影响[2],可见洪灾对人类生活影响巨大,已成为国际性问题。最近研究发现,气候变化可能会导致更多的极端降雨事件,使洪涝灾害风险进一步增大[3]。故及时对洪灾进行损失分析及风险评估,制定合理的战略应对至关重要。当前此类工作广泛采用水动力模型进行数值模拟计算实现。王志力等[4]建立了适应于结构网格的有限体积数学模型,对广西蓬莱滩河段进行模拟且结果与实测相符,为后续洪涝工作提供了指导;苑希民等[5]构建了一种漫溃堤洪水联算全二维水动力模型,对黄河宁蒙段河道与左右岸灌区进行模拟,为该地区防灾决策提供了依据。但在高分辨率大尺度模拟中计算单元多、时间步长短的情况下,此类模型在运行计算效率方面仍存在不足[6,7]。
GPU(graphics processing unit)加速技术为大规模城市雨洪模拟提供了可能,并已有许多学者开始使用该技术来加速水动力模型。Lacasta[8]提出一种基于GPU计算平台利用FV方法求解二维浅水方程的途径,加速性能显著;赵旭东等[9]开发了基于GPU的非结构网格有限体积法海洋模型,完成对长山群岛潮流过程的高性能数值模拟。但以上模型均未运用到城市雨洪过程模拟中。Liang等[10]采用GPU加速技术,构建了一种能捕捉地表水流快速运动过程的水动力模型,实现了大尺度城市雨洪模拟;侯精明等[11]提出一套基于GPU加速技术的地表水动力数值模型,可大范围高效高精度模拟城市雨洪过程。这些模型已被成功应用于不同地区的城市雨洪模拟,能够以极高分辨率完成对中等以上规模区域的实时城市洪涝模拟预报。
但以上研究GPU平台单一,并未系统量化城市雨洪过程,更未研究比较不同GPU平台下的加速计算效率。本文将GPU技术应用至二维水文水动力城市雨洪数值模型中,选取典型城市作为研究区域,系统量化分析了CPU及不同GPU计算平台下的计算效率,可为GPU在城市雨洪模拟加速的应用给出重要参考,也为更大规模的计算提供了可能。模拟结果对城市雨洪快速预报具有指导意义。
1 模型介绍
城市雨洪过程模拟采用二维水动力学模型—GAST模型(GPU Accelerated Surface Water Flow and Transport Model)[11-14],该模型适用于任何复杂的网络,精度高、效率快,已较好地模拟了城市内涝[11]、泥沙输移[12]、流域洪水演进[13]等过程,能对大尺度雨洪过程进行精确模拟,优势显著[14]。同时该模型引入了GPU加速并行计算技术,使模型计算速度显著提升。
1.1 控制方程
数值模型的控制方程为二维浅水方程(SWEs),守恒格式的矢量形式[15]表示如下:
(1)
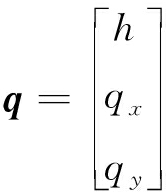
(2)
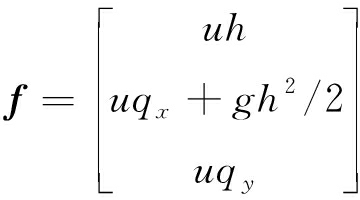
(3)
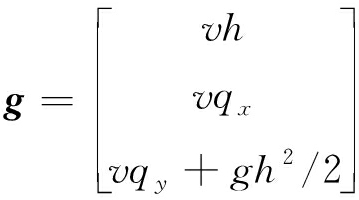
(4)
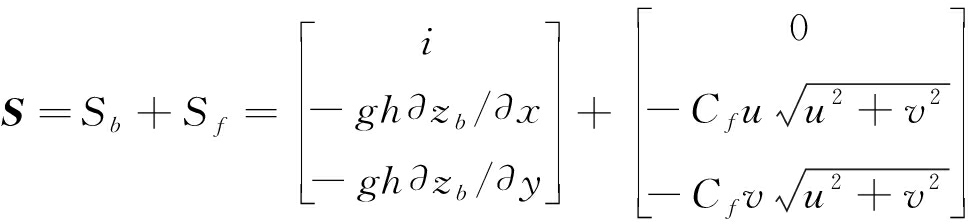
(5)
式中:x、y、t分别为笛卡尔空间坐标、时间坐标;q为变量矢量,包括水深h,m;qx和qy为x、y两个方向上的单宽流量,m2/s;u、v分别表示x、y方向上的流速,m/s;f和g分别为x、y方向上的通量矢量;S为源项矢量,包括降雨或下渗源项i、底坡源项Sf及摩阻力源项Sb ;Zb为河床底面高程,m;谢才系数Cf=gn2/h1/3,m1/2/s,其中n为曼宁系数。
1.2 数值方法
本模型采用Godunov有限体积法求解二维浅水方程,通过Riemann的近似HLLC(Harten-Lax-van Leer-Contact)求解器计算单元界面处的质量通量及动量通量;使用静水重构法处理干湿边界处负水深问题,干湿网格判定为0.000001 m[16,17];采用底坡通量法求解水深的变化[18];摩阻源项采用改进的分裂点隐式法提高计算稳定性[19];并利用二阶显式Runge Kutta法保证时间积分的二阶精度[20];采用MUSCL格式有效地解决由非物理现象所引起的计算的不稳定性和物质动量的不守恒性。
2 基于GPU加速的并行计算技术
2.1 基于GPU加速的并行计算平台搭建
计算平台考虑6种类型的GPU,在不同GPU平台下,开展城市雨洪过程模拟。GPU类型及计算的关键参数见表1。可知:NVIDIA Tesla P100的计算性能是最佳的,流处理器数目远超于其他类型的GPU。计算平台选用的CPU类型为Intel®CoreTMi7-7700,所有应用计算只基于该CPU进行计算,CPU类型及关键参数如表2所示。
表1 GPU关键参数
Table 1 Key parameters of GPU computation
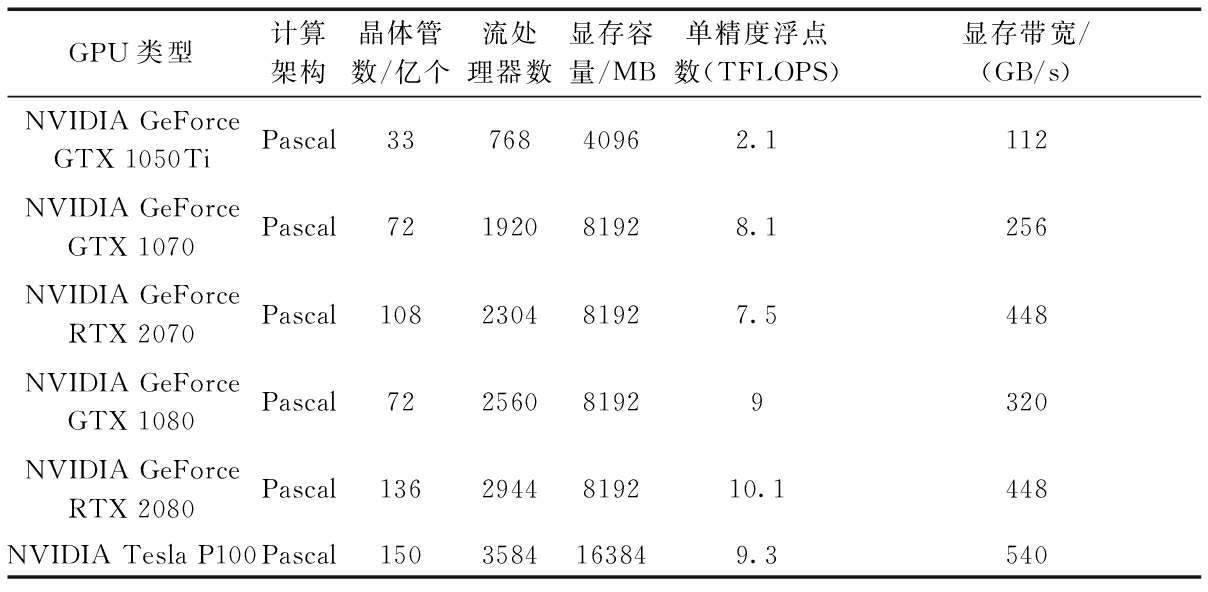
GPU类型计算架构晶体管数/亿个流处理器数显存容量/MB单精度浮点数(TFLOPS)显存带宽/(GB/s)NVIDIA GeForceGTX 1050TiPascal3376840962.1112NVIDIA GeForceGTX 1070Pascal72192081928.1256NVIDIA GeForceRTX 2070Pascal108230481927.5448NVIDIA GeForceGTX 1080Pascal72256081929320NVIDIA GeForceRTX 2080Pascal1362944819210.1448NVIDIA Tesla P100Pascal1503584163849.3540
表2 CPU关键参数
Table 2 Key parameters of CPU computation

CPU 类型计算架构主频线程数三级缓存最大内存支持Intel CoreTMi7-7700Haswell3.6 GHz8线程6 MB8 GB
2.2 基于GPU加速的并行计算过程实现
该模型采用C++及CUDA语言进行编程实现GPU加速的并行计算过程。在CUDA编程模型中,以CPU作为主机,GPU作为协处理器。CPU负责处理逻辑事务及串行运算,GPU则负责执行并行计算任务。在执行并行计算任务时,首先将数据读入CPU,并在每个网格中初始化网格信息、边界条件、计算参数等。分配至相应GPU设备空间后将数据复制到GPU显存,待计算完毕,将结果同步复制至CPU。具体计算过程如图1所示[11]。但当数据在CPU内存和GPU内存之间传输时,必须调用CUDA运行API。若CPU内存与GPU内存之间的数据交换过于频繁,其数据交换产生延迟会降低程序性能。故此,为避免结果输出过程中的频繁数据交换延长计算时间,在本文对比分析中,模拟时间为4 h,仅在模拟结束后再进行结果输出。
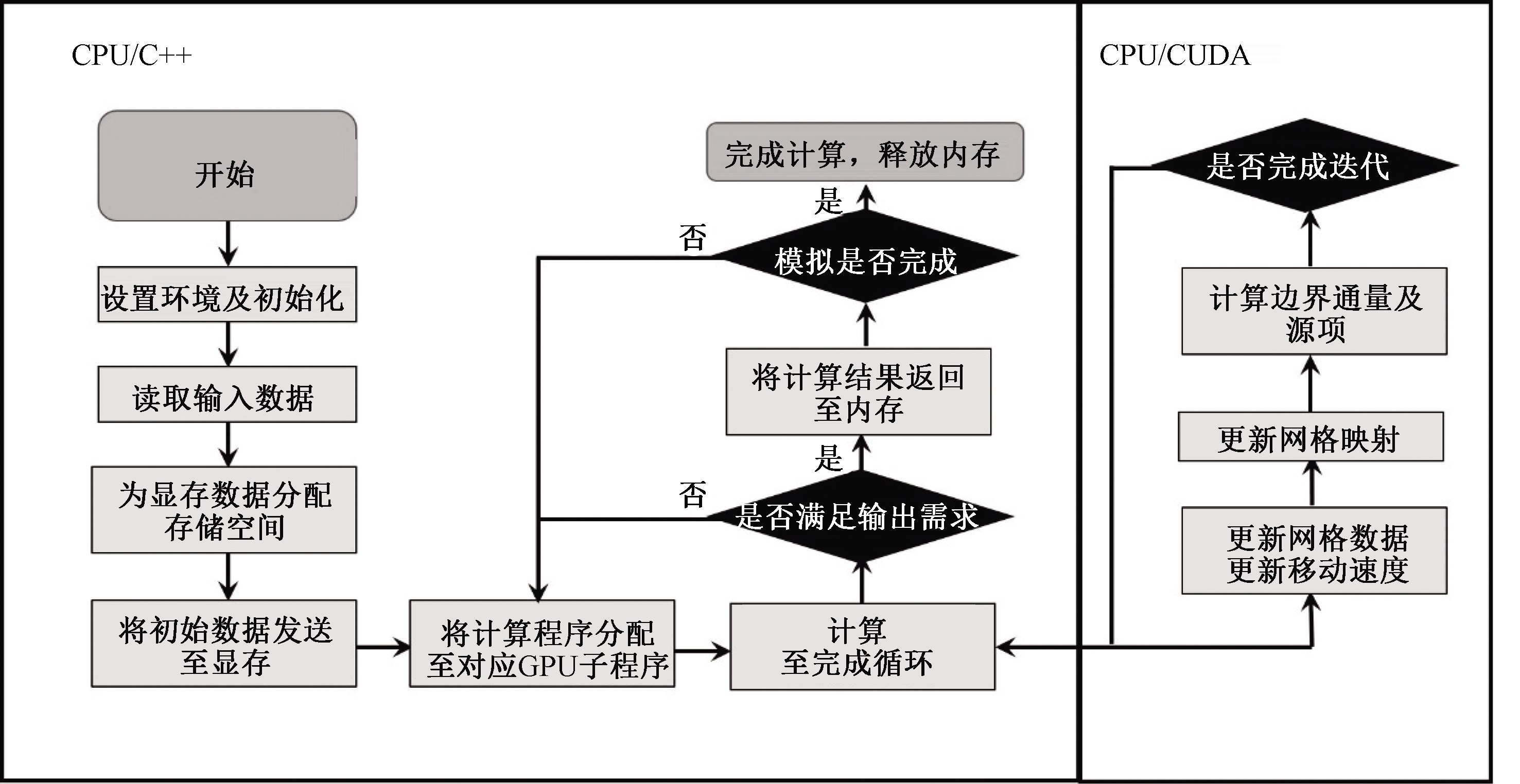
图1 GPU计算流程[11]
Figure 1 Computation flow of GPU
3 城市雨洪过程数值模拟
基于搭建好的GPU加速的并行计算平台,利用二维水动力学模型——GAST模型,以西咸新区沣西新城作为典型城市研究区域,对不同降雨重现期及网格分辨率情形下的城市雨洪过程进行了模拟,并进一步量化分析GPU加速技术应用在城市雨洪过程的计算效率。其中模型计算采用开放边界,四周无入流,采用双精度格式定义变量。计算过程库朗数采用0.5。
3.1 研究区域概况
西咸新区沣西新城是国家第一批海绵城市试点,位于陕西省咸阳市建成区以南,地理位置108.71°E、34.29°N,为大陆性季风气候,降雨集中于7—9月,多以暴雨形式出现,内涝灾害频发[21]。所选取研究区域沣西新城海绵城市建设核心区总面积约22.5 km2,其区位图如图2所示。
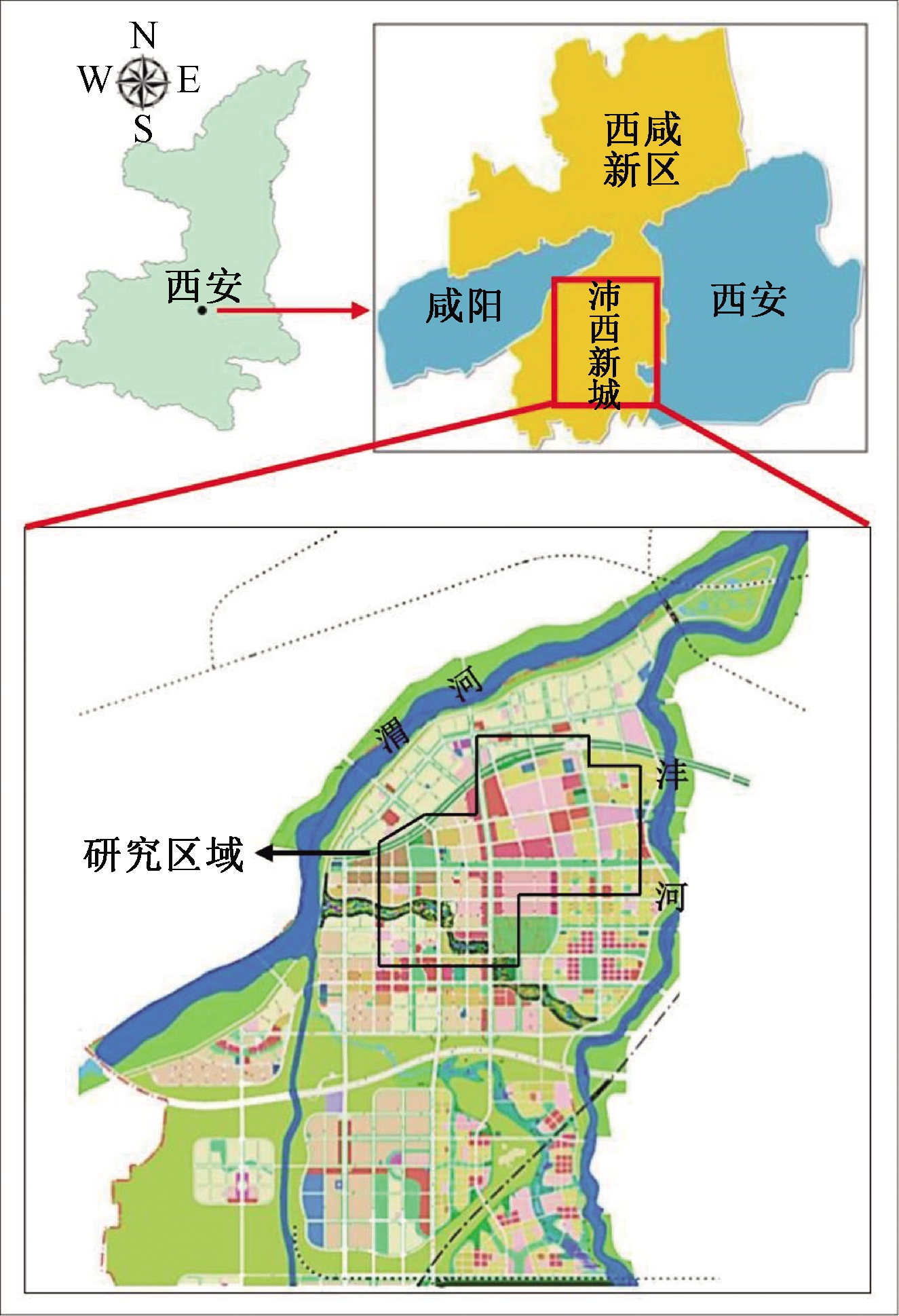
图2 沣西新城区位示意[21]
Figure 2 Location of Fengxi New Area
3.2 基础数据收集
基础数据包括降雨数据、地形数据、土地利用分类及相关下垫面条件数据。
1)降雨数据。研究区域降雨数据是根据暴雨强度公式得到的设计降雨,由沣西新城设计暴雨公式[21]计算得出。选用降雨重现期分别为5年和50年,降雨历时为120 min的设计暴雨,设计暴雨过程如图3所示。暴雨强度公式如式(6)所示:
(6)
式中:i为暴雨强度,mm/h;;P为重现期,a;t为降雨历时,min。
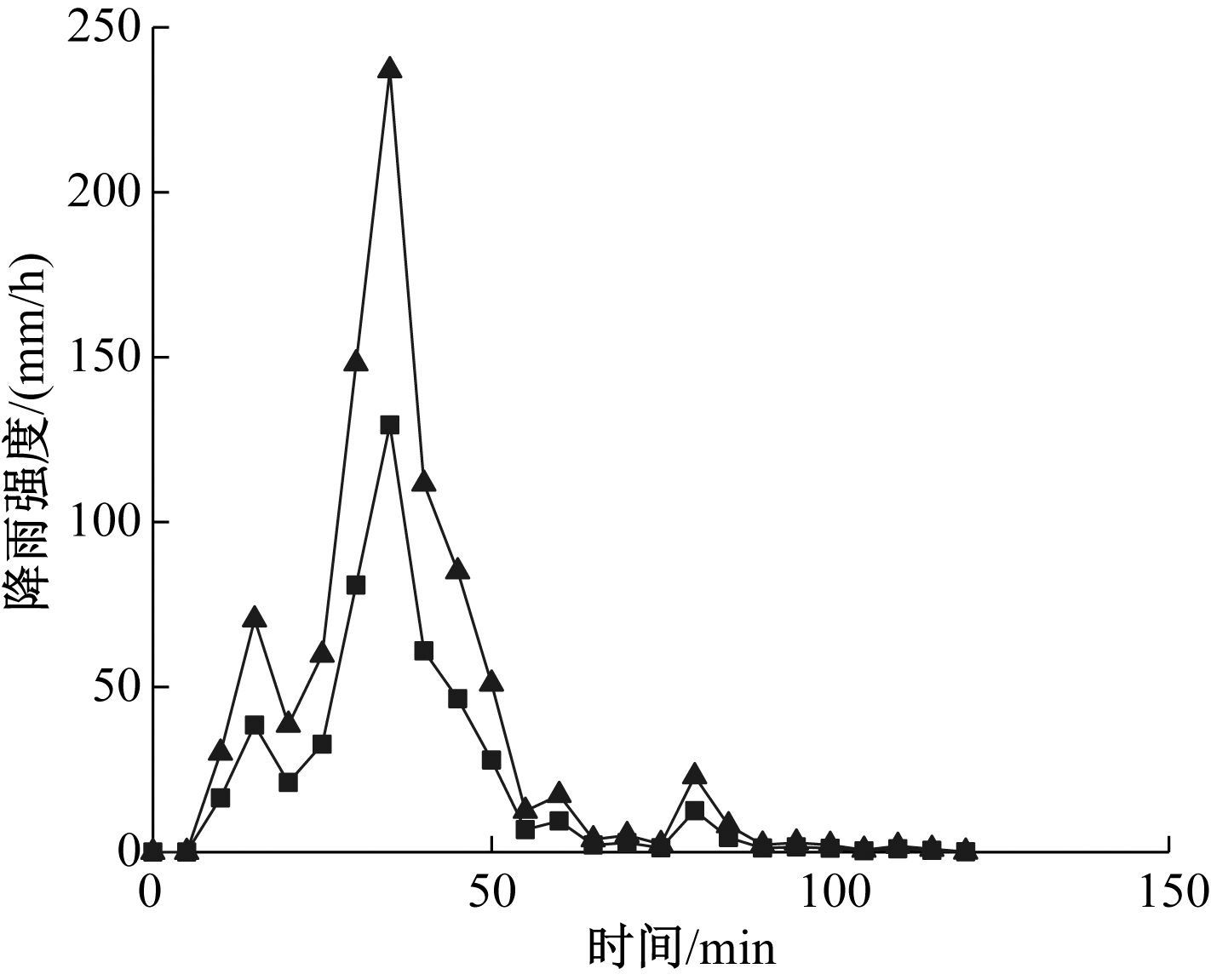
![]() … 5年一遇;
… 5年一遇; ![]() … 50年一遇。
… 50年一遇。
图3 不同重现期设计降雨过程
Figure 3 The raining courses with different design hyetograph
2)地形及下垫面条件。为获取高精度地形数据,采集地形数据过程中,采用无人机载激光雷达技术对研究区域进行航测,高精度地形数据及正射影像见图4。基于此将研究区域划分为居民用地、裸地、林地、草地、道路5类土地利用类型(图5),城市管网排水能力以等效下渗方法处理,参考文献[11]。各土地利用类型下渗率及对应的曼宁系数则根据相关文献确定[22]。

注:1 Mile=1.609 km,下同。
图4 区域数字高精度地形
Figure 4 High-resolution DEM data in the study area
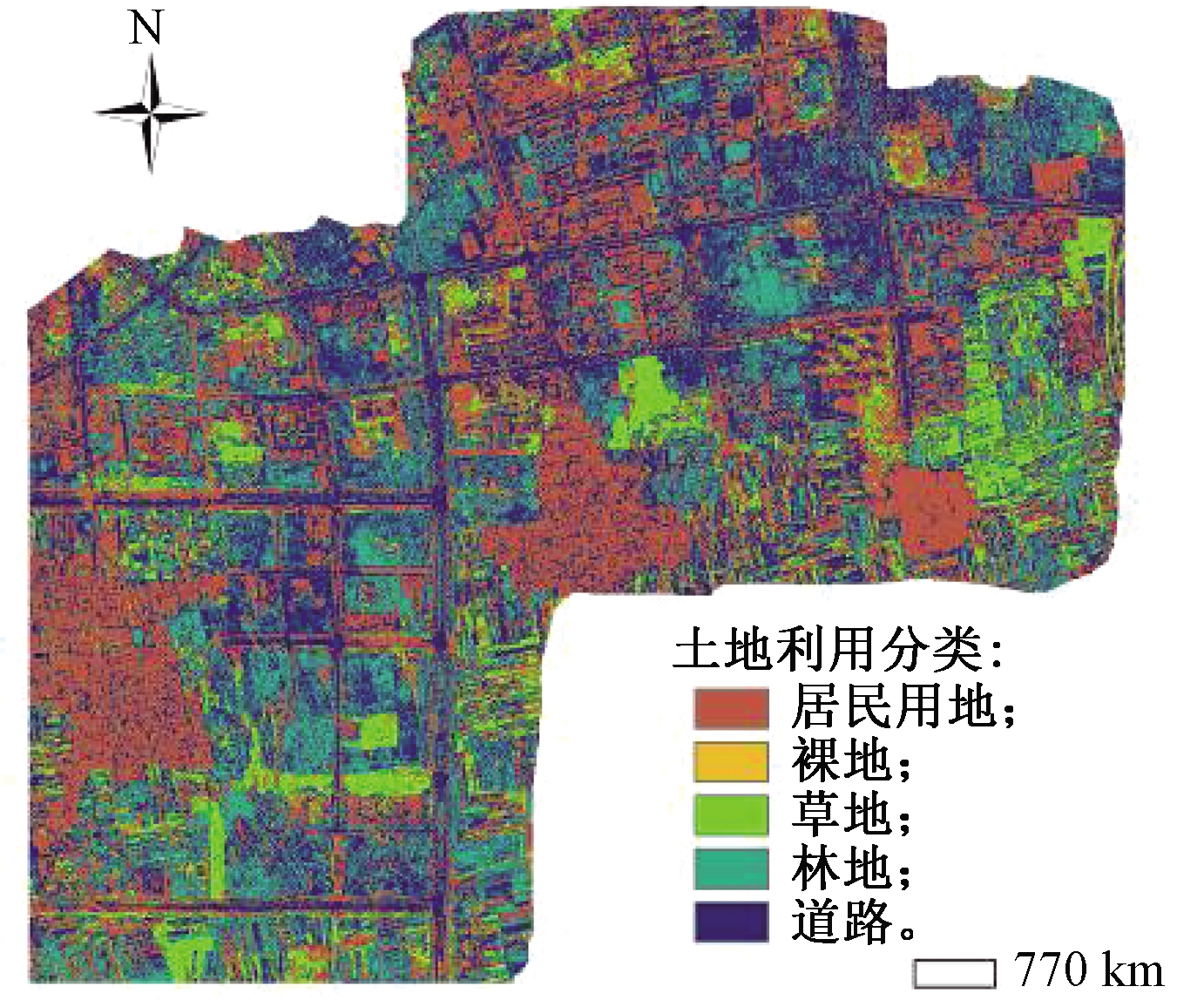
图5 土地利用类型
Figure 5 Land use map of the study area
3.3 模型验证
本文采用GAST模型对所选取研究区域2016年8月25日实测降雨进行模拟,得到内涝积水水深及面积,并与实测数据进行对比[11],结果见表3,各点积水程度模拟值与实测数据相近,表明模拟的城市雨洪过程及内涝积水情况与实际过程相符。可见模型各参数设计合理,模拟精度较高,适用于城市雨洪过程模拟研究。
表3 模拟积水程度与实测情况对比
Tabal 3 Comparison of the simulated and measured inundations
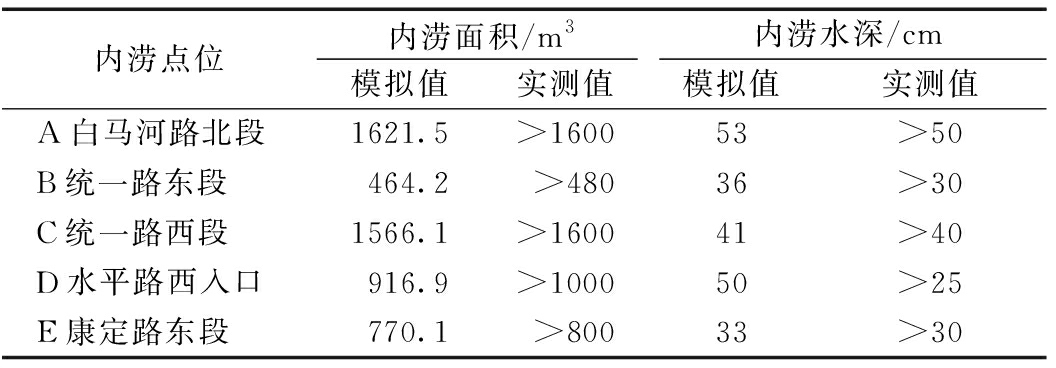
内涝点位内涝面积/m3内涝水深/cm模拟值实测值模拟值实测值A白马河路北段1621.5>160053>50B统一路东段464.2>48036>30C统一路西段1566.1>160041>40D水平路西入口916.9>100050>25E康定路东段770.1>80033>30
3.4 计算效率对比结果分析
基于已构建的沣西新城城市雨洪模型,通过对该地区城市雨洪过程进行模拟,探讨了2种降雨重现期(5年和50年一遇)在不同计算平台条件下的城市雨洪过程模拟计算效率。研究区域的网格分辨率为1,2,5,10 m,分别对应的网格数为21484522(情形1)、5369855(情形2)、859682(情形3)、215131(情形4)。通过对城市雨洪过程CPU和GPU模拟时间及对比结果分析(详见表4),将1核Intel®CoreTMi7-7700作为比较标准,设定其加速比为1,在考虑所有情形方案下,基于NVIDIA Tesla P100的城市雨洪模拟计算效率远高于其他类型GPU,相比较Intel®CoreTMi7-7700(1核)的提升效果(提速比)高达158.72倍,且可高效模拟千万级网格尺度城市雨洪过程(情形1)。GPU计算能力远超CPU。
表4 城市雨洪过程CPU和GPU模拟时间及对比
Table 4 Total execution time and speedup by CPU and GPU in urban rain-flood simulation
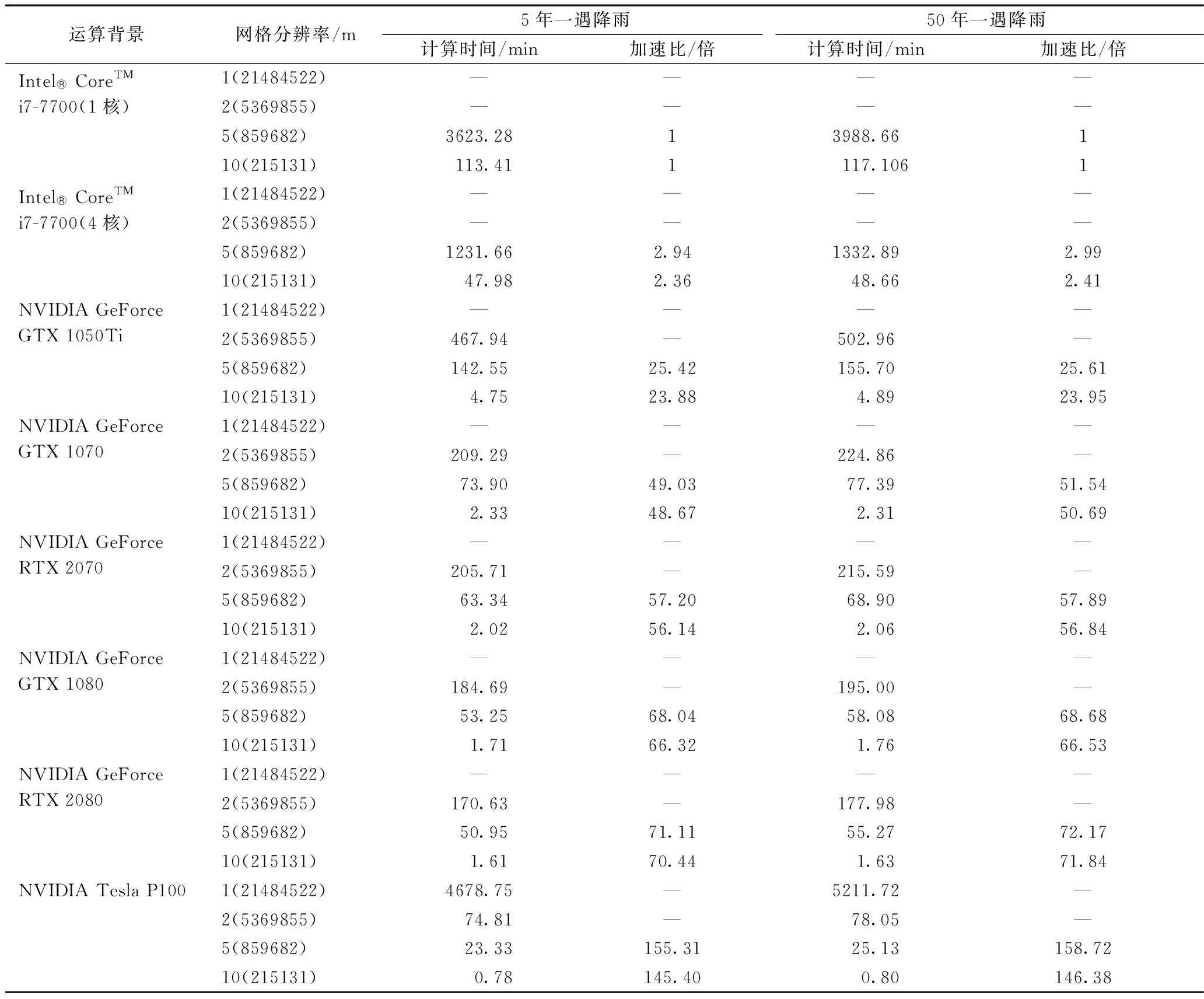
运算背景网格分辨率/m5年一遇降雨50年一遇降雨计算时间/min加速比/倍计算时间/min加速比/倍Intel CoreTMi7-7700(1核)1(21484522)————2(5369855)————5(859682)3623.2813988.66110(215131)113.411117.1061Intel CoreTMi7-7700(4核)1(21484522)————2(5369855)————5(859682)1231.662.941332.892.9910(215131)47.982.3648.662.41NVIDIA GeForce GTX 1050Ti1(21484522)————2(5369855)467.94—502.96—5(859682)142.5525.42155.7025.6110(215131)4.7523.884.8923.95NVIDIA GeForce GTX 10701(21484522)————2(5369855)209.29—224.86—5(859682)73.9049.0377.3951.5410(215131)2.3348.672.3150.69NVIDIA GeForce RTX 20701(21484522)————2(5369855)205.71—215.59—5(859682)63.3457.2068.9057.8910(215131)2.0256.142.0656.84NVIDIA GeForce GTX 10801(21484522)————2(5369855)184.69—195.00—5(859682)53.2568.0458.0868.6810(215131)1.7166.321.7666.53NVIDIA GeForce RTX 20801(21484522)————2(5369855)170.63—177.98—5(859682)50.9571.1155.2772.1710(215131)1.6170.441.6371.84NVIDIA Tesla P1001(21484522)4678.75—5211.72—2(5369855)74.81—78.05—5(859682)23.33155.3125.13158.7210(215131)0.78145.400.80146.38
注:“—”表示网格数超过设备的计算上限。
同一情形运算下可知,重现期为5年和50年时,降雨重现期越长,提速比越大,GPU计算效率越显著。在同一下垫面情况下,由于设计降雨重现期的变长,城市地表积水及径流量增加,导致计算量进一步增加,GPU对此适应性更强,因此,50年一遇降雨的计算效率高于5年一遇降雨。如情形3 NVIDIA GeForce GTX 1070计算前提下,5年和50年重现期提速比分别为49.03,51.54倍,50年重现期相对于5年重现期提升了约5.12%。
各重现期下,GPU在大尺度网格下计算效率相对更高。由于DEM网格分辨率的提高,城市地形能够准确反映地表微观特征,地表水流更加复杂,GPU的计算性能可以在此得到进一步体现。因此,随着DEM网格分辨率增大,计算效率进一步提高。如50年重现期NVIDIA Tesla P100计算前提下,情形三较Intel®CoreTMi7-7700(1核)提速比为158.72倍,情形四较Intel®CoreTMi7-7700(1核)提速比则为146.38倍,情形3相较于情形4提升了约8.43%。图6、7分别为不同重现期和计算情形下,计算时间图与GPU作为模拟计算平台相对于CPU作为模拟计算平台的提速比。
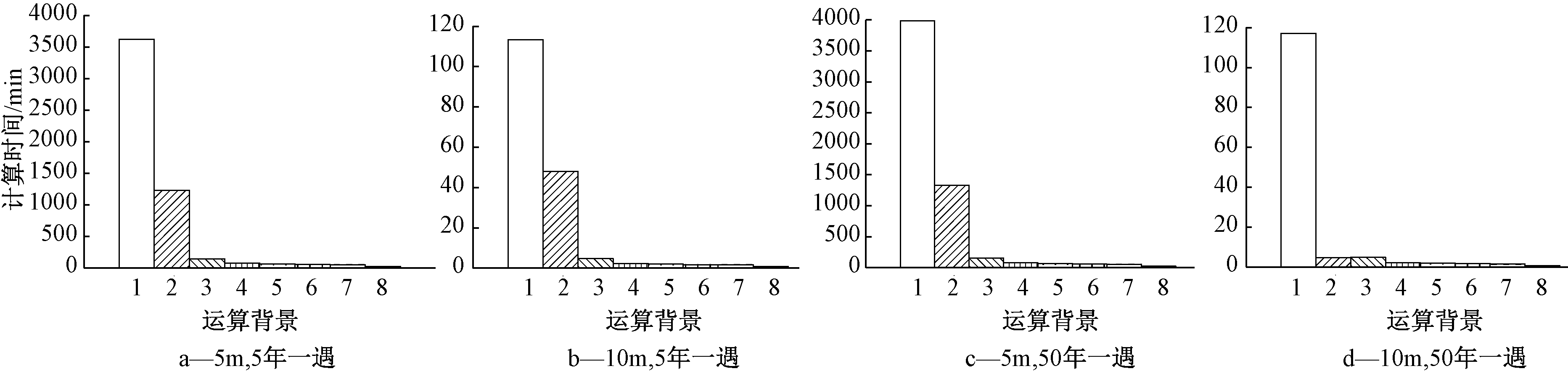
1—CPU(1核); 2—CPU(4核); 3—GTX 1050Ti; 4—GTX 1070; 5—RTX 2070; 6—GTX 1080; 7—RTX 2080; 8—Tesla P100。
图6 典型城市不同重现期降雨计算时间对比
Figure 6 Simulation run-times with different design hyetograph in typical cities
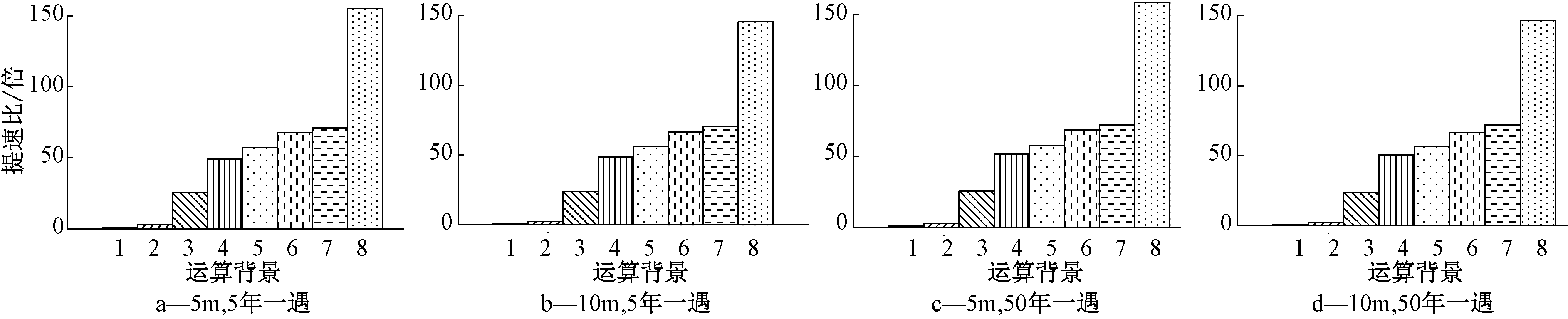
1—CPU(1核); 2—CPU(4核); 3—GTX 1050Ti; 4—GTX 1070; 5—RTX 2070; 6—GTX 1080; 7—RTX 2080; 8—Tesla P100。
图7 典型城市不同重现期降雨计算提速比对比
Figure 7 Acceleration ratios of GPU to CPU on different design hyetograph in typical cities
4 结 论
本文将GPU加速计算技术应用到典型城市雨洪过程数值模拟过程中,量化分析了CPU及不同GPU的计算性能。结果表明,GPU并行计算技术可使城市雨洪模型计算效率大大提升,且得到以下结论:
1)在城市雨洪数值模拟中,GPU相对于CPU提速明显,且可实现大尺度高效模拟计算;不同GPU加速效果不同,考虑所有GPU类型,其相对Intel®CoreTMi7-7700(1核)提速效果可达23.88~158.72倍。
2)在城市雨洪过程模拟中,50年降雨重现期计算效率较5年提高了0.29%~5.12%;对于重现期为5年和50年,降雨重现期越长,GPU计算效率越显著。
3)在城市雨洪模拟中,情形3CPU的计算效率比情形4(网格分辨率提升4倍)提高了0.76%~8.43%,即随着地形网格分辨率的增加,GPU的计算性能优势更加明显。
对于显式格式有限体积框架的城市雨洪模型,应用GPU技术可大大提升其计算效率。其中,水动力过程因其单网格计算量较水文过程更大,故其加速效果更为显著,且随着网格数量的增加,优势更为明显。因此,开展高分辨率城市雨洪过程模拟计算,GPU技术是理想的加速方法,可便捷实现高性能计算目标。考虑洪涝灾害预报的时效性要求,本研究成果对城市内涝快速预报及其他防灾减灾救灾工作具有一定指导意义。
[1] 周蕾, 吴先华, 吉中会. 考虑恢复力的洪涝灾害损失评估研究进展[J]. 自然灾害学报, 2017, 26(2): 11-21.
[2] CRED. EM-DAT, The International Disaster Database[EB/OL]. 2018.http://emdat.be/emdat_db/.
[3] 姜仁贵, 韩浩, 解建仓, 等. 变化环境下城市暴雨洪涝研究进展[J]. 水资源与水工程学报, 2016, 27(3): 11-17.
[4] 王志力, 耿艳芬, 金生. 具有复杂计算域和地形的二维浅水流动数值模拟[J]. 水利学报, 2005,36(4):439-444.
[5] 苑希民, 田福昌, 王丽娜. 漫溃堤洪水联算全二维水动力模型及应用[J]. 水科学进展, 2015, 26(1):83-90.
[6] NEAL J C, FEWTRELL T J, BATES P D, et al. A comparison of three parallelisation methods for 2D flood inundation models[J]. Environmental Modelling & Software, 2010, 25(4):398-411.
[7] SHARMA A K, LOCKE B R, FINNEY W C. A preliminary study of pulsed streamer corona discharge for the degradation of phenolin aqueous solutions[J]. Hazardous Waste and Hazardous Material,1993,10(2):209-219.
[8] LACASTA A, MORALES-HERNáNDEZ, M, MURILLO J, et al. An optimized GPU implementation of a 2D free surface simulation model on unstructured meshes[J]. Advances in Engineering Software, 2014, 78:1-15.
[9] 赵旭东, 赵杨, 孙家文, 等. 基于GPU加速的潮流模型及其在岛群二维水动力数值模拟中的应用[J]. 海洋环境科学, 2017, 36(5): 781-790.
[10] LIANG Q H, SMITH L S. A high-performance integrated hydrodynamic modelling system for urban flood simulations[J]. Journal of Hydroinformatics, 2015, 17(4): 518-533.
[11] 侯精明, 王润, 李国栋, 等. 基于动力波法的高效高尺度城市雨洪过程数值模型[J]. 水力发电学报, 2018, 37(3): 40-49.
[12] 李东来, 侯精明, 王新宏, 等. 河床冲淤对洪水演进影响数值模拟研究[J].泥沙研究,2018,43(5):13-20.
[13] 侯精明, 李桂伊, 李国栋, 等. 高效高精度水动力模型在洪水演进中的应用研究[J]. 水力发电学报, 2018, 37(2): 96-107.
[14] 刘菲菲, 侯精明, 郭凯华, 等. 基于全水动力模型的流域雨洪过程数值模拟[J]. 水动力学研究与进展(A辑), 2018, 33(6): 778-785.
[15] HOU J M, LIANG Q H, SIMONS F, et al. A stable 2D unstructured shallow flow model for simulations of wetting and drying over rough terrains[J]. Computers & Fluids, 2013, 82(17):132-147.
[16] YU C S, DUAN J. Two-dimensional depth-averaged finite volume model for unsteady turbulent flow[J]. Journal of Hydraulic Research, 2012, 50(6):599-611.
[17] SIVAKUMAR P, HYAMS D G, TAYLOR L K, et al. A primitive-variable Riemann method for solution of the shallow water equations with wetting and drying[J]. Journal of Computational Physics, 2009, 228(19):7452-7472.
[18] HOU J M, LIANG Q H, SIMONS F, et al. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment[J]. Advances in Water Resources, 2013, 52(2):107-131.
[19] LIANG Q H, MARCHE F. Numerical resolution of well-balanced shallow water equations with complex source terms[J]. Advances in Water Resources, 2009, 32(6):873-884.
[20] HUBBARD M E. Multidimensional slope limiters for MUSCL-type finite volume schemes on unstructured grids[J]. Journal of Computational Physics, 1999, 155(1):54-74.
[21] 侯精明, 李东来, 王小军, 等. 建筑小区尺度下LID措施前期条件对径流调控效果影响模拟[J]. 水科学进展, 2019, 30(1): 45-55.
[22] 侯精明, 郭凯华, 王志力, 等. 设计暴雨雨型对城市内涝影响数值模拟[J]. 水科学进展, 2017, 28(6): 820-828.