0 引 言
海绵城市建设为中国城市现代雨水控制利用与管理系统的发展提供了机遇，但同时也带来了极大挑战与困惑[1]。雨水溢流设施的计算与设计是雨水系统设计的重要环节之一。雨水口是雨水排水系统中收集地表水流的构筑物，是地面径流与管道排水的过渡点[2]，也是下沉式绿地等雨水设施在蓄满后溢流进入地表水体的主要通道，其水力特性对下沉式绿地的渗蓄能力有较大影响。
国外现行的雨水手册中，认为在堰流状态下，溢流口的过流状态类似薄壁堰，但其给出的设计公式较为粗糙，没有考虑不同溢流口内径以及溢流口设置高度的影响，在实际应用过程中将会产生较大误差。要系统研究溢流口水力特性，需从薄壁环形堰开始。在实际溢流过程中，环形薄壁堰类似于垂直排水管，但不同之处在于，环形薄壁堰在溢流后为自由出流，流量不受下游出流条件影响。BINNIE等[3]研究了涉及可变管长和固定直径的垂直溢流管，观察到3种流态：1)环形流动，出水管中央存在气芯，出水水流紧贴管壁；2)环形流动，出水管中央的气芯会偶尔闭合从而导致自由液面不再稳定；3)满管流并偶尔产生涡流的流动状态。KALINSKE等[4]把BINNIE的研究数据处理后拟合出式(1)，并将水头低于临界水头的流态称为部分满管流态，流量公式为:
Q=CKg0.5d0.5h2
(1)
式中：Q为过流流量，m3/s；g为重力加速度，m/s2；d为排水口直径，m；h为排水口前水深，即排水口外围，未显著受到排水影响的水深，m；CK为流量系数，无单位。显然这是一个量纲和谐的方程，但与堰流流量公式并不一致。
ANWAR等[5]研究了不同内径、高度的垂直出水管，并发现在堰流状态下，其流量系数是h/d 的递增函数，且与壁厚有关。Humphreys等[6]对具有不同入口条件的封闭溢洪道进行模型试验，同样发现流量系数与h/d 有一定关系，并提出在堰流状态下h-Q关系曲线可用式(2)表示。
Q=Cπdh3/2
(2)
式中：Q为过流流量，m3/s；d为排水口直径，m；h为排水口前水深，m；C为有量纲流量系数，此式显然是经验公式。
Banisoltan[7]将堰流状态下的h-Q曲线与式(3)进行比较，拟合出流量系数Cd的关系式如式(4)所示。
(3)
(4)
式中：Cd为流量系数，无单位，其余符号同前，这是一个量纲和谐的方程，且与堰流公式表达相近。
虽然垂直排水管的入口形状以及流态与环形薄壁堰有相似之处，但由于垂直排水管在出流过程中，受下游出流条件影响较大，其流量系数并不适合环形堰。本文对环形薄壁堰的水力特性进行了系统的试验研究，分析了现行计算公式的计算误差，研究了堰高对其水力特性的影响，并根据试验数据得到简单实用的计算公式。
1 试验装置与方法
试验装置如图1所示，水流由循环水库经水泵提升，经过闸阀流至方形槽内，用超声波流量计测量试验流量。方形槽内的水经矩形渠道进入圆形水箱底层，再经过布水装置进入水箱上层，布水装置为1个穿孔圆盘，距离水箱底部150 mm，水流进入水箱底部后经环向均布的开孔均匀进入上层水箱，再径向汇流，通过环形薄壁堰溢流。试验采用水位探针测量溢流高度即堰上水头。
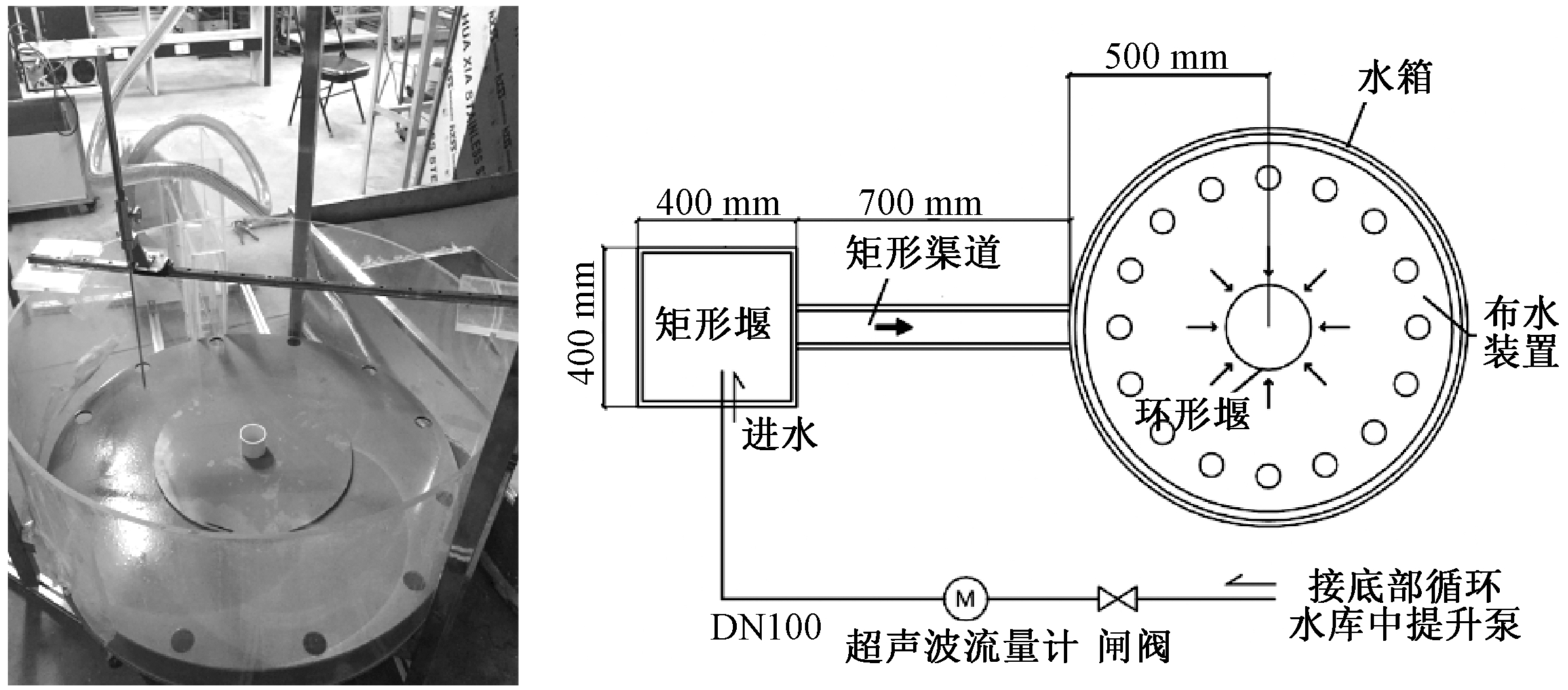
图1 环形薄壁堰溢流试验装置
Figure 1 Overflow experiment equipment of thin-annular weir
环形薄壁堰采用成型PVC管，用PVC管突出布水平板的长度表示环形薄壁堰的高度，根据不同的堰高将试验分为3个系列，分别记为H1、H2、H3，其管径即为环形薄壁堰的有效内径。堰高与内径尺寸组合如表1所示。
显然，环形薄壁堰发生自由溢流时，影响其水力特性的主要因素为堰高和内径。因此，试验分别在3种不同堰高工况下，获取不同内径下的流量-堰上水头关系。本试验只研究环形薄壁堰在堰流条件下的水力特性，装置试验流量为0～22 m3/h。试验过程中，流量由小到大，并测量每个流量所对应的堰上水头，每次改变流量后，静待10 min后进行观测，并在水位没有明显下降且相对稳定的位置测量堰上水头。由于布水平板距水箱底150 mm，故在H1系列的试验中，将长度为150 mm的PVC管同心安装在圆形水箱的底部，管顶与布水平板平齐，此时，环形薄壁堰的高度为0 mm。试验过程中，增加PVC管的长度即增加了堰高，由此H2、H3系列的堰高分别为60，120 mm。
表1 环形薄壁堰溢流实验参数
Table 1 The experimental parameters of thin-annular weir
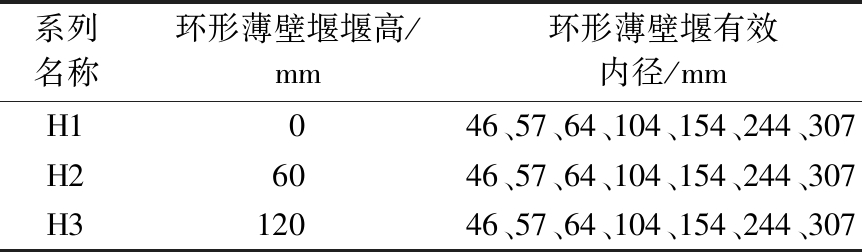
系列名称环形薄壁堰堰高/mm环形薄壁堰有效内径/mmH1046、57、64、104、154、244、307H26046、57、64、104、154、244、307H312046、57、64、104、154、244、307
2 结果与分析
2.1 堰上水头与流量的关系
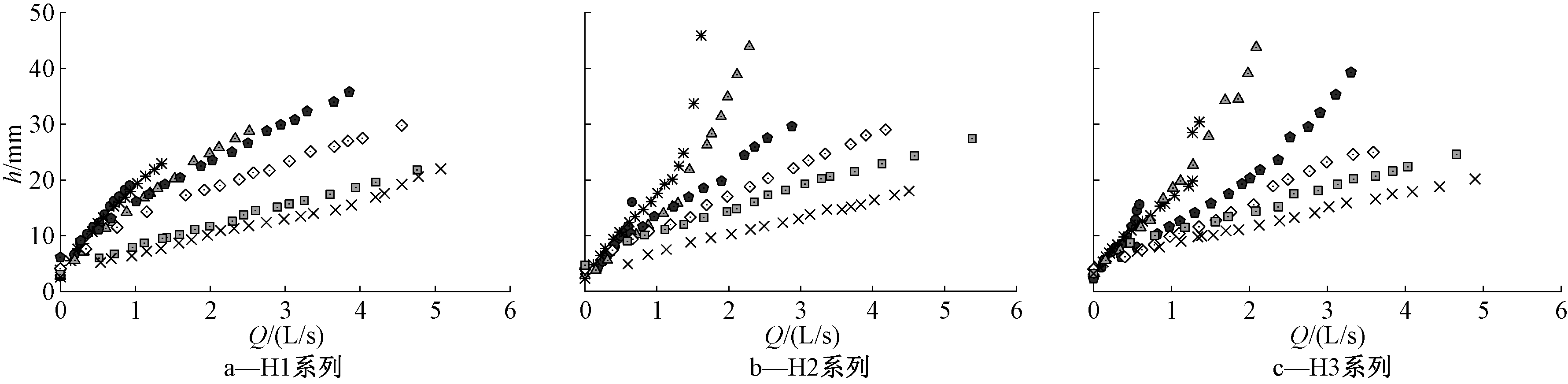
试验所得的h-Q曲线如图2所示。试验观察发现，在溢流流量较小时形成贴壁堰流，流量增大后，过堰水流在惯性作用下会脱壁形成自由出流。流量进一步加大，则由于径向流动的汇聚壅塞作用影响到出流能力，导致堰上水头随流量上升曲线出现拐点，并迅速上升。
d=46 mm；
d=57 mm；
d=64 mm；
d=104 mm；
d=154 mm；
d=244 mm；
d=307 mm。
图2 环形薄壁堰溢流的水头-流量关系
Figure 2 Head-discharge relation of thin-annular weir
2.2 现行溢流口计算公式对比分析
为了验证溢流口现行计算公式的准确性，将试验所得的数据结果与计算结果进行对比。以《昆士兰城市排水手册》[8]为例，在堰流状态下，溢流口的计算公式见式(5)：
Qc=BF1.66Lh3/2
(5)
式中：Qc为溢流流量，m3/s；BF为阻塞因子，无单位，在此只讨论环形薄壁堰的水力特性，不考虑雨水篦子形状等的影响因素，故BF=1；1.66为流量系数，无单位；L为堰长，即溢流口周长，m；h为堰上水头，m。
从式(5)可知：当BF和L值一定时，溢流流量只与堰上水头有关，但在实际溢流过程中，溢流口的内径对流量系数会有一定影响，且在不同堰高下，溢流时所产生的垂直收缩程度也不同，式(5)并没有反映出环形堰内径与堰高对其水力特性的影响。为评估式(5)的计算结果与实测数值的差别，将试验数据与公式计算结果进行对比，按式(6)计算其相对误差：
δ=(Qc-Q)/Q×100%
(6)
式中：δ为相对误差，%；Q为实测流量，m3/s。
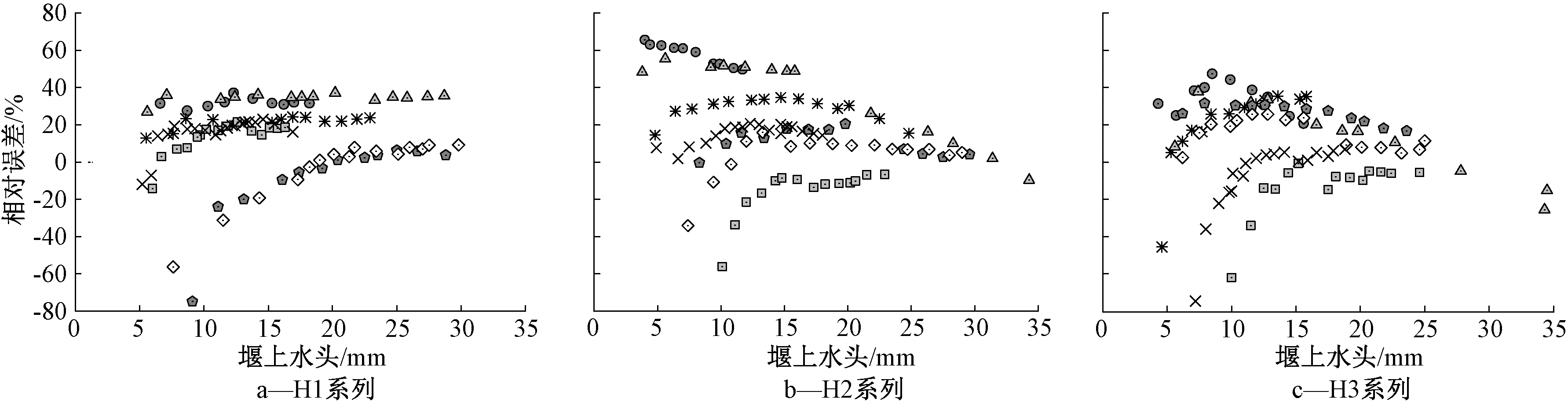
由图3可见，实测流量与式(5)计算流量之间具有较大差别，计算得到的大部分结果比实测值偏大，最大相对误差值为65%。故采用现行计算公式计算环形堰流量的精度并不能满足要求。
d=46 mm； d=57 mm； d=64 mm； d=104 mm； d=154 mm； d=244 mm； d=307 mm。
图3 堰上水头与相对误差之间的关系
Figure 3 Relation between weir head and relative error
2.3 拟合无量纲公式
无论是薄壁堰、宽顶堰还是实用堰，其过流能力计算均采用堰流基本计算式(7)[9]，区别在于流量系数C 的不同。
Qc=CLh3/2
(7)
式中：Qc为溢流流量，m3/s；h 为堰上水头，m；L为堰长，m；对环形薄壁堰来说，L=πd，d 为环形薄壁堰内径，m；C 可用CW(2 g)1/2代替，CW为无量纲流量系数，g为重力加速，m/s2，则有：
Qc=Cw(2g)1/2πdh3/2
(8)
为了减少试验中控制参数的个数，方便整理试验数据和经验公式，将堰流基本计算式转化为无量纲方程。在环形薄壁堰的溢流过程中，由于其水力特性主要受到惯性力和重力影响，故以弗劳德数为无量纲变量来拟合无量纲关系式，以直径d为特征长度，以过流断面平均速度v为特征速度，过流弗劳德数FD为：
(9)
式中：A为特征面积，可用d2替代，g为重力加速度，为贴近堰流公式表达，以2g取代g，则式(9)变为：
(10)
将式(8)带入式(10)，得到无量纲关系式：
(11)
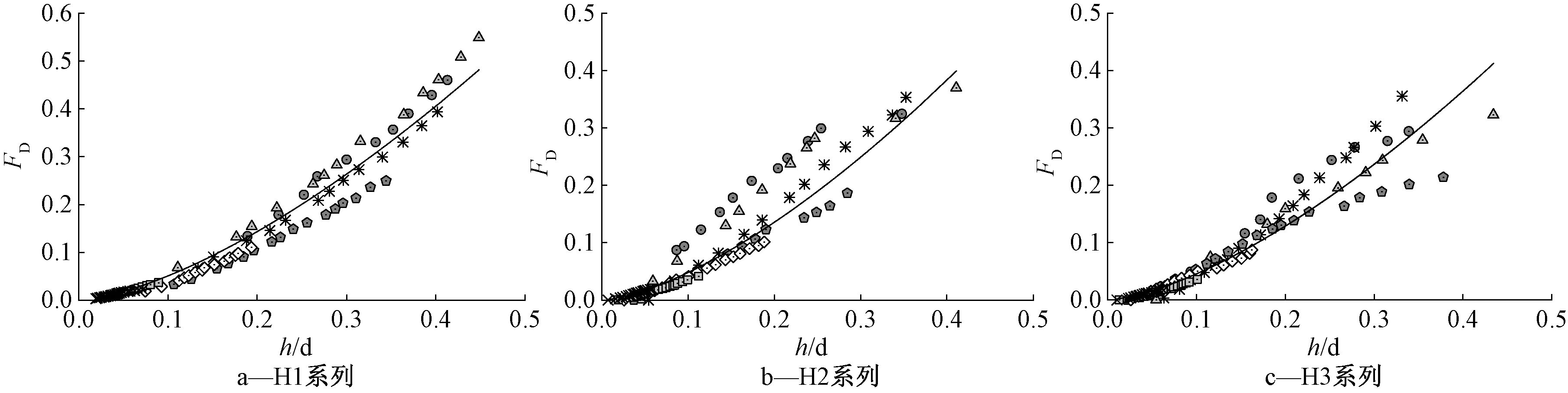
根据式(11)得到H1、H2和H3系列的 FD～h/d 关系，并对试验结果进行拟合，拟合结果如图4所示。H1、H2和H3系列的拟合公式如式(12)—(14)所示，分别对应堰高为0，60，120 mm时的弗劳德数，相关系数R2分别为0.9658、0.8734和0.908。从拟合结果的相关系数可以看出，FD与 h/d 之间存在较为稳定的函数关系。
(12)
(13)
(14)
d=46 mm； d=57 mm； d=64 mm； d=104 mm； d=154 mm； d=244 mm； d=307 mm； ——拟合曲线。
图4 参数FD与h/d关系曲线
Figure 4 Relation curve between parameter FD and h/d
由图4可以看出：当堰上水头相对较小时，不同直径下数据吻合度较高，因为此时径向汇流速度较小，汇聚产生的壅塞以及出流压强变化的影响没有显现出来；而在堰上水头相对较高的情况下，数据随直径不同较为离散，径向汇流对不同直径堰出流的影响才得已显现。
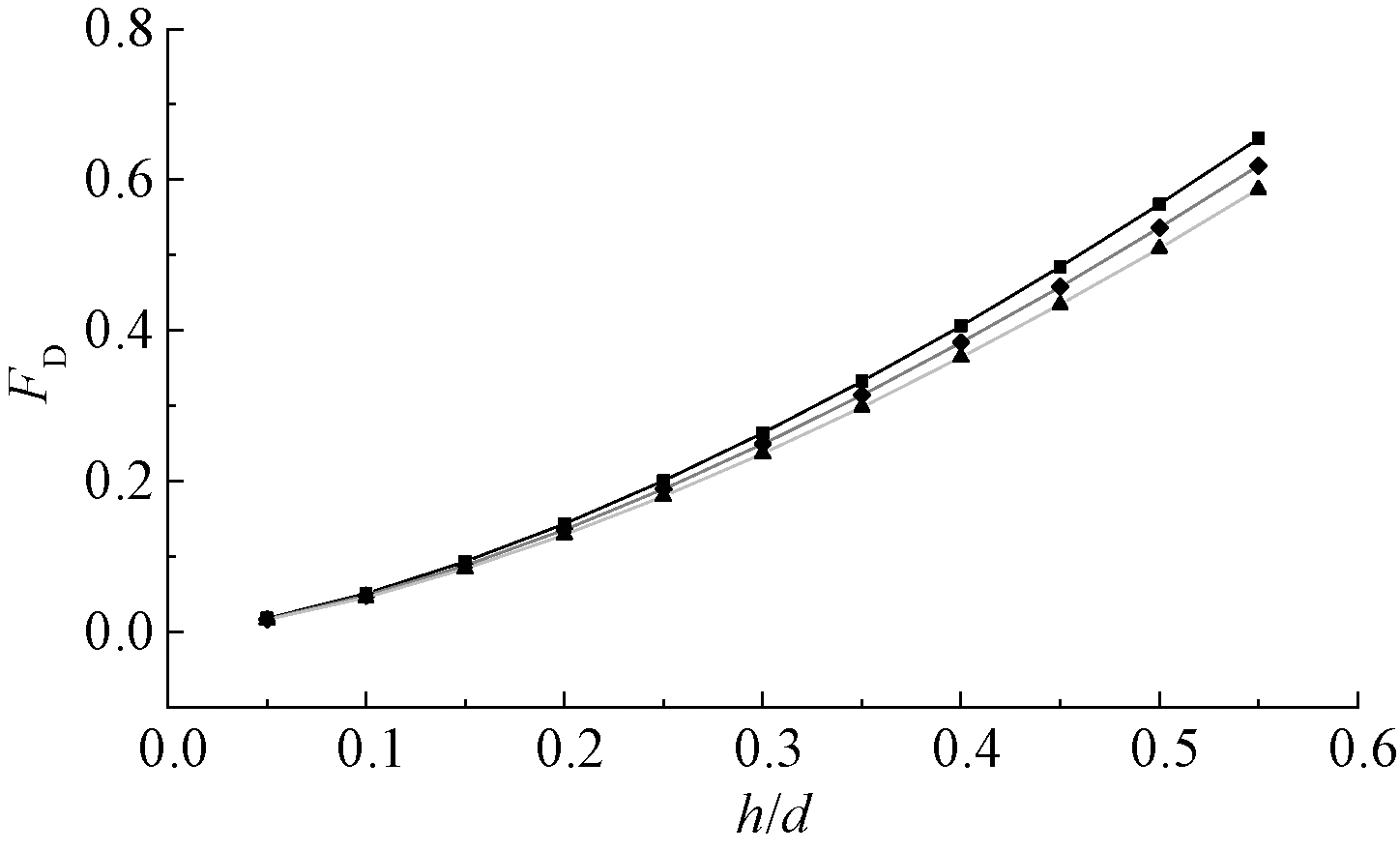
图5为不同堰高下的FD-h/d拟合关系，可见一定范围内堰高越高，相同FD对应的h/d越高，即相同流量下，其对应的堰上水头越高。这和其他薄壁堰的情况类似，是过堰水流发生向上收缩导致的，随堰高升高，会逐渐达到“充分收缩”，堰高带来的影响也将随之减弱直至消失，但对海绵设施溢流口而言，过高的堰高无实际意义。实际使用式(11)—(14)进行计算时，可按堰高0，60，120 mm代入相关数据，堰高不吻合时，可进行插值处理。
—H1； 
—H2； 
—H3。
图5 不同堰高下参数FD与h/d拟合关系曲线对比
Figure 5 Comparison of fitting curve between parameter FD and h/d under different the height of weir
3 结 论
通过模型实验系统研究了环形薄壁堰出流，实验数据表明，环形薄壁不同堰高条件下水力特性存在差异，在溢流流量相同的条件下，堰高越高，其对应的水头高度越高，这与直堰的基本规律一致。
通过对不同堰高、内径的环形薄壁堰水力特性的分析，根据试验结果，给出不同堰高下的环形薄壁的计算公式，即式(11)—(14)，可为雨水系统中溢流口的设计计算提供参考。
[1] 李俊奇,王文亮.基于多目标的城市雨水系统构建与展望[J].给水排水,2015,51(4):1-3，37.
[2] 姚飞骏.雨水口的流量计算方法探讨[J].中国给水排水,2013,29(14):45-48.
[3] BINNIE A M. The use of a vertical pipe as an overflow for a large tank[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1938, 168(933):219-237.
[4] KALINSKE A A. Hydraulics of vertical drain and overflow pipes. Iowa City, IA: Iowa Institute of Hydraulic Research, 1940.
[5] ANWAR H O. Coefficients of discharge for gravity flow into vertical pipes[J]. J Hydraul Res,1965, 3 (1): 1-19.
[6] HUMPHREYS H W, SIGURDSSON G, OWEN H J. Model test results of circular, square and rectangular forms of drop-inlet entrance to closed-conduit spillways[R]. Report of Investigation No. 65. Champaign, IL: Illinois State Water Survey,1970.
[7] BANISOLTAN S, RAJARATNAM N, ZHU D Z. Experimental and theoretical investigation of vertical drains with radial inflow[J]. J Hydraul Eng, 2016,143 (5): 04016103.
[8] Department of Environmental and Resource Management (DERM). Queensland Urban Drainage Manual (QUDM)[M]. second ed. Queensland: Queensland Government,2007.
[9] 李稳坐,邱勇,尹韬,等.基于堰流基本公式的W型迷宫堰过流能力拟合分析[J].人民珠江,2017,38(7):69-72.